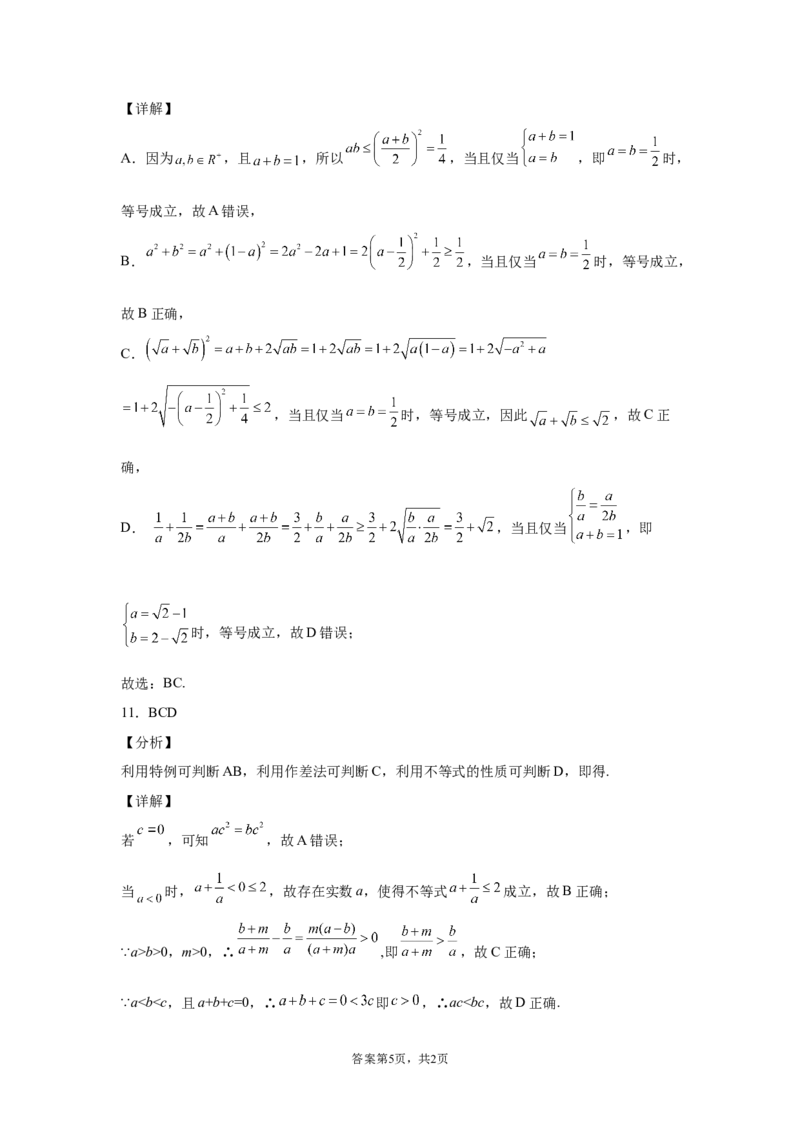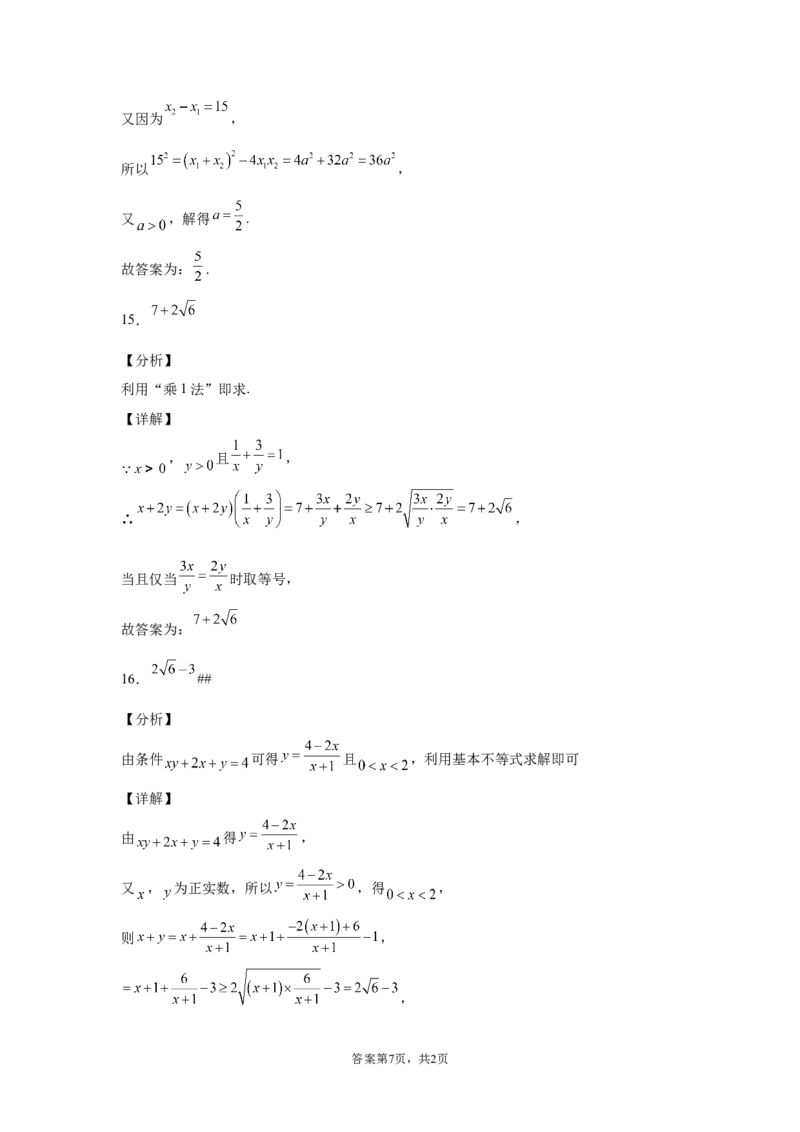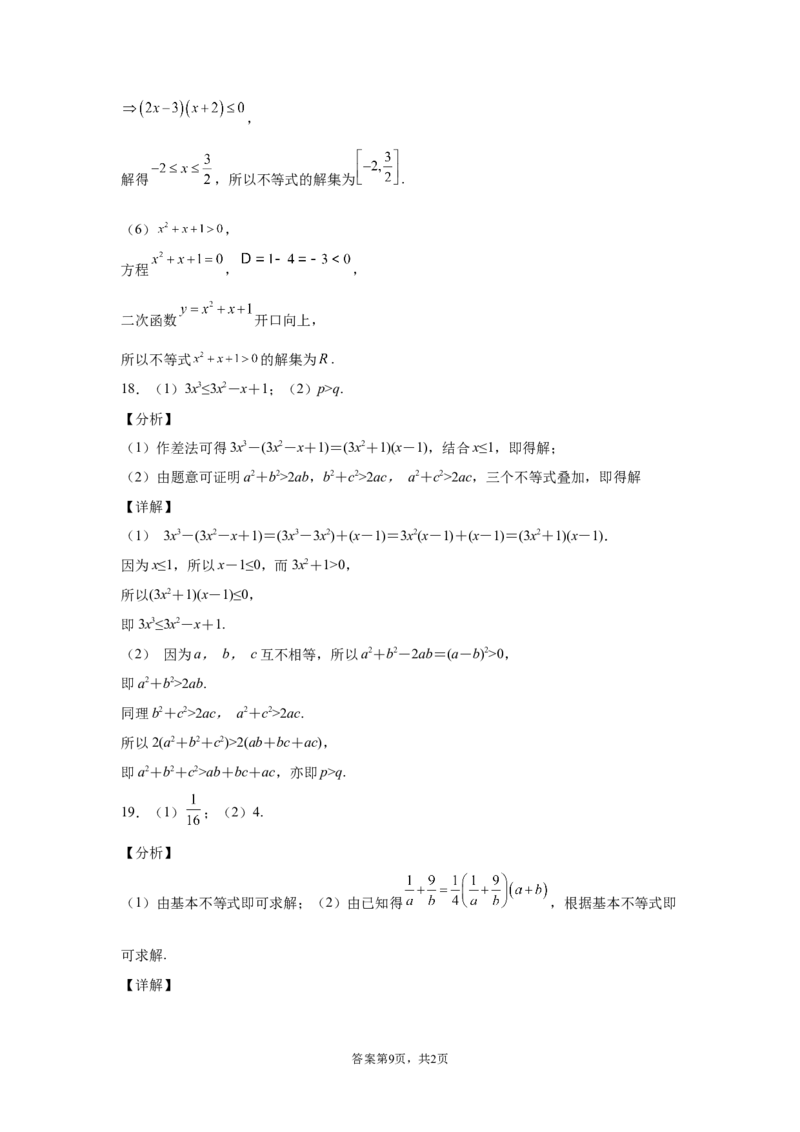文档内容
第二章 一元二次函数、方程和不等式同步测试卷
一、单选题
1.不等式 的解集是( )
A. B.
C. 或 D.
2.函数 取得最小值时的自变量x等于( )
A. B. C.1 D.3
3.已知不等式 解集为 ,下列结论正确的是( )
A. B.
C. D.
4.已知P=a2+ (a≠0),Q=b2-4b+7(1<b≤3).则P、Q的大小关系为( )
A.P>Q B.P<Q C.P≥Q D.P≤Q
5.当0b,则 B.存在实数a,使得不等式 成
立
C.若a>b>0,m>0,则 D.若a”或“<”填空)
14.若关于x的不等式 ( )的解集为 ,且
试卷第2页,共3页,则a的值为___________.
15.已知x>0,y>0,且 ,则x+2y的最小值为___________.
16.已知正实数x,y满足 ,则 的最小值为___________.
四、解答题
17.解下列不等式:
(1) ; (2) ;
(3) ; (4) ;
(5) ; (6) .
18.(1)已知x≤1,比较3x3与3x2-x+1的大小.
(2)已知a,b,c是两两不等的实数,p=a2+b2+c2,q=ab+bc+ca,试比较p与q
的大小.
19.(1)已知 , ,且 ,求 的最大值;
(2)若 , ,且 ,求 的最小值.
20.(1)求函数 的最小值;
(2)已知 且 ,求x+y的最小值.
21.(1)k是什么实数时,方程 有两个不相等的实数根?
(2)已知不等式 对一切实数x恒成立,求实数k的取值范围.
22.(1)若关于x的不等式x2-x+1>2x+m在[-1, 1]上恒成立,求实数m的取值范
围;
(2)若关于x的不等式x2-x+1>2x+m在[-1, 1]上有解,求实数m的取值范围.
试卷第3页,共3页第二章 一元二次函数、方程和不等式同步测试卷答案
1.B
【分析】
将分式不等式化为一元二次不等式求解即可.
【详解】
解:∵ ,∴
∴ ,即 ,∴ ,解得
故选:B
2.A
【分析】
根据基本不等式确定函数 取得最小值时的自变量x的值.
【详解】
函数 ,且 ,可得 ,当且仅当 ,即
时,取得最小值 .
故选:A.
3.C
【分析】
根据不等式 解集为 ,得方程 的解为 或 ,
且 ,利用韦达定理即可将 用 表示,即可判断各选项的正误.
【详解】
解:因为不等式 解集为 ,
答案第1页,共2页所以方程 的解为 或 ,且 ,
所以 ,所以 ,
所以 ,故ABD错误;
,故C正确.
故选:C.
4.C
【分析】
由基本不等式可得 ,通过配方结合 可得 即可选得答案.
【详解】
,当且仅当 时等号成立,
,当 时等号成立,
所以 .
故选:C
5.B
【分析】
利用基本不等式求解.
【详解】
因为0b>0,m>0,∴ ,即 ,故C正确;
∵a
【分析】
利用作差法即得.
【详解】
∵ ,
∴ > .
故答案为:>
14.
【分析】
根据一元二次不等式的解集与对应方程解的关系,利用根与系数的关系,结合题意即可求
出a的值.
【详解】
解:关于x的不等式 ( )的解集为 ,
所以 , 是一元二次方程 的实数根,
所以 ,且 , .
答案第6页,共2页又因为 ,
所以 ,
又 ,解得 .
故答案为: .
15.
【分析】
利用“乘1法”即求.
【详解】
, 且 ,
∴ ,
当且仅当 时取等号,
故答案为:
16. ##
【分析】
由条件 可得 且 ,利用基本不等式求解即可
【详解】
由 得 ,
又 , 为正实数,所以 ,得 ,
则 ,
,
答案第7页,共2页当且仅当 ,即 时取等号,
所以 的最小值为 ,
故答案为:
17.(1) ;(2) ;(3) ;(4) ;(5)
;(6)
【分析】
利用一元二次不等式的解法即可求解.
【详解】
(1) ,
所以不等式的解集为 .
(2) 或 ,
所以不等式的解集为 .
(3) ,
解得 ,
所以不等式的解集为 .
(4) ,
解得 或 ,
所以不等式的解集为 .
(5)
答案第8页,共2页,
解得 ,所以不等式的解集为 .
(6) ,
方程 , ,
二次函数 开口向上,
所以不等式 的解集为 .
18.(1)3x3≤3x2-x+1;(2)p>q.
【分析】
(1)作差法可得3x3-(3x2-x+1)=(3x2+1)(x-1),结合x≤1,即得解;
(2)由题意可证明a2+b2>2ab,b2+c2>2ac, a2+c2>2ac,三个不等式叠加,即得解
【详解】
(1) 3x3-(3x2-x+1)=(3x3-3x2)+(x-1)=3x2(x-1)+(x-1)=(3x2+1)(x-1).
因为x≤1,所以x-1≤0,而3x2+1>0,
所以(3x2+1)(x-1)≤0,
即3x3≤3x2-x+1.
(2) 因为a, b, c互不相等,所以a2+b2-2ab=(a-b)2>0,
即a2+b2>2ab.
同理b2+c2>2ac, a2+c2>2ac.
所以2(a2+b2+c2)>2(ab+bc+ac),
即a2+b2+c2>ab+bc+ac,亦即p>q.
19.(1) ;(2)4.
【分析】
(1)由基本不等式即可求解;(2)由已知得 ,根据基本不等式即
可求解.
【详解】
答案第9页,共2页(1)因为 , ,且 ,所以 ,
当且仅当 ,即 时,等号成立,
所以 ,
所以 ,
故 的最大值为 .
(2)因为 , ,且 ,所以
,
当且仅当 ,即 时,等号成立,
所以 的最小值为4.
20.(1)5;(2)16.
【分析】
(1)构造 ,利用均值不等式,即得解
(2)构造 ,利用均值不等式,即得解
【详解】
(1) ,
又 ,
.
当且仅当 ,即x=4时,y有最小值5.
答案第10页,共2页(2) ,
,
当且仅当 ,又 ,
即x=4,y=12时,上式取等号.
故当x=4,y=12时, .
21.(1) ;(2) 或 .
【分析】
结合二次不等式和二次函数之间的关系得出关于 的不等式,从而求出 的范围.
【详解】
(1)方程 有两个不相等的实数根,即 ,
则有 ,
即 ,
,即 ,解得 ;
(2)不等式 对一切实数x恒成立,
即 ,那么 ,那么 ,即 或 .
22.(1){m|m<-1};(2){m|m<5}.
【分析】
先参变分离,转化为m<x2-3x+1,(1)恒成立问题,只需m小于函数y=x2-3x+1的
最小值;(2)有解问题,只需m小于函数y= x2-3x+1的最大值.
【详解】
解 (1) x2-x+1>2x+m在[-1, 1]上恒成立,
即m<x2-3x+1在[-1, 1]上恒成立.
答案第11页,共2页令y=x2-3x+1= ,
则当-1≤x≤1时,y随x的增大而减小,
所以y =12-3×1+1=-1,
min
所以实数m的取值范围是{m|m<-1}.
(2) x2-x+1>2x+m在[-1, 1]上有解,
即m<x2-3x+1在[-1, 1]上有解.
令y=x2-3x+1= ,
则当-1≤x≤1时,y随x的增大而减小,
所以y =(-1)2-3×(-1)+1=5,
max
所以实数m的取值范围是{m|m<5}.
答案第12页,共2页答案第13页,共2页