2006年重庆高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_重庆

2006 年重庆高考文科数学真题及答案 注意事项： 1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。 2．答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。如需改动，用橡皮 檫擦干净后，在选涂其他答案标号。 3．答非选择题时，必须用0.5mm黑色签字笔，将答案书写在答题卡规定的位置上。 4．所有题目必须在答题卡上作答，在试卷上答题无效。 5．考试结束后，将试题卷和答题卡一并交回。 参考公式： 如果事件A、B互斥，那么P(AB) P(A)P(B) 如果事件A、B相互独立，那么P(A B) P(A) P(B)   如果事件A在一次试验中发生的概率是 p，那么n次独立重复试验中恰好发生k次的概率： P (k)Ckpk(1 p)nk n n 一．选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个备选项中，只 有一项是符合题目要求的。 （1）已知集合U {1,2,3,4,5,6,7}，A{2,4,5,7}，B{3,4,5}，则(ð A) (ð B) U  U （A）{1,6} （B）{4,5} （C）{2,3,4,5,7} （D）{1,2,3,6,7} （2）在等差数列a 中，若a 0且a a 64，a 的值为 n n 3 7 5 （A）2 （B）4 （C）6 （D）8 （3）以点（2，－1）为圆心且与直线3x4y50相切的圆的方程为 （A）(x2)2 (y1)2 3 （B）(x2)2 (y1)2 3 （C）(x2)2 (y1)2 9 （D）(x2)2 (y1)2 3 （4）若P是平面外一点，则下列命题正确的是 （A）过P只能作一条直线与平面相交 （B）过P可作无数条直线与平面垂直 （C）过P只能作一条直线与平面平行 （D）过P可作无数条直线与平面平行 （5）2x35 的展开式中x2的系数为 （A）－2160 （B）－1080 （C）1080 （D）2160 1 （6）设函数 y  f(x)的反函数为 y  f 1(x)，且 y  f(2x1)的图像过点( ,1)，则 2 y  f 1(x)的图像必过 第1页 | 共10页1 1 （A）( ,1) （B）(1, ) （C）(1,0) （D）(0,1) 2 2 （7）某地区有300家商店，其中大型商店有30家，中型商店有75家，小型商店有195家。 为了掌握各商店的营业情况，要从中抽取一个容量为20的样本。若采用分层抽样的方法， 抽取的中型商店数是 （A）2 （B）3 （C）5 （D）13     （8）已知三点A(2,3),B(1,1),C(6,k)，其中k为常数。若 AB  AC ，则AB与AC 的夹角为 24  24 （A）arccos( ) （B） 或arccos 25 2 25 24  24 （C）arccos （D） 或arccos 25 2 25 （9）高三（一）班学要安排毕业晚会的4各音乐节目，2个舞蹈节目和1个曲艺节目的演 出顺序，要求两个舞蹈节目不连排，则不同排法的种数是 （A）1800 （B）3600 （C）4320 （D）5040   3  1 （10）若,(0, )，cos( ) ,sin( ) ，则cos()的值等于 2 2 2 2 2 3 1 1 3 （A） （B） （C） （D） 2 2 2 2 9 x2 y2 （11）设A(x ,y ),B(4, ),C(x ,y )是右焦点为F 的椭圆  1上三个不同的点， 1 1 5 2 2 25 9 则“ AF , BF , CF 成等差数列”是“x x 8”的 1 2 （A）充要条件 （B）必要不充分条件 （C）充分不必要条件 （D）既非充分也非必要 （12）若a,b,c0且a2 2ab2ac4bc12，则abc的最小值是 （A）2 3 （B）3 （C）2 （D） 3 二．填空题：本大题共4小题，每小题4分，共24分。把答案填写在答题卡相应位置上。 2 5  （13）已知sin ， ，则tan 。 5 2 （14）在数列{a }中，若a 1，a a 2(n1)，则该数列的通项a  。 n 1 n1 n n （15）设a0,a1，函数 f(x)log (x2 2x3)有最小值，则不等式log (x1)0 a a 的解集为 。 第2页 | 共10页x2y30  （16）已知变量x，y满足约束条件x3y30。若目标函数z ax y（其中a 0）  y10  仅在点(3,0)处取得最大值，则a的取值范围为 。 三．解答题：本大题共6小题，共76分。解答应写出文字说明、证明过程或演算步骤。 （17）（本小题满分13分） 甲、乙、丙三人在同一办公室工作。办公室只有一部电话机，设经过该机打进的电话是打给 1 1 1 甲、乙、丙的概率依次为 、 、 。若在一段时间内打进三个电话，且各个电话相互独 6 3 2 立。求： （Ⅰ）这三个电话是打给同一个人的概率； （Ⅱ）这三个电话中恰有两个是打给甲的概率； （18）（本小题满分13分） 设函数 f(x) 3cos2xsinxcosxa（其中0,aR）。且 f(x)的图像在 y  轴右侧的第一个最高点的横坐标是 。 6 （Ⅰ）求的值；  5 （Ⅱ）如果 f(x)在区间[ , ]上的最小值为 3，求a的值； 3 6 （19）（本小题满分12分） 设函数 f(x) x3 3ax2 3bx的图像与直线12x y10相切于点(1,11)。 （Ⅰ）求a,b的值； （Ⅱ）讨论函数 f(x)的单调性。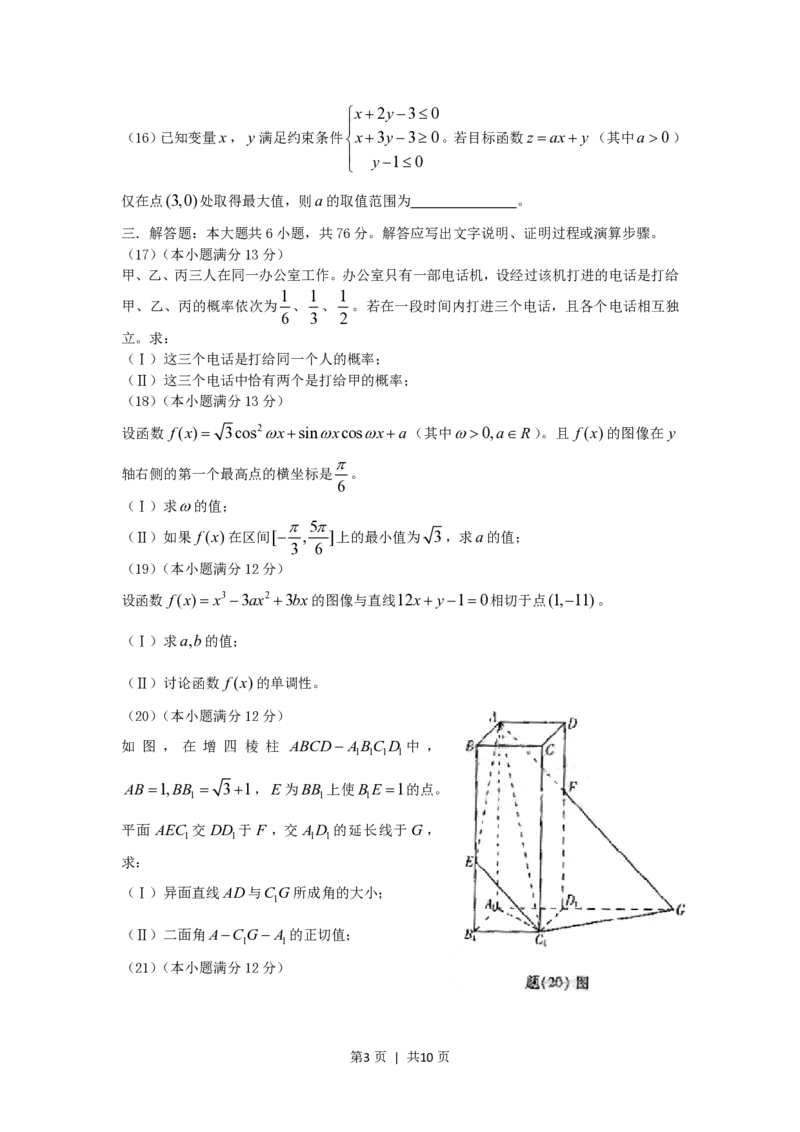 （20）（本小题满分12分） 如 图 ， 在 增 四 棱 柱 ABCDABC D 中 ， 1 1 1 1 AB1,BB  31，E为BB 上使BE 1的点。 1 1 1 平面 AEC 交 DD 于 F ，交 AD 的延长线于G， 1 1 1 1 求： （Ⅰ）异面直线AD与CG所成角的大小； 1 （Ⅱ）二面角ACGA 的正切值； 1 1 （21）（本小题满分12分） 第3页 | 共10页2x b 已知定义域为R的函数 f(x) 是奇函数。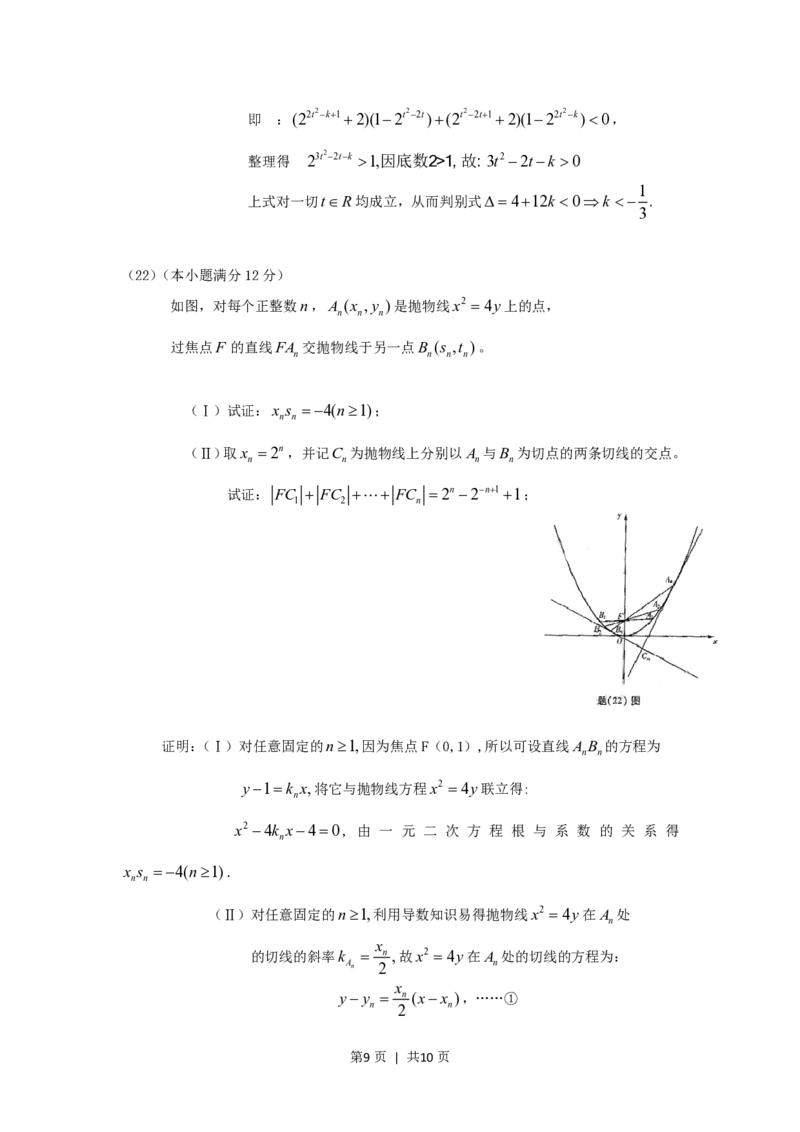 2x1a （Ⅰ）求a,b的值； （Ⅱ）若对任意的tR，不等式 f(t2 2t) f(2t2 k)0恒成立，求k的取值范围； （22）（本小题满分12分） 如图，对每个正整数n，A (x ,y )是抛物线x2 4y上的点， n n n 过焦点F 的直线FA 角抛物线于另一点B (s ,t )。 n n n n （Ⅰ）试证：x s 4(n1)； n n （Ⅱ）取x 2n，并记C 为抛物线上分别以 A 与B 为切 n n n n 点 的 两 条 切 线 的 交 点 。 试 证 ： FC  FC   FC 2n 2n11； 1 2  n 2006年重庆高考文科数学真题参考答案 一．选择题 1.D 2.D 3.C 4.D 5.B 6.C 7.C 8.D 9.B 10.B 11.A 12.A 二．填空题 1 (13) -2 (14) 2n – 1 (15)（2，） （16）a 2 三．解答题 （17）（本小题满分13分）甲、乙、丙三人在同一办公室工作。办公室只有一部电话机，设 1 1 1 经过该机打进的电话是打给甲、乙、丙的概率依次为 、 、 。若在一段时间 6 3 2 内打进三个电话，且各个电话相互独立。求： （Ⅰ）这三个电话是打给同一个人的概率； （Ⅱ）这三个电话中恰有两个是打给甲的概率； 解：（Ⅰ）由互斥事件有一个发生的概率公式和独立事件同时发生的概率公式， 1 1 1 1 所求概率为： p( )3( )3( )3  . 6 3 2 6 1 （Ⅱ）这是n=3，p= 的独立重复试验，故所求概率为： 6 1 5 5 P(2)C2( )2( ) . 3 3 6 6 72 （18）（本小题满分13分）设函数 f(x) 3cos2xsinxcosxa 第4页 | 共10页 （其中0,aR）。且 f(x)的图像在y轴右侧的第一个最高点的横坐标是 。 6 （Ⅰ）求的值；  5 （Ⅱ）如果 f(x)在区间[ , ]上的最小值为 3，求a的值； 3 6 3 1 3  3 解：（I） f(x) cos2x sin2x sin(2x ) a 2 2 2 3 2    1 依题意得 2    ． 6 3 2 2  3  5 （II）由（I）知， f(x)sin(x ) ．又当x[ , ]时， 3 2 3 6  7 1   π 5π x [0, ]，故 sin(x )1，从而 f(x)在区间  ，   3 6 2 3  3 6  1 3 31 上的最小值为 3   a，故a  . 2 2 2 （19）（本小题满分12分） 设函数 f(x) x3 3ax2 3bx的图像与直线12x y10相切于点(1,11)。 （Ⅰ）求a,b的值； （Ⅱ）讨论函数 f(x)的单调性。 解：（Ⅰ）求导得 f '(x)3x2 6ax3b。 由于 f(x)的图像与直线12x y10相切于点(1,11)， 所以 f(1)11, f '(1)12，即： 1-3a+3b = -11 解得: a1,b3． 3-6a+3b=-12 （ Ⅱ ） 由 a1,b3得 ： f '(x)3x2 6ax3b3(x2 2x3)3(x1)(x3) 令f′（x）＞0，解得 x＜-1或x＞3；又令f′（x）< 0，解得 -1＜x＜3. 故当x（, -1）时，f(x)是增函数，当 x（3,）时，f(x)也是增 函数， 但当x（-1 ，3）时，f(x)是减函数. 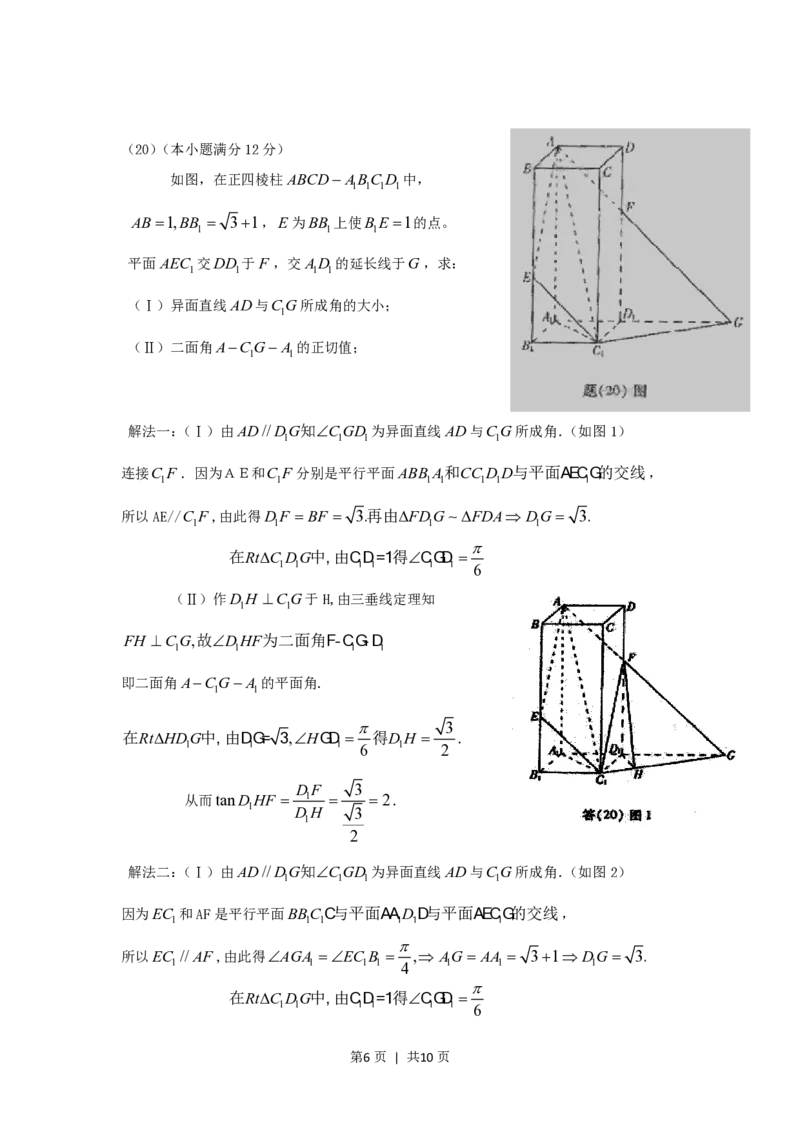第5页 | 共10页（20）（本小题满分12分） 如图，在正四棱柱ABCDABC D 中， 1 1 1 1 AB1,BB  31，E为BB 上使BE 1的点。 1 1 1 平面AEC 交DD 于F ，交AD 的延长线于G，求： 1 1 1 1 （Ⅰ）异面直线AD与CG所成角的大小； 1 （Ⅱ）二面角ACGA 的正切值； 1 1 解法一：（Ⅰ）由AD//DG知CGD 为异面直线AD与CG所成角．（如图1） 1 1 1 1 连接C F ．因为ＡＥ和C F 分别是平行平面ABB A和CC DD与平面AECG的交线， 1 1 1 1 1 1 1 所以AE//C F ,由此得DF  BF  3.再由FDG FDA DG  3. 1 1 1  1  在RtC DG中,由CD=1得CGD  1 1 1 1 1 1 6 （Ⅱ）作DH CG于H,由三垂线定理知 1 1 FH CG,故DHF为二面角F-CG-D 1 1 1 1 即二面角ACGA 的平面角. 1 1  3 在RtHDG中,由DG= 3,HGD  得DH  . 1 1 1 6 1 2 DF 3 从而tanDHF  1  2. 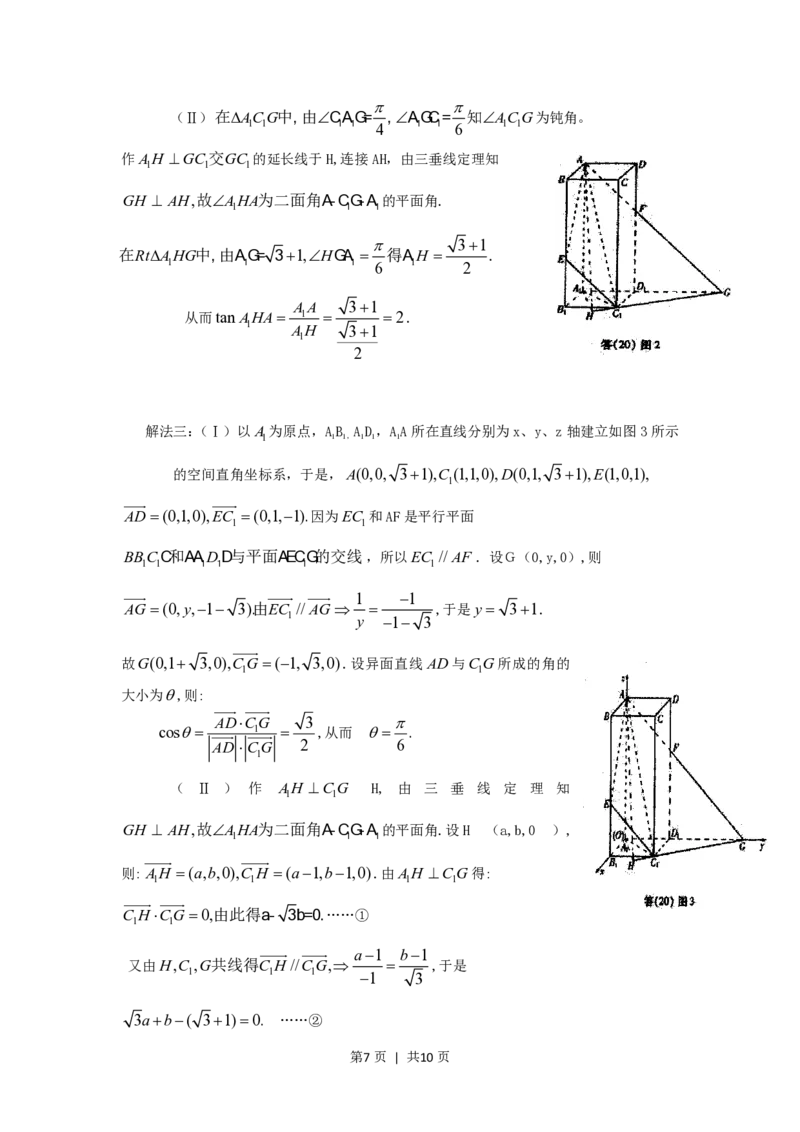1 DH 3 1 2 解法二：（Ⅰ）由AD//DG知CGD 为异面直线AD与CG所成角．（如图2） 1 1 1 1 因为EC 和AF是平行平面BBCC与平面AADD与平面AECG的交线， 1 1 1 1 1 1  所以EC // AF,由此得AGA EC B  , AG  AA  31 DG  3. 1 1 1 1 4 1 1 1  在RtC DG中,由CD=1得CGD  1 1 1 1 1 1 6 第6页 | 共10页  （Ⅱ）在ACG中,由CAG= ,AGC= 知ACG为钝角。 1 1 1 1 4 1 1 6 1 1 作AH GC交GC 的延长线于H,连接AH，由三垂线定理知 1 1 1 GH  AH,故AHA为二面角A-CG-A 的平面角. 1 1 1  31 在RtAHG中,由AG= 31,HGA  得AH  . 1 1 1 6 1 2 AA 31 从而tanAHA 1  2. 1 AH 31 1 2 解法三：（Ⅰ）以A为原点，AB AD，AA所在直线分别为x、y、z轴建立如图3所示 1 1 1， 1 1 1 的空间直角坐标系，于是，A(0,0, 31),C (1,1,0),D(0,1, 31),E(1,0,1), 1   AD(0,1,0),EC (0,1,1).因为EC 和AF是平行平面 1 1 BBCC和AADD与平面AECG的交线，所以EC // AF．设Ｇ（0,y,0）,则 1 1 1 1 1 1    1 1 AG (0,y,1 3).由EC // AG  ,于是y  31. 1 y 1 3  故G(0,1 3,0),CG (1, 3,0).设异面直线 AD与CG所成的角的 1 1 大小为,则:   ADCG 3  cos 1  ,从而  .   AD  CG 2 6 1 （ Ⅱ ） 作 AH CG H, 由 三 垂 线 定 理 知 1 1 GH  AH,故AHA为二面角A-CG-A 的平面角. 设H （a,b,0 ）, 1 1 1   则:AH (a,b,0),C H (a1,b1,0).由AH CG得: 1 1 1 1   C HCG 0,由此得a- 3b=0.……① 1 1   a1 b1 又由H,C ,G共线得C H //CG,  ,于是 1 1 1 1 3 3ab( 31)0. ……② 第7页 | 共10页33 31 33 31 联立①②得:a ,b .故H( , ), 4 4 4 4  3 3 1 3 1 3  由 AH  ( )2 ( )2  , AA 1 3 得: 1 4 4 2 1 AA 31 tanAHA 1  2. 1 AH 31 1 2 （21）（本小题满分12分） 2x b 已知定义域为R的函数 f(x) 是奇函数。 2x1a （Ⅰ）求a,b的值； （Ⅱ）若对任意的tR，不等式 f(t2 2t) f(2t2 k)0恒成立， 求k的取值范围； b1 12x 解：（Ⅰ）因为 f(x)是奇函数，所以 f(x)=0，即 0b1 f(x) a2 a2x1 1 1 12 2 又由f（1）= -f（-1）知  a 2. a4 a1 12x 1 1 （Ⅱ）解法一：由（Ⅰ）知 f(x)   ，易知 f(x)在(,) 22x1 2 2x 1 上 为减函数。又因 f(x)是奇函数，从而不等式： f(t2 2t) f(2t2 k)0 等价于 f(t2 2t)f(2t2 k) f(k2t2)，因 f(x)为减函数，由上式推得： t2 2t k2t2．即对一切tR有：3t2 2tk 0， 1 从而判别式412k 0k  . 3 12x 解法二：由（Ⅰ）知 f(x) ．又由题设条件得： 22x1 12t22t 122t2k  0， 22t22t1 222t2k1 第8页 | 共10页即 ：(22t2k12)(12t22t)(2t22t12)(122t2k)0， 整理得 23t22tk 1,因底数2>1,故: 3t2 2tk 0 1 上式对一切tR均成立，从而判别式412k 0k  . 3 （22）（本小题满分12分） 如图，对每个正整数n，A (x ,y )是抛物线x2 4y上的点， n n n 过焦点F 的直线FA 交抛物线于另一点B (s ,t )。 n n n n （Ⅰ）试证：x s 4(n1)； n n （Ⅱ）取x 2n，并记C 为抛物线上分别以A 与B 为切点的两条切线的交点。 n n n n 试证： FC  FC   FC 2n 2n11； 1 2  n 证明：（Ⅰ）对任意固定的n1,因为焦点F（0,1）,所以可设直线A B 的方程为 n n y1k x,将它与抛物线方程x2 4y联立得: n x2 4k x40, 由 一 元 二 次 方 程 根 与 系 数 的 关 系 得 n x s 4(n1)． n n （Ⅱ）对任意固定的n1,利用导数知识易得抛物线x2 4y在A 处 n x 的切线的斜率k  n ,故x2 4y在A 处的切线的方程为： A n 2 n x y y  n (xx )，……① n 2 n 第9页 | 共10页类似地，可求得x2 4y在B 处的切线的方程为： n s yt  n (xs )，……② n 2 n x s x2 s2 x2 s2 由②－①得：y t  n n x n n  n  n ， n n 2 2 4 4 x s x2 s2 x s n n x n n ,x n n ……③ 2 4 2 x s 将③代入①并注意x s 4得交点C 的坐标为( n n ,1)． n n n 2 x s x2 s2 由两点间的距离公式得： FC 2 ( n n)2 4 n  n 2 n 2 4 4 x2 4 x 2 x 2  n  2( n  )2, FC  n  ． 4 x2 2 x n 2 x n n n 现在x 2n，利用上述已证结论并由等比数列求和公式得： n 1 1 1 1 FC  FC   FC  (x  x   x )2(    ) 1 2  n 2 1 2  n x x  x 1 2 n 1 1 1 1  (222  2n)2(    )(2n 1)(221n)2n 2n11.   2 2 22 2n 第10页 | 共10页