文档内容
高一上数学暑假测试密卷(二)
一、单项选择题:本题共8小题,每小题满分5分,共40分.在每小题给出的四个选项中,只有一项符合
题目要求,选对得5分,选错得0分.
1.设集合 , , ( )
A. B. C. D.
【答案】D
【分析】根据给定条件,利用交集的定义直接求解作答.
【详解】因为集合 , ,
所以 .
故选:D
2.角 的终边过点 ,则 ( )
A. B. C. D.
【答案】A
【分析】根据任意角的三角函数的定义计算可得.
【详解】已知角 的终边经过点 ,所以 .
故选:A
3.已知 ,且 则 的值为
A.4 B.0 C. D.
【答案】A
【详解】设 ,
本题选择A选项.4.设 , , ,则a,b,c的大小关系是( )
A. B.
C. D.
【答案】B
【分析】根据指、对数函数的知识判断出 的范围即可.
【详解】因为 , ,
所以
故选:B
5.已知函数 ,则 的零点所在的区间为( )
A. B. C. D.
【答案】D
【分析】根据零点存在定理,只需判断两个端点的函数值,即两个端点函数值异号即可.
【详解】由已知得 , , , ,
,
所以 ,由零点的存在定理得, 的零点所在的区间为 ,
故选:D.
6.酒驾是严重危害交通安全的违法行为.根据国家有关规定:驾驶人血液中的酒精含量大于(或等于)
毫克/毫升,小于 毫克/毫升的情况下驾驶机动车属于饮酒驾车;含量大于(或等于) 毫克/毫升
的情况下驾驶机动车属于醉酒驾车.假设某驾驶员一天晚上 点钟喝了一定量的酒后,其血液中酒精含量
上升到 毫克/毫升.如果在停止喝酒后,他血液中酒精含量以每小时 的速度减少,则他次日上午最早
( )点(结果取整数)开车才不构成酒驾.(参考数据: , )
A. B. C. D.
【答案】D
【分析】根据题意可得不等式 ,解不等式可求得 ,由此可得结论.【详解】假设经过 小时后,驾驶员开车才不构成酒驾,
则 ,即 , ,
则 , ,
次日上午最早 点,该驾驶员开车才不构成酒驾.
故选:D.
7.已知 , ,则 的值为( )
A. B. C. D.
【答案】C
【分析】将条件中两式平方相加后整理即可得答案.
【详解】 ,
,
两式相加得 ,
.
故选:C.
8.已知函数 ,若方程 有四个不同的根 ,则 的取值范围为
( )
A. B.
C. D.
【答案】B【分析】分析给定的函数性质,画出函数 的部分图象,确定a的取值范围,进而求出 范围
作答.
【详解】函数 ,当 时, 单调递增, ,
当 时, 单调递减, ,
当 时, 在 上递减,在 上递增, ,
作出函数 的部分图象,如图,
方程 有四个不同的根 ,不妨令 ,即直线 与函数 的图象有4
个公共点,
观察图象知, , ,
显然有 ,且 ,由 得 ,
即 ,则有 ,因此 ,
所以 的取值范围为 .
故选:B
【点睛】关键点睛:涉及用分段函数零点特性求参数范围问题,可以先独立分析各段上的零点,再综合考
查所有零点是解决问题的关键.二、多项选择题:本题共4小题,每小题满分5分,共20分. 在每小题给出的四个选项中,有多项符合
题目要求。全部选对得5分,部分选对得2分,有选错的得0分.
9.已知函数 ,则( )
A. 的定义域为
B. 的单调递减区间为
C. 是增函数
D. 的值域为
【答案】ACD
【分析】对于A,由 且 ,求解即可判断;对于B,区间 不在定义域内,即可判断;
对于C,根据复合函数的单调性判断方法即可判断;对于D,可得真数能取遍所有大于0的数,从而可判
断.
【详解】对于A,由 且 ,得 ,故 的定义域为 ,A对;
对于B,区间 不在定义域内,B错;
对于C, 函数 在 为增函数,
函数 在 为增函数
故函数 的单调递增区间为 ,无单调递减区间,C对;
对于D, 在 为增函数,
真数能取遍所有大于0的数,故值域为R,D对.
故选:ACD.
10.下列运算中,结果是1的是( )
A. B. C. D.【答案】BCD
【分析】根据特殊角的三角函数值,结合正切的两角差公式、二倍角的正弦公式、诱导公式逐一计算判断
即可.
【详解】A:因为 ,所以不符合题意;
B:因为 ,所以符合题意;
C:因为 ,所以符合题意;
D: ,符合题意,
故选:BCD
11.下列结论正确的是( ).
A.若 ,则 的最大值为
B.若 , ,则
C.若 , ,且 ,则 的最大值为9
D.若 ,则 的最大值为2
【答案】ABD
【解析】利用基本不等式,逐项判断,即可得出结果.
【详解】A选项,由 可得 ,当且仅当 ,即
时,等号成立;即 的最大值为 ;A正确;
B选项,由 , ,可得 ,即 ,故B正确;
C选项,若 , ,且 ,则 ,
当且仅当 ,即 时,等号成立;即 的最小值为9,故C错;
D选项,因为 ,所以 ,当且仅当 ,即 时,等号成立,
故D正确.
故选:ABD.
【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把
构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不
是所求的最值,这也是最容易发生错误的地方.
12.设函数 的定义域为 ,若存在常数 ,使 对一切实数 均成立,则称 为
“倍约束函数”.现给出下列函数是“倍约束函数”的有( )
A.
B. ;
C. ;
D. 是定义在实数集 上的奇函数,且对一切 , 均有
【答案】AD
【分析】结合新定义,逐项证明或举出反例即可得解.
【详解】对于A,函数 ,存在实数 ,使得 恒成立,故A正确;
对于B,函数 ,若要使 恒成立,则当 时, 恒成立,不存在这样的实数 ,故B错误;
对于C, ,
由 恒成立,可得 不是“倍约束函数”,故C错误;
对于D,由函数 是定义在R上的奇函数,得 ,
当 时,可得 成立,所以该函数是“倍约束函数”,故D正确.
故选:AD.
三、填空题:本题共4小题,每小题5分,共20分。
13.计算 .
【答案】
【分析】直接利用对数的运算性质及指数幂的运算可得答案.
【详解】 .
故答案为: .
14.已知 , ,则 .
【答案】
【分析】根据诱导公式结合条件即得.
【详解】因为 ,
所以 .
故答案为: .
15.《乐府诗集》辑有晋诗一组,属清商曲辞吴声歌曲,标题为《子夜四时歌七十五首》.其中《夏歌二十首》的第五首曰:叠扇放床上,企想远风来.轻袖佛华妆,窈窕登高台、诗里的叠扇,就是折扇.折扇展开后
可看作是半径为 的扇形,是圆面的一部分,如图所示.设某扇形的面积为 ,该扇形所在圆面的面积为 ,
当 与 的比值为 时,该扇面为“黄金美观扇面”.若某扇面为“黄金美观扇面”,扇形的半径
,则此时的扇形面积为 .
【答案】
【分析】利用 与 比值,列出方程即可.
【详解】 ,
扇形所在圆面的面积为:
且:
;
故答案为:
16.若存在实数 ,使得函数 在区间 上单调递减,且 在区间上的取值范围为 ,则 的取值范围为 .
【答案】
【分析】根据 ,去绝对值符号化简 ,根据对勾函数的性质,判断 的单调性,根据题意
建立 之间的等式关系,将 消掉后化简可得 ,代入到方程组中可建立 与 和 与 的等
式关系,通过移项变形,将两式形式化为统一,构造函数画出图象,列出不等式解出即可.
【详解】解:因为 ,
因为 ,所以 , ,所以 ,
取 ,根据对勾函数性质可知:
在 上, 单调递减,在 上, 单调递增,
所以 在 上, 单调递增,在 上, 单调递减,
因为 区间 上单调递减,所以 ,
因为 区间 上单调递减,所以 ,
即 ,即 ,
即 ,化简可得 ,
因为 ,所以 ,代入 中,
化简可得: ,当 时方程组不成立,所以方程组可化为 ,
即 在 上与 有两个不同交点,
因为 ,当 时, ,
当 时, ,当 时, ,
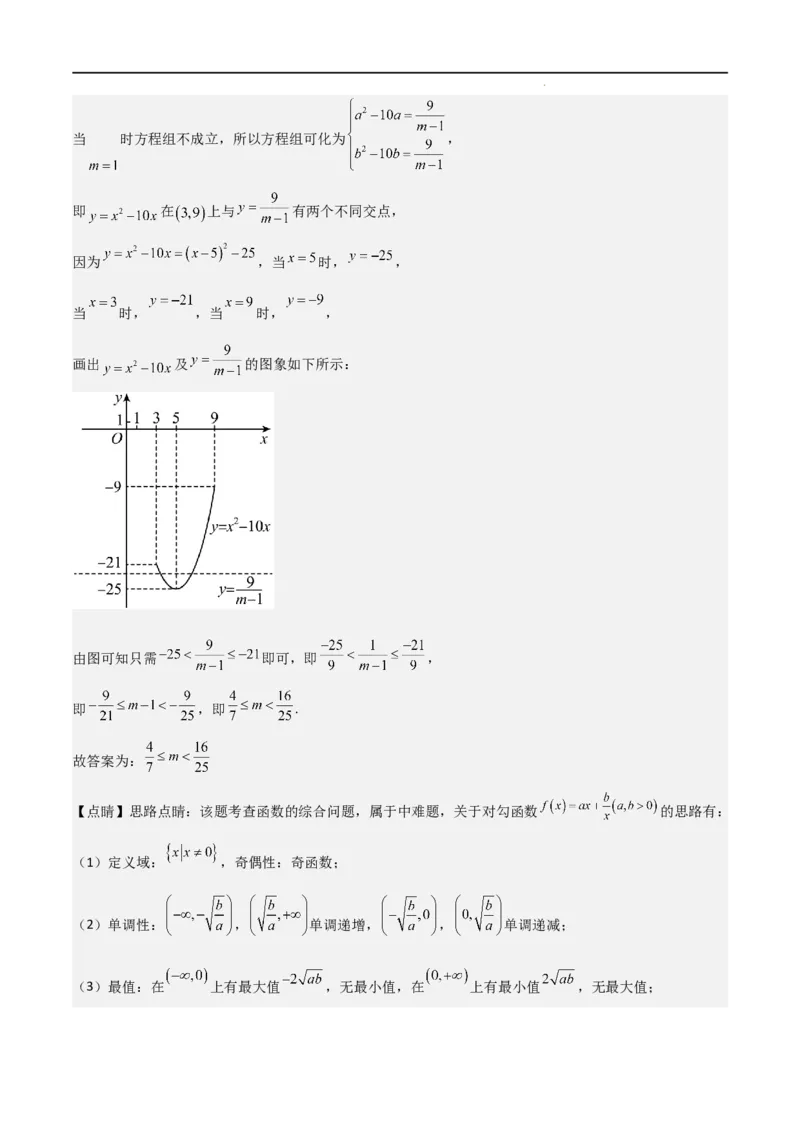
画出 及 的图象如下所示:
由图可知只需 即可,即 ,
即 ,即 .
故答案为:
【点睛】思路点睛:该题考查函数的综合问题,属于中难题,关于对勾函数 的思路有:
(1)定义域: ,奇偶性:奇函数;
(2)单调性: , 单调递增, , 单调递减;
(3)最值:在 上有最大值 ,无最小值,在 上有最小值 ,无最大值;(4)渐近线: 轴和 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知角α的始边与x轴的非负半轴重合,终边过点 .
(1)求 的值;
(2)求 的值.
【答案】(1) ;
(2) .
【分析】(1)根据给定条件,利用三角函数定义计算作答.
(2)利用诱导公式化简,结合(1)的结论,用齐次式法计算作答.
【详解】(1)角 的始边与x轴的非负半轴重合,终边过点 ,
所以 .
(2)由(1)知, ,
所以 .
18.已知函数 .
(1)若 ,求 的最小值;
(2)若 ,求关于 的不等式 的解集.
【答案】(1)
(2)【分析】(1)利用代入法,结合基本不等式进行求解即可;
(2)利用代入法,结合一元二次不等式的解法进行求解即可.
【详解】(1)由 可得: ,
因为 ,所以 ,
所以 ,
当且仅当 时取等号,即当且仅当 时取得最小值为 ;
(2)由 可得: ,
则 化为:
因为 ,所以 ,
则解不等式可得 或 ,
则不等式的解集为 .
19.已知函数 为定义在 上的奇函数.
(1)若当 时, ,求 在 上的解析式;
(2)若 在 上单调递增, ,且 ,求实数m的取值范围..
【答案】(1)(2)
【分析】(1)利用奇函数的定义,定义域关于原点对称以及 ,可以求出函数表达式;
(2)利用偶函数的性质及函数的单调性,得到 在定义区间上是增函数,自变量越大,函数值也越大,
得到不等式组,然后求解.
【详解】(1)当 时, ,
当 时, ,
则 ,
∴ ,
∴
(2)∵ 为奇函数,∴ ,
,
∴ 为偶函数,且 在 上为增函数, ,
∴ ∴ ∴ ,
∴m的取值范围为 .
20.为宣传2022年北京冬奥会,某公益广告公司拟在一张矩形海报纸(记为矩形 ,如图)上设计
三个等高的宣传栏(栏面分别为一个等腰三角形和两个全等的直角梯形),宣传栏(图中阴影部分)的面积之和为 .为了美观,要求海报上所有水平方向和竖直方向的留空宽度均为 .设直角梯形的高为
.
(1)当 时,求海报纸的面积;
(2)为节约成本,应如何选择海报纸的尺寸,可使用纸量最少(即矩形 的面积最小)?
【答案】(1)
(2)当海报纸宽为 ,长为 ,可使用纸量最少.
【分析】(1)根据已知条件,先求出梯形长的底边 ,再分别求出 , ,即可
求解;
(2)根据已知条件,结合基本不等式的公式,即可求解.
【详解】(1) 宣传栏(图中阴影部分)的面积之和为 ,直角梯形的高为 ,
则梯形长的底边 ,
海报上所有水平方向和竖直方向的留空宽度均为 ,
, ,
故海报面积为 .
(2) 直角梯形的高为 ,宣传栏(图中阴影部分)的面积之和为 ,
,海报上所有水平方向和竖直方向的留空宽度均为 ,
海报宽 ,海报长 ,
故 ,
当且仅当 ,即 ,
故当海报纸宽为 ,长为 ,可使用纸量最少.
21.已知函数 , .
(1)若 在区间 上是单调函数,则 的取值范围;
(2)在(1)的条件下,是否存在实数 ,使得函数 与函数 的图象在区间 上有唯一的交点,若
存在,求出 的范围,若不存在,请说明理由.
【答案】(1) 或 ;
(2)存在,且 的取值范围是 .
【分析】(1)分 、 两种情况讨论,根据函数 在区间 上单调可出关于 的不等式,综
合可得出实数 的取值范围;
(2)分 、 、 、 四种情况讨论,分析两个函数在区间 上的单调性,根据已知条
件可得出关于实数 的不等式(组),综合可解得实数 的取值范围.
【详解】(1)解:当 时 在 上单调递减.
当 时, 是二次函数,其对称轴为直线 ,
在区间 上是单调函数, 或 ,即 或 ,
解得: 或 或 .
综上: 或 .(2)解:①当 时, 单调递减, 单调递增,
则函数 单调递增,
因为 , ,
由零点存在定理可知,存在唯一的 使得 ,
此时,函数 与函数 在区间 上的图象有唯一的交点,合乎题意;
②当 时,二次函数 的图象开口向下,对称轴为直线 ,
所以, 在 上单调递减, 单调递增,
则函数 在 上单调递增,
要使得函数 与函数 的图象在区间 上有唯一的交点,
则 ,解得 ,此时 ;
③当 时,二次函数 的图象开口向上,对称轴 ,
则 在 上单调递减, 在 上单调递增,
则函数 在 上单调递增,
要使得函数 与函数 的图象在区间 上有唯一的交点,
则 ,解得 ,此时 ;
④当 时,二次函数 的图象开口向上,对称轴 ,
所以, 在 上单调递增, 在 上单调递增,则 , ,所以, 在 上恒成立,
此时,函数 与函数 的图象在区间 上没有交点.
综上所述,实数 的取值范围是 .
【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,
利用数形结合的方法求解.
22.已知函数 满足 ,当 时, 成立,且 .
(1)求 ,并证明函数 的奇偶性;
(2)当 ,不等式 恒成立,求实数 的取值范围.
【答案】(1) ,证明见解析;
(2) .
【分析】(1)令 ,可得 ,令 , ,从而即可证明;
(2)由已知条件,可得 为增函数,又原不等式等价于 恒成立,则
在 上恒成立,令 ,分离参数 即可求解.
【详解】(1)解:令 ,可得 ,
令 ,则 ,所以 ,
所以 ,所以 为奇函数;
(2)解: ,即 ,
所以 ,
又当 时, 成立,所以 为增函数,
所以 在 上恒成立,
令 ,可得 在 上恒成立,
又 , ,所以当 时, ,
所以 ,即 .