文档内容
专题03 空间向量的应用
一、单选题
1.(2020·贵州省铜仁第一中学高二开学考试)已知两个异面直线的方向向量分别为 , ,且| |=| |
=1, • ,则两直线的夹角为( )
A. B.
C. D.
【答案】B
【解析】
设两直线的夹角为θ,则由题意可得1×1×cos , ,∴cos , ,
∴ , ,∴θ ,
故选: .
2.(2019·穆棱市第一中学高二期末)若平面 的法向量分别为 ,则(
)
A. B. 与 相交但不垂直
C. D. 或 与 重合
【答案】D
【解析】
因为 ,所以平面 的法向量共线,故 或 与 重合.
故选:D.3.(2020·北京高二期末)已知直线 的方向向量为 ,平面 的法向量为 ,则“ ”是“ ∥ ”
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B
【解析】
,即 ,不一定有 ∥ ,也可能
“ ”是“ ∥ ”的不充分条件
∥ ,可以推出 ,
“ ”是“ ∥ ”是必要条件,
综上所述, “ ”是“ ∥ ”必要不充分条件.
故选:B.
4.(2019·山东省济南一中高二期中)在平面ABCD中, , , ,若
,且 为平面ABCD的法向量,则 等于( )
A.2 B.0 C.1 D.无意义
【答案】C
【解析】
由题得, , ,又 为平面ABCD的法向量,则有 ,即,则 ,那么 .
故选:C
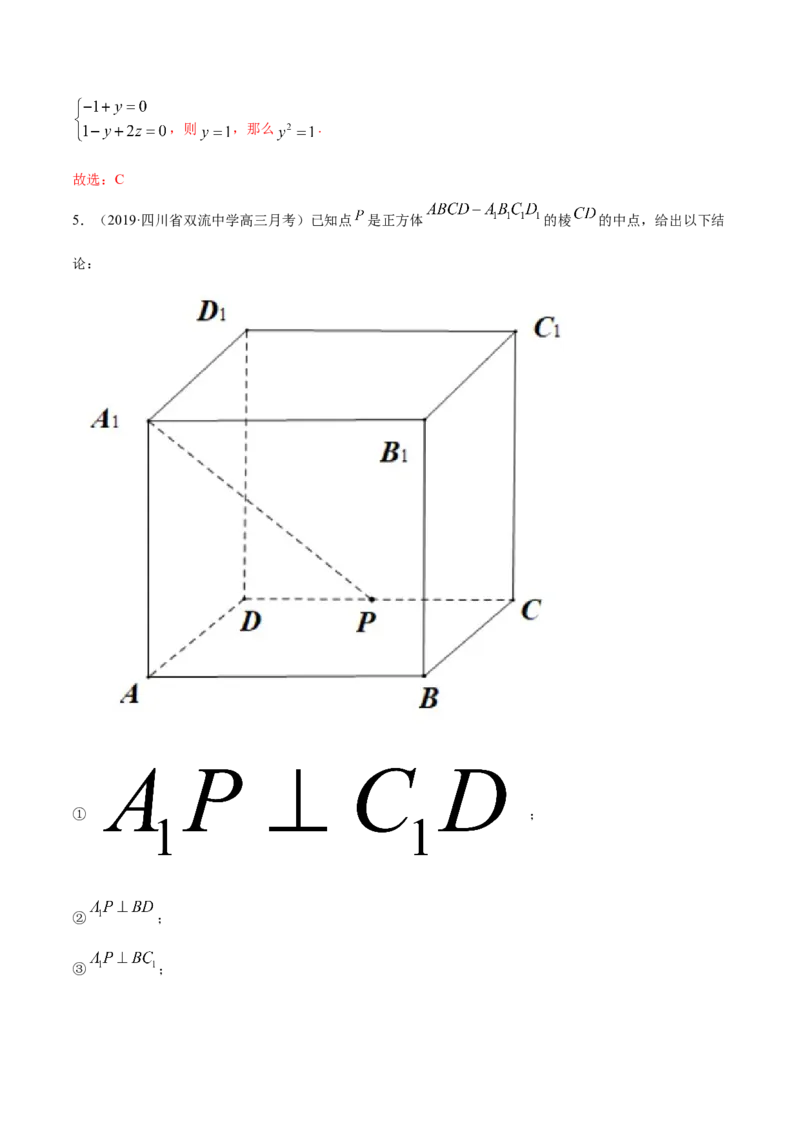
5.(2019·四川省双流中学高三月考)已知点 是正方体 的棱 的中点,给出以下结
论:
① ;
② ;
③ ;④ 平面
其中正确命题的序号是( )
A.① B.② C.③ D.④
【答案】C
【解析】
设正方体边长为2,建立如图空间直角坐标系.则 .
对①, ,因为 ,故①错误.
对②, ,因为 ,故②错误.
对③, ,因为 ,故③正确.
对④,由②有 不成立,故 平面 不成立.故④错误.
故选:C
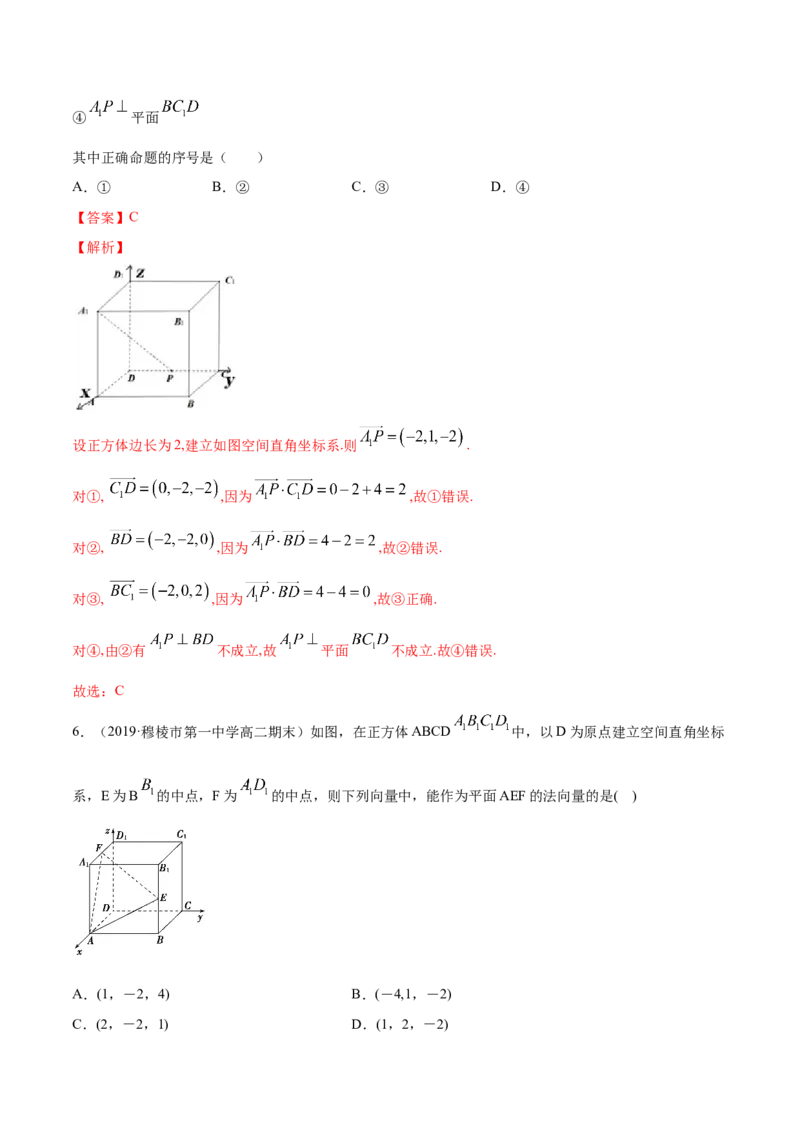
6.(2019·穆棱市第一中学高二期末)如图,在正方体ABCD 中,以D为原点建立空间直角坐标
系,E为B 的中点,F为 的中点,则下列向量中,能作为平面AEF的法向量的是( )
A.(1,-2,4) B.(-4,1,-2)
C.(2,-2,1) D.(1,2,-2)【答案】B
【解析】
设正方体棱长为2,则A(2,0,0),E(2,2,1),F(1,0,2),
∴ =(0,2,1), =(﹣1,0,2)
设向量 =(x,y,z)是平面AEF的一个法向量
则 ,取y=1,得x=﹣4,z=﹣2
∴ =(﹣4,1,﹣2)是平面AEF的一个法向量
因此可得:只有B选项的向量是平面AEF的法向量
故选:B.
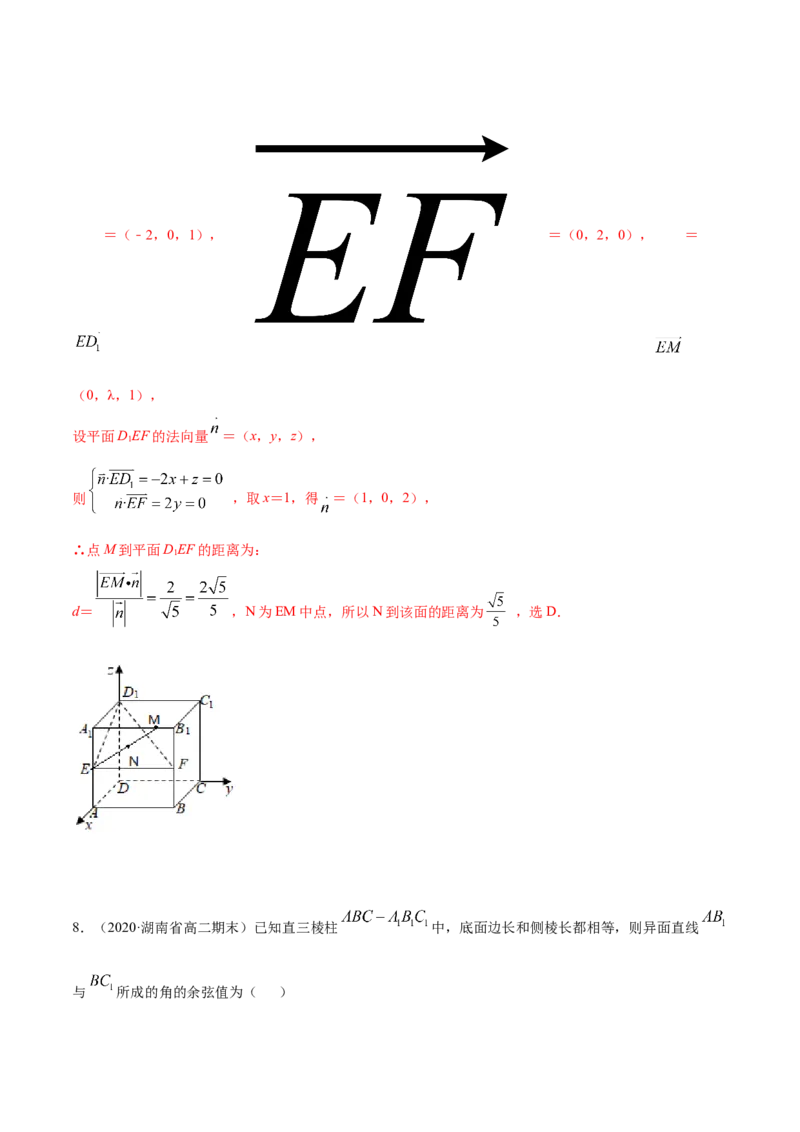
7.(2019·包头市第四中学高二期中)在棱长为2的正方体 中, , 分别为棱 、
的中点, 为棱 上的一点,且 ,设点 为 的中点,则点 到平面
的距离为( )
A. B. C. D.
【答案】D
【解析】
以D为原点,DA为x轴,DC为y轴,DD 为z轴,建立空间直角坐标系,
1
则M(2,λ,2),D(0,0,2),E(2,0,1),F(2,2,1),
1=(﹣2,0,1), =(0,2,0), =
(0,λ,1),
设平面DEF的法向量 =(x,y,z),
1
则 ,取x=1,得 =(1,0,2),
∴点M到平面DEF的距离为:
1
d= ,N为EM中点,所以N到该面的距离为 ,选D.
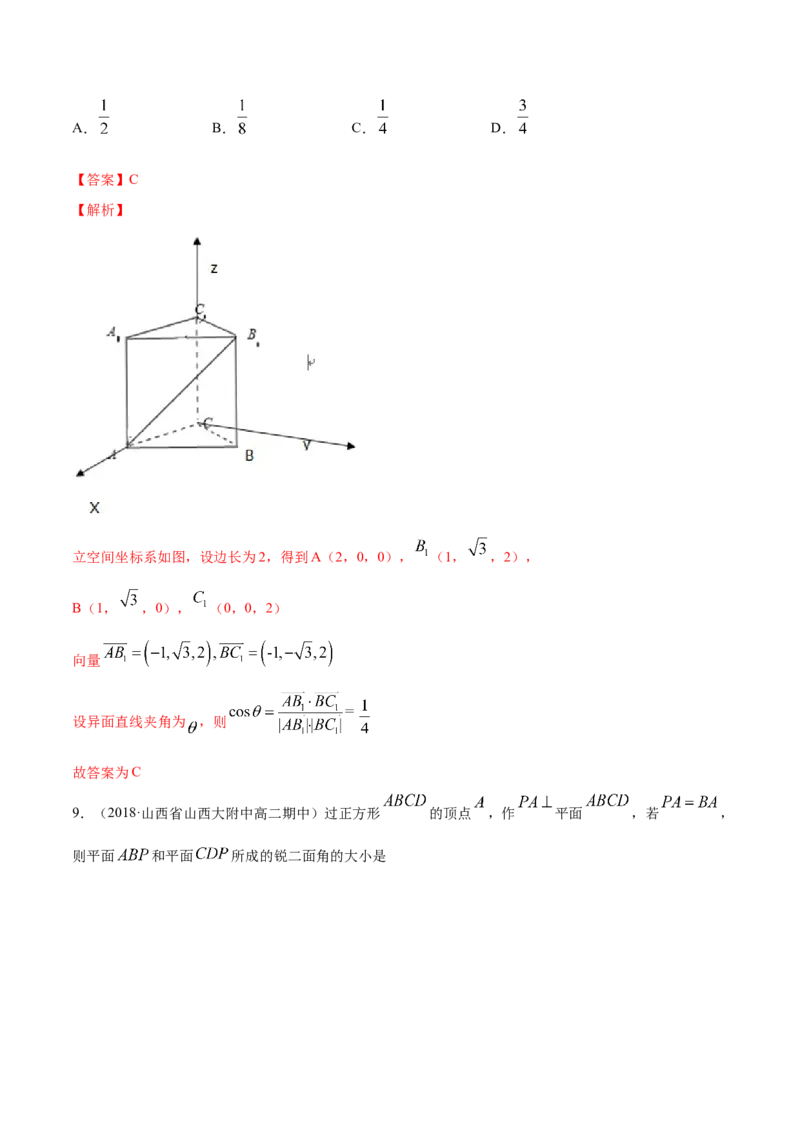
8.(2020·湖南省高二期末)已知直三棱柱 中,底面边长和侧棱长都相等,则异面直线
与 所成的角的余弦值为( )A. B. C. D.
【答案】C
【解析】
立空间坐标系如图,设边长为2,得到A(2,0,0), (1, ,2),
B(1, ,0), (0,0,2)
向量
设异面直线夹角为 ,则
故答案为C
9.(2018·山西省山西大附中高二期中)过正方形 的顶点 ,作 平面 ,若 ,
则平面 和平面 所成的锐二面角的大小是A. B.
C. D.
【答案】B
【解析】
法一:建立如图(1)所示的空间直角坐标系,不难求出平面APB与平面PCD的法向量分别为n=(0,1,0),n
1 2
=(0,1,1),故平面ABP与平面CDP所成二面角的余弦值为 = ,故所求的二面角的大小是45°.
法二:将其补成正方体.如图(2),不难发现平面ABP和平面CDP所成的二面角就是平面ABQP和平面
CDPQ所成的二面角,其大小为45°.
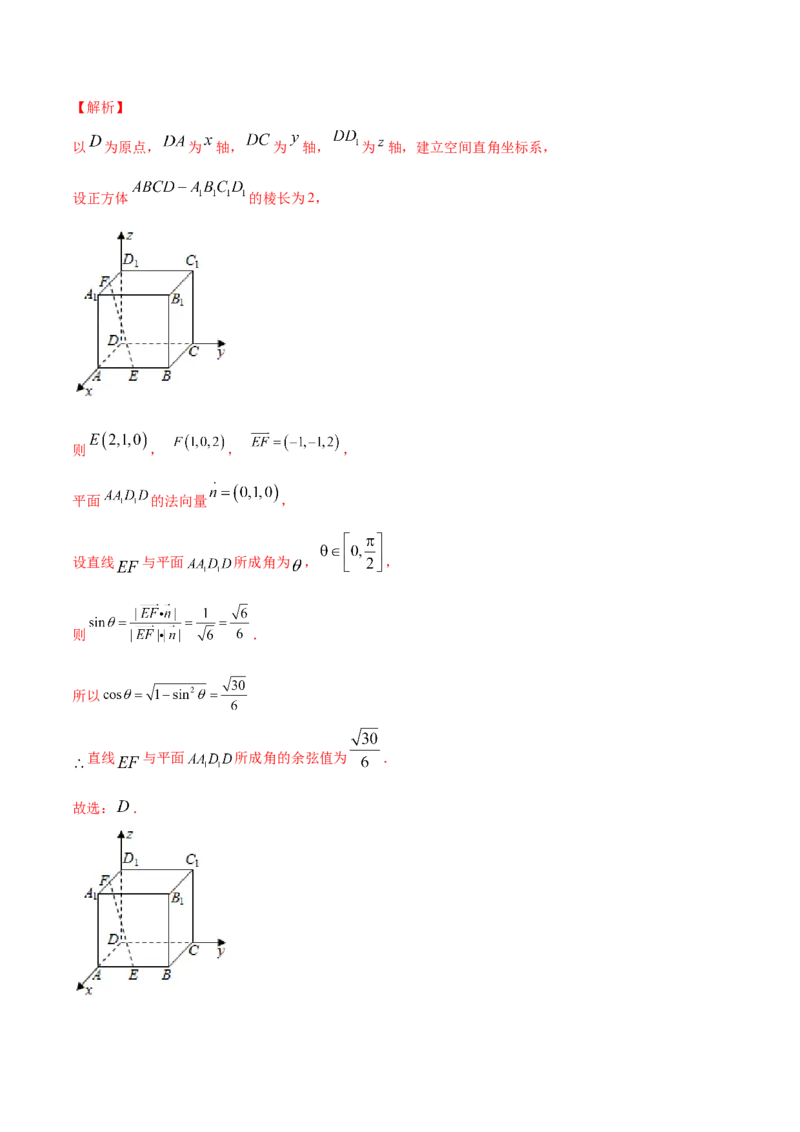
10.(2020·山东省章丘四中高二月考)在正方形 中,棱 , 的中点分别为 ,
,则直线EF与平面 所成角的余弦值为( )
A. B. C. D.
【答案】D【解析】
以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,
设正方体 的棱长为2,
则 , , ,
平面 的法向量 ,
设直线 与平面 所成角为 , ,
则 .
所以
直线 与平面 所成角的余弦值为 .
故选: .二、多选题
11.(2020·山东省高二期末)已知ν为直线l的方向向量, , 分别为平面α,β的法向量(α,β不重
合),那么下列选项中,正确的是( )
A. B.
C. D.
【答案】AB
【解析】
A选项,平面α,β不重合,所以平面α,β的法向量平行等价于平面α,β平行,正确;
B选项,平面α,β不重合,所以平面α,β的法向量垂直等价于平面α,β垂直,正确;
C选项,直线的方向向量平行于平面的法向量等价于直线垂直于平面,错误;
D选项,直线的方向向量垂直于平面的法向量等价于直线平行于平面或直线在平面内,错误.
故选:AB
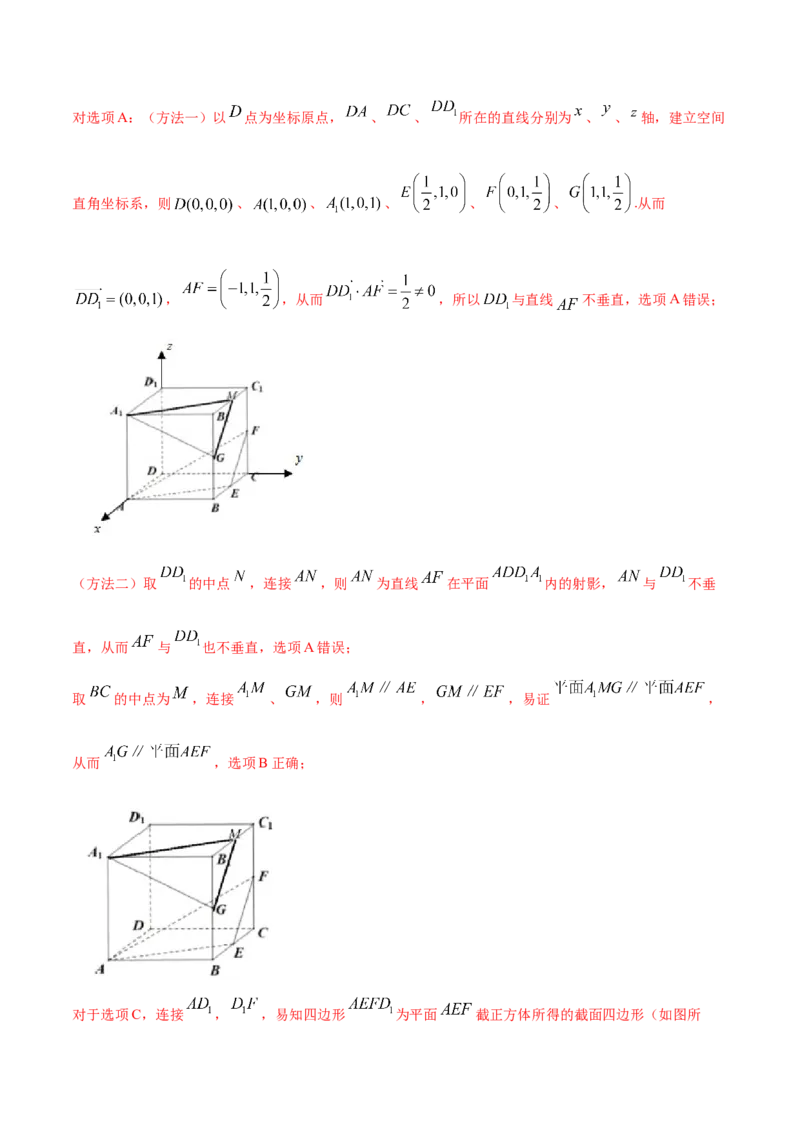
12.(2019·山东省高三)正方体 的棱长为1, 分别为 的中点.则
( )
A.直线 与直线 垂直 B.直线 与平面 平行
C.平面 截正方体所得的截面面积为 D.点 和点 到平面 的距离相等
【答案】BC
【解析】对选项A:(方法一)以 点为坐标原点, 、 、 所在的直线分别为 、 、 轴,建立空间
直角坐标系,则 、 、 、 、 、 .从而
, ,从而 ,所以 与直线 不垂直,选项A错误;
(方法二)取 的中点 ,连接 ,则 为直线 在平面 内的射影, 与 不垂
直,从而 与 也不垂直,选项A错误;
取 的中点为 ,连接 、 ,则 , ,易证 ,
从而 ,选项B正确;
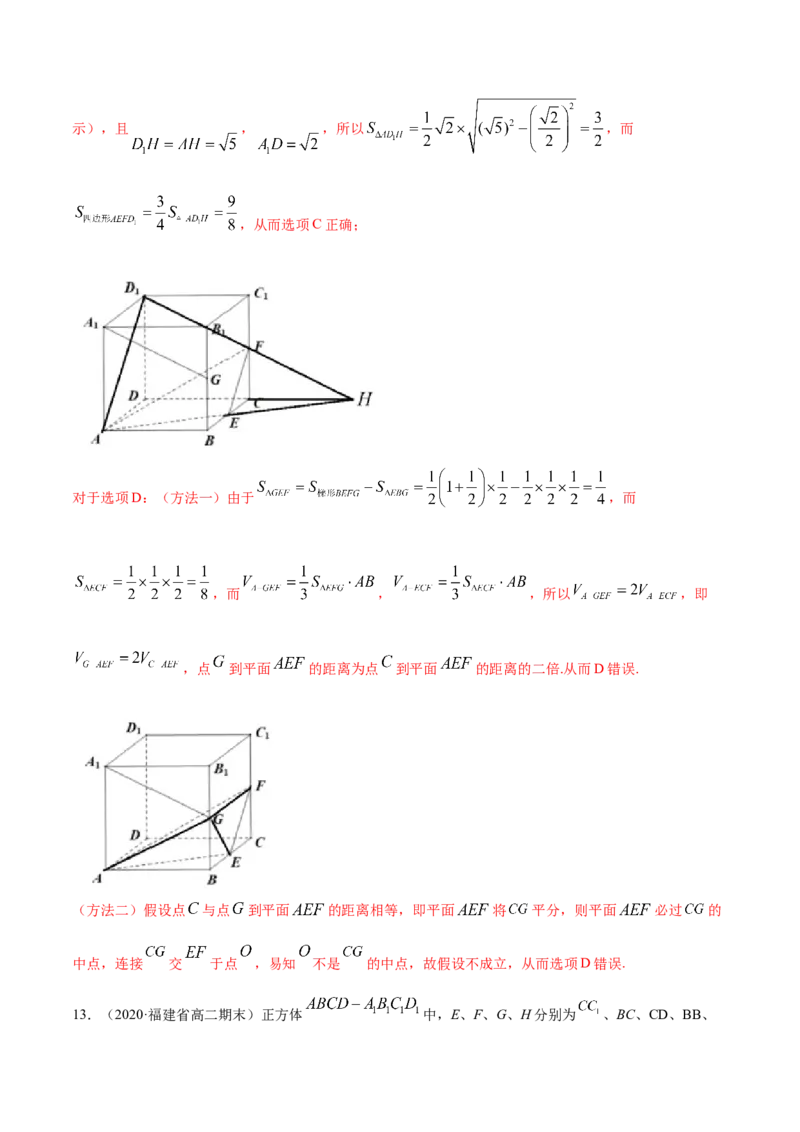
对于选项C,连接 , ,易知四边形 为平面 截正方体所得的截面四边形(如图所示),且 , ,所以 ,而
,从而选项C正确;
对于选项D:(方法一)由于 ,而
,而 , ,所以 ,即
,点 到平面 的距离为点 到平面 的距离的二倍.从而D错误.
(方法二)假设点 与点 到平面 的距离相等,即平面 将 平分,则平面 必过 的
中点,连接 交 于点 ,易知 不是 的中点,故假设不成立,从而选项D错误.
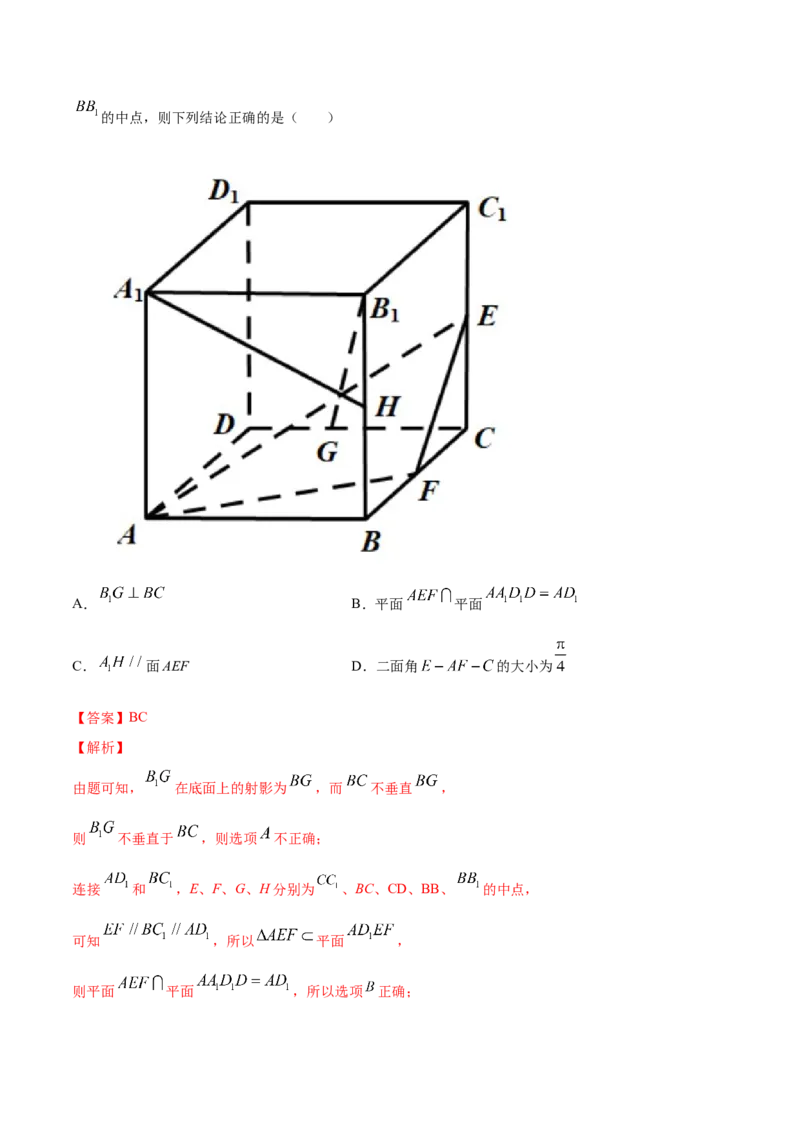
13.(2020·福建省高二期末)正方体 中,E、F、G、H分别为 、BC、CD、BB、的中点,则下列结论正确的是( )
A. B.平面 平面
C. 面AEF D.二面角 的大小为
【答案】BC
【解析】
由题可知, 在底面上的射影为 ,而 不垂直 ,
则 不垂直于 ,则选项 不正确;
连接 和 ,E、F、G、H分别为 、BC、CD、BB、 的中点,
可知 ,所以 平面 ,
则平面 平面 ,所以选项 正确;由题知,可设正方体的棱长为2,
以 为原点, 为 轴, 为 轴, 为 轴,
则各点坐标如下:
,
设平面 的法向量为 ,
则 ,即 ,令 ,得 ,
得平面 的法向量为 ,
所以 ,所以 平面 ,则 选项正确;
由图可知, 平面 ,所以 是平面 的法向量,
则 .
得知二面角 的大小不是 ,所以 不正确.
故选:BC.三、填空题
14.(2019·山东省济南一中高二期中)若平面 的一个法向量为 ,直线l的一个方向向量
为 ,则l与 所成角的正弦值为________.
【答案】
【解析】
由题,设l与 所成角为 ,可得 .
故答案为:
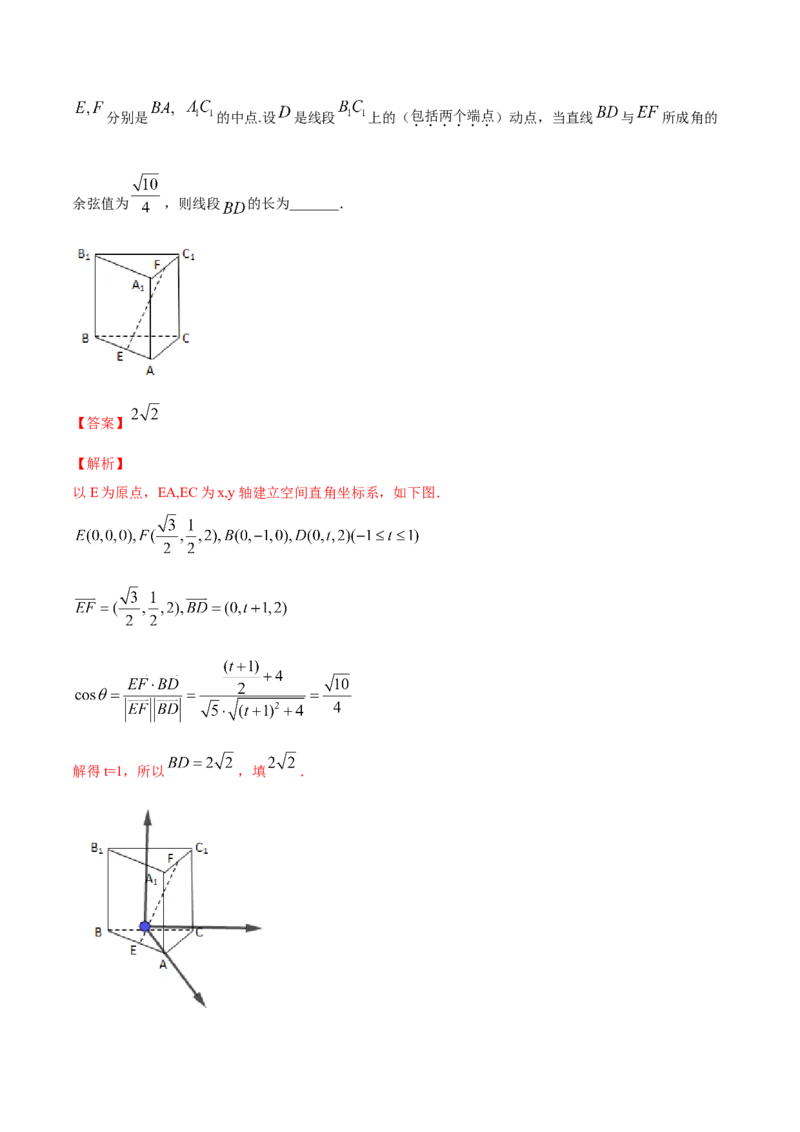
15.(2019·陕西省西北大学附中高二期中)如图,在正三棱柱 中,分别是 的中点.设 是线段 上的(包括两个端点)动点,当直线 与 所成角的
余弦值为 ,则线段 的长为_______.
【答案】
【解析】
以E为原点,EA,EC为x,y轴建立空间直角坐标系,如下图.
解得t=1,所以 ,填 .点睛:利用空间向量求解空间角与距离的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角
坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;
第四,破“应用公式关”.
16.(2019·浙江省宁波市鄞州中学高二期中)正方体 中, 分别是 的中点,
则 与直线 所成角的大小为______ ; 与对角面 所成角的正弦值是 __________.
【答案】
【解析】
如图所示建立空间直角坐标系,设正方体的边长为 ,
则 , , , ,故 , .
故 ,故 与直线 所成角的大小为 .
易知对角面 的一个法向量为 ,设 与对角面 所成角为 ,
故 .
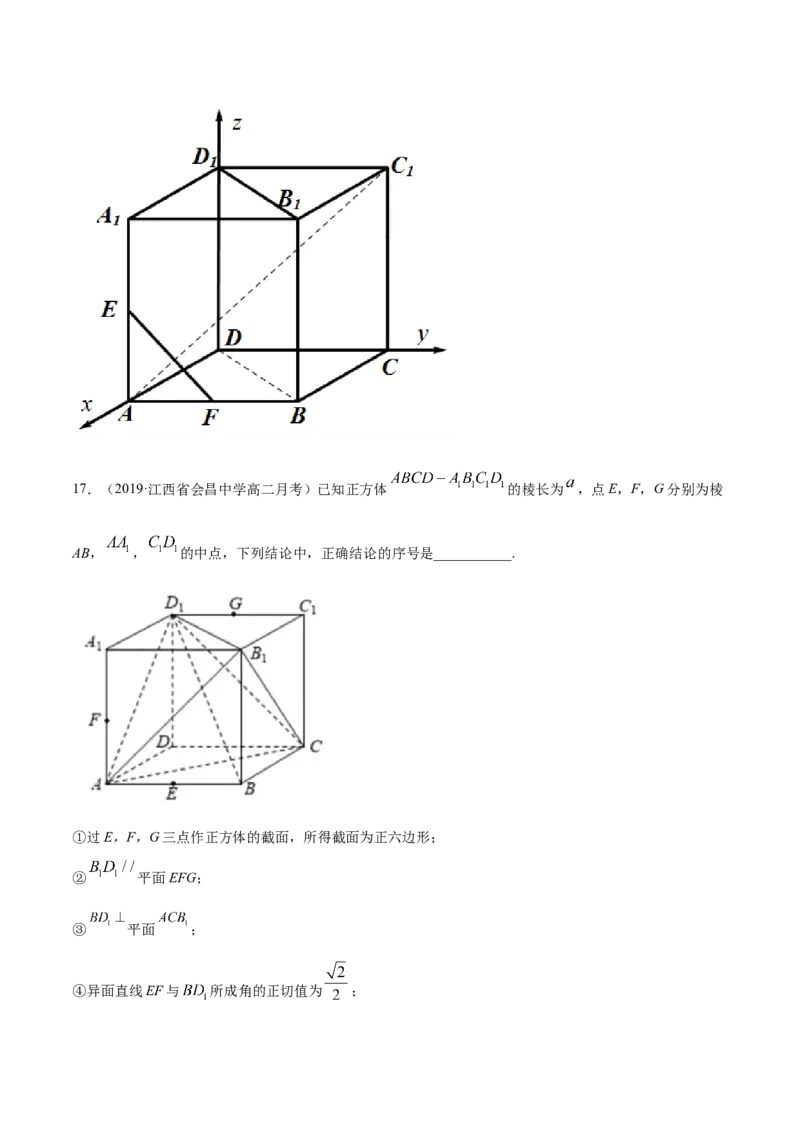
故答案为: ; .17.(2019·江西省会昌中学高二月考)已知正方体 的棱长为 ,点E,F,G分别为棱
AB, , 的中点,下列结论中,正确结论的序号是___________.
①过E,F,G三点作正方体的截面,所得截面为正六边形;
② 平面EFG;
③ 平面 ;
④异面直线EF与 所成角的正切值为 ;⑤四面体 的体积等于 .
【答案】①③④
【解析】
延长EF分别与 , 的延长线交于N,Q,连接GN交 于H,设HG与 的延长线交于P,
连接PQ交 于 ,交BC于M,连FH,HG,GI,IM,ME, ,
如图:则截面六边形EFHGIM为正六边形,故①正确:
因为 与HG相交,故 与平面EFG相交,所以②不正确:
(三垂线定理),
(三垂线定理),
且AC与 相交,
所以 平面 ,故③正确;
以 为原点, 分别为 轴建立空间直角坐标系,
则 ,
则 , ,
所以 ,
所以 ,
所以 ,
所以异面直线EF与 的夹角的正切值为 ,故④正确;
因为四面体 的体积等于正方体的体积减去四个正三棱锥的体积,即为 ,故⑤不正确.
故答案为:①③④
四、解答题
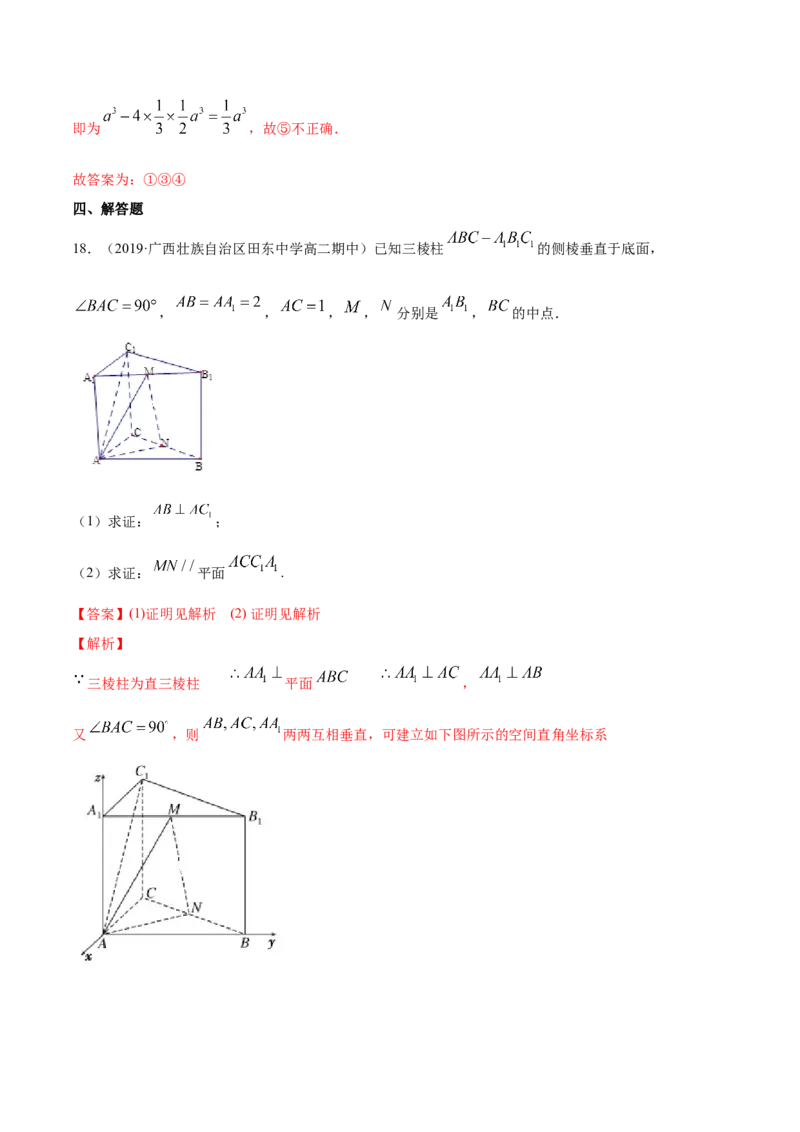
18.(2019·广西壮族自治区田东中学高二期中)已知三棱柱 的侧棱垂直于底面,
, , , , 分别是 , 的中点.
(1)求证: ;
(2)求证: 平面 .
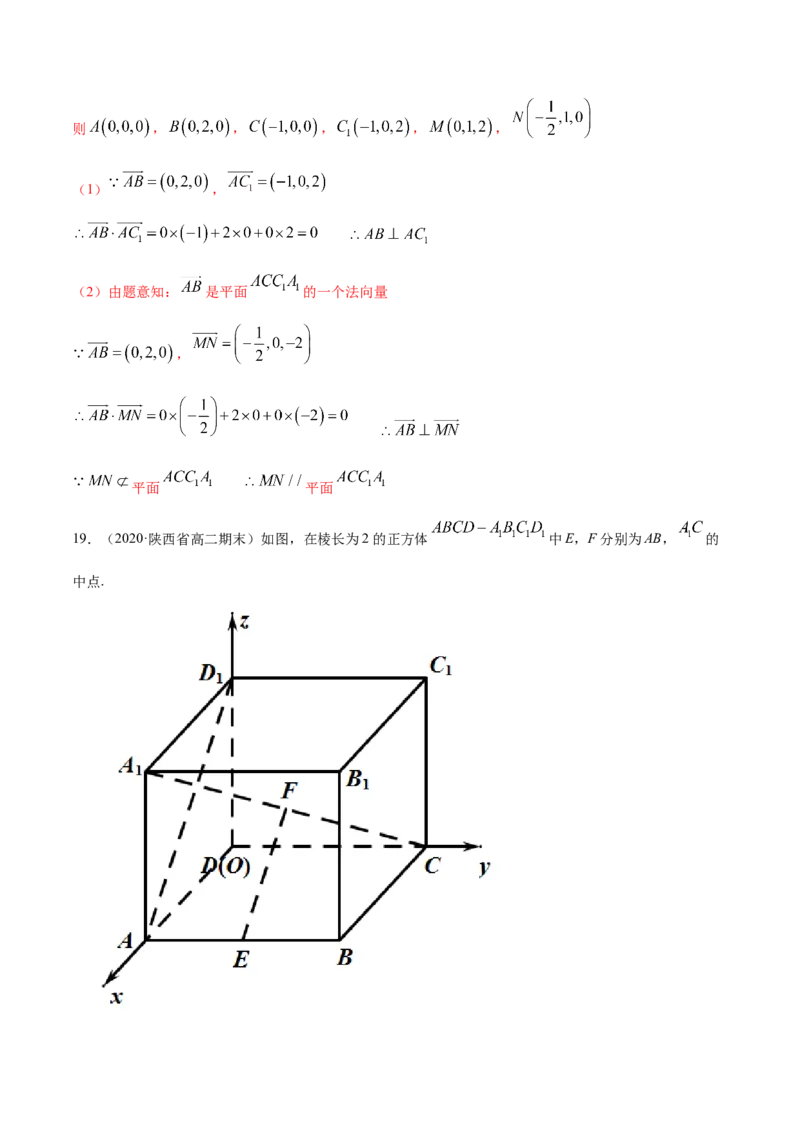
【答案】(1)证明见解析 (2) 证明见解析
【解析】
三棱柱为直三棱柱 平面 ,
又 ,则 两两互相垂直,可建立如下图所示的空间直角坐标系则 , , , , ,
(1) ,
(2)由题意知: 是平面 的一个法向量
,
平面 平面
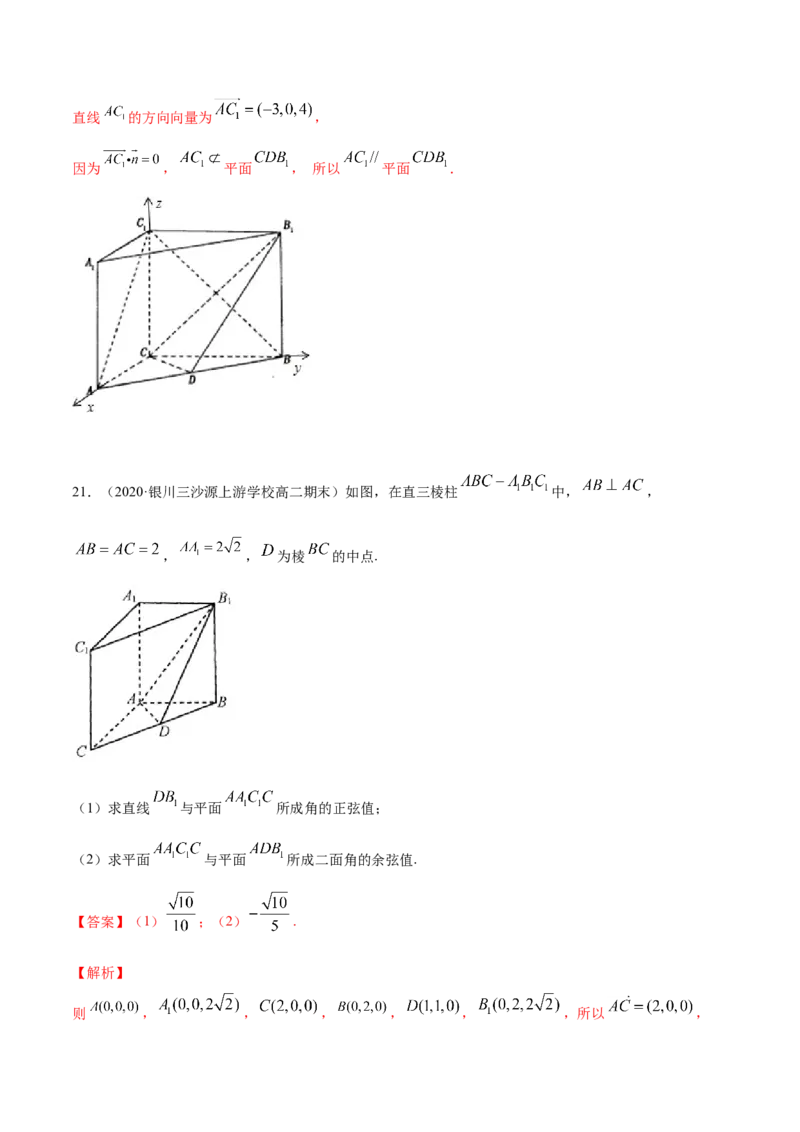
19.(2020·陕西省高二期末)如图,在棱长为2的正方体 中E,F分别为AB, 的
中点.(1)求 ;
(2)求证: 平面
【答案】(1) ;(2)证明见解析
【解析】
(1)由题知, , ,
∴ ,
∴
(2)由题知, , ,∴ ,
∴ ,故 ,
又 平面 , 平面
∴EF∥平面 .
20.(2020·北京高二期末)如图,在直三棱柱 中, , , , ,
点 是 的中点.
(1)求异面直线 与 所成的角;
(2)求证: 平面 .【答案】(1) (2)证明见解析
【解析】
(1)因为 , , ,
所以 ,所以 是直角三角形,
所以 ,所以
因为三棱柱 为直三棱柱,所以 平面 ,
所以 ,
以 为原点,分别以 、 、 为 轴、 轴、 轴,建立空间直角坐标系,
则 ,0, , ,0, , ,4, , ,0,
所以直线 的方向向量为 ,直线 的方向向量为 ,
设异面直线 与 所成的角为 ,
因为 ,
所以 ,
所以异面直线 与 所成的角为 .
(2)由(1)可知 , ,4, ,则 ,
设平面 的法向量为 ,则 ,所以
令 ,则 , ,所以直线 的方向向量为 ,
因为 , 平面 , 所以 平面 .
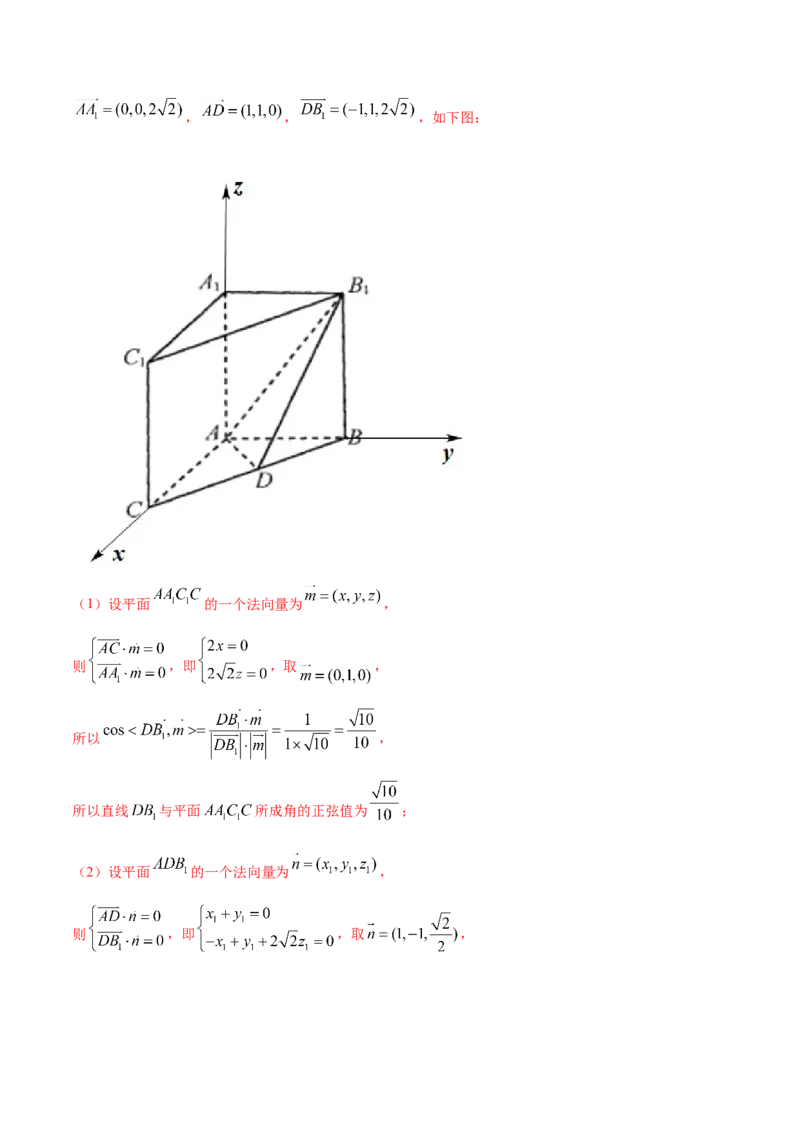
21.(2020·银川三沙源上游学校高二期末)如图,在直三棱柱 中, ,
, , 为棱 的中点.
(1)求直线 与平面 所成角的正弦值;
(2)求平面 与平面 所成二面角的余弦值.
【答案】(1) ;(2) .
【解析】
则 , , , , , ,所以 ,, , ,如下图:
(1)设平面 的一个法向量为 ,
则 ,即 ,取 ,
所以 ,
所以直线 与平面 所成角的正弦值为 ;
(2)设平面 的一个法向量为 ,
则 ,即 ,取 ,所以 ,
所以求平面 与平面 所成二面角的余弦值 .
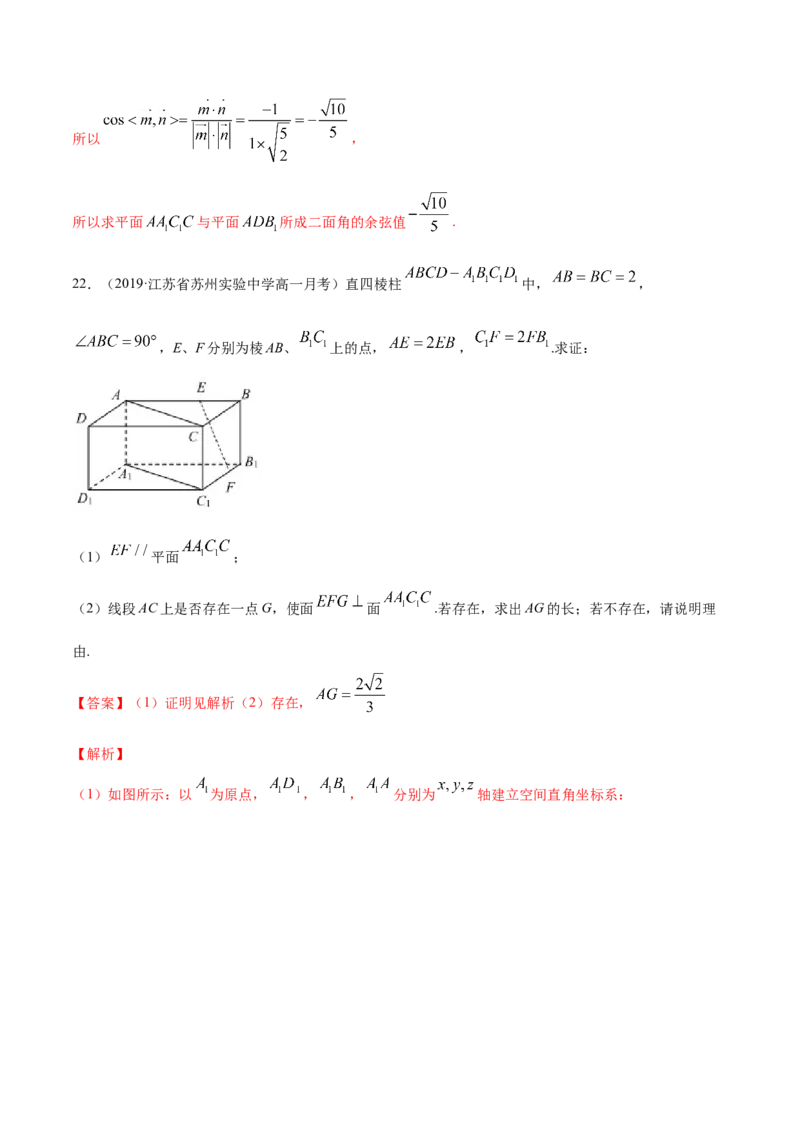
22.(2019·江苏省苏州实验中学高一月考)直四棱柱 中, ,
,E、F分别为棱AB、 上的点, , .求证:
(1) 平面 ;
(2)线段AC上是否存在一点G,使面 面 .若存在,求出AG的长;若不存在,请说明理
由.
【答案】(1)证明见解析(2)存在,
【解析】
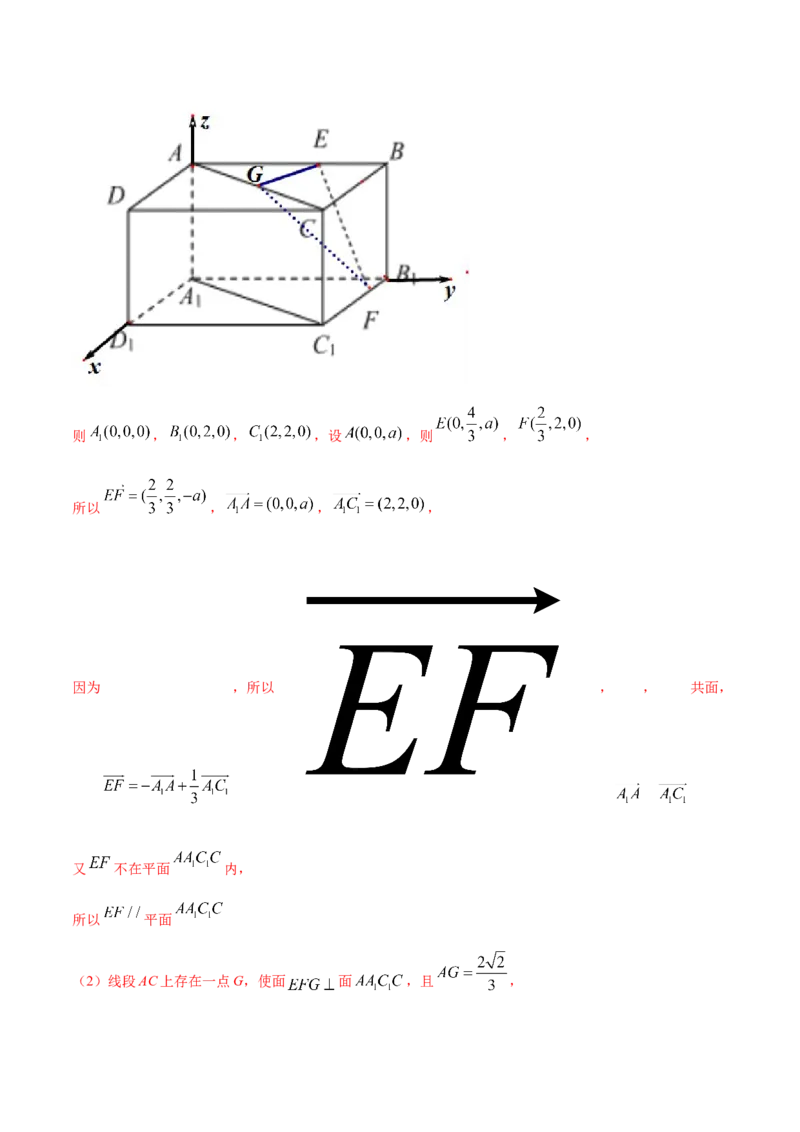
(1)如图所示:以 为原点, , , 分别为 轴建立空间直角坐标系:则 , , ,设 ,则 , ,
所以 , , ,
因为 ,所以 , , 共面,
又 不在平面 内,
所以 平面
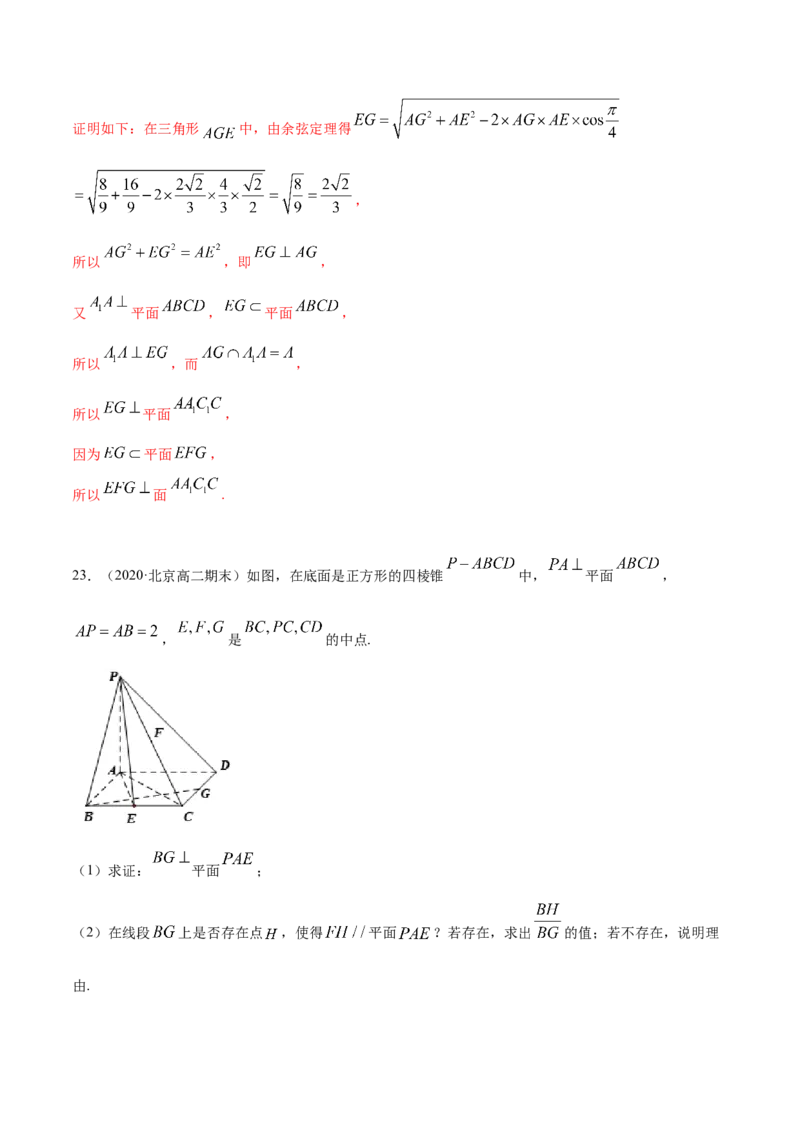
(2)线段AC上存在一点G,使面 面 ,且 ,证明如下:在三角形 中,由余弦定理得
,
所以 ,即 ,
又 平面 , 平面 ,
所以 ,而 ,
所以 平面 ,
因为 平面 ,
所以 面 .
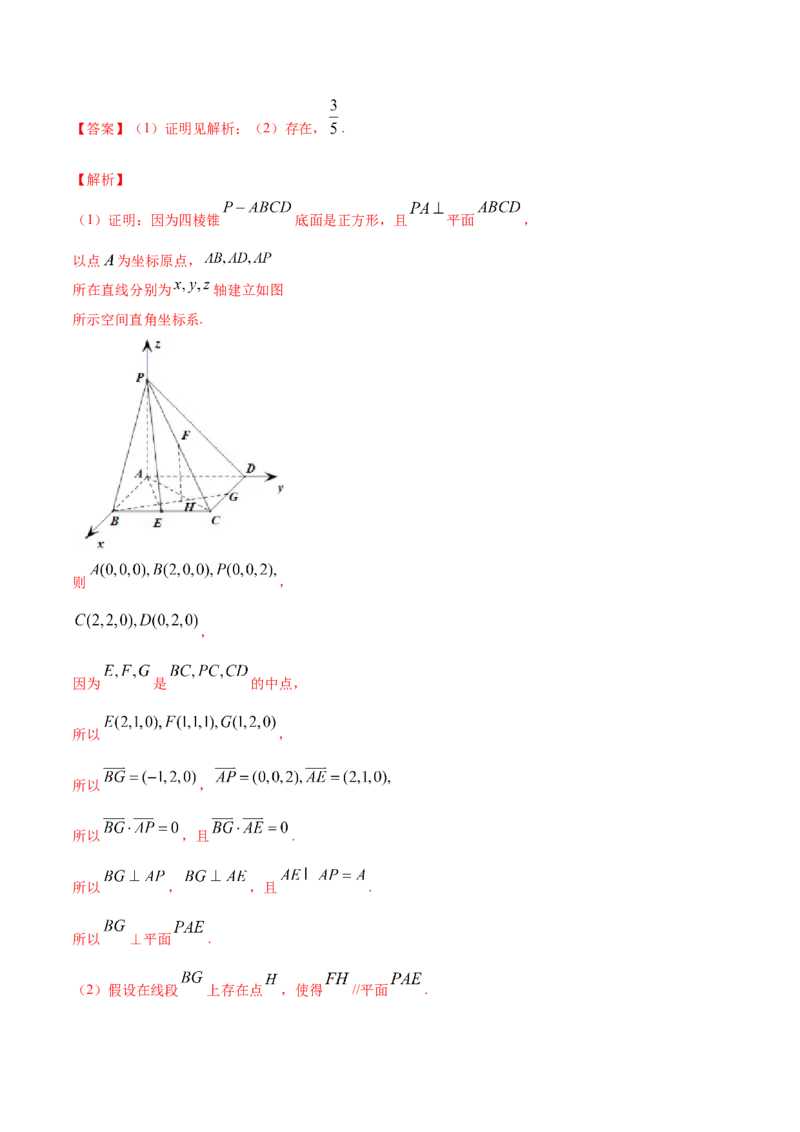
23.(2020·北京高二期末)如图,在底面是正方形的四棱锥 中, 平面 ,
, 是 的中点.
(1)求证: 平面 ;
(2)在线段 上是否存在点 ,使得 平面 ?若存在,求出 的值;若不存在,说明理
由.【答案】(1)证明见解析;(2)存在, .
【解析】
(1)证明:因为四棱锥 底面是正方形,且 平面 ,
以点 为坐标原点,
所在直线分别为 轴建立如图
所示空间直角坐标系.
则 ,
,
因为 是 的中点,
所以 ,
所以 ,
所以 ,且 .
所以 , ,且 .
所以 ⊥平面 .
(2)假设在线段 上存在点 ,使得 //平面 .设 ,
则 .
因为 //平面 , ⊥平面 ,
所以 .
所以 .
所以,在线段 上存在点 ,使得 //平面 .其中 .