文档内容
高二年级下学期期末仿真卷 05
本试卷共22题。全卷满分150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡
皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.记S 为等差数列{a}的前n项和,若a=3,a=9,则S 为( )
n n 2 5 6
A.36 B.32 C.28 D.24
2. 的展开式中的常数项为( )
A.﹣60 B.240 C.﹣80 D.180
3.设曲线 在 处的切线与直线y=ax+1平行,则实数a等于( )
A.﹣1 B. C.﹣2 D.2
4.在2019年高中学生信息技术测试中,经统计,某校高二学生的测试成绩 X~N(86,σ2),若已知P(80
<X≤86)=0.36,则从该校高二年级任选一名考生,他的测试成绩大于92分的概率为( )
A.0.86 B.0.64 C.0.36 D.0.14
5.设函数 ,若f(x)在点(3,f(3))的切线与x轴平行,且在区间[m﹣1,m+1]上单
调递减,则实数m的取值范围是( )
A.m≤2 B.m≥4 C.1<m≤2 D.0<m≤3
6.利用独立性检验的方法调查高中生的写作水平与喜好阅读是否有关,通过随机询问 120名高中生是否喜
好阅读,利用2×2列联表,由计算可得K2=4.236.
P 0.100 0.050 0.025 0.010 0.001
(K2≥k )
0
k 2.706 3.841 5.024 6.635 10.828
0
参照附表,可得正确的结论是( )A.有95%的把握认为“写作水平与喜好阅读有关”
B.有97.5%的把握认为“写作水平与喜好阅读有关”
C.有95%的把握认为“写作水平与喜好阅读无关”
D.有97.5%的把握认为“写作水平与喜好阅读无关”
7.某人设计一项单人游戏,规则如下:先将一棋子放在如图所示正方形 ABCD(边长为2个单位)的顶点A
处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为 i(i=1,
2,…,6),则棋子就按逆时针方向行走i个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又
回到点A处的所有不同走法共有( )
A.22种 B.24种 C.25种 D.27种
8.若两个等差数列{a},{b}的前 n 项和分别为 A 、B ,且满足 ,则 的值为
n n n n
( )
A. B. C. D.
二、多选题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项是符合题目要求
的,选对得分,错选或漏选不得分。
9.已知函数f(x)=xlnx,若0<x<x,则下列结论正确的是( )
1 2
A.xf(x)<xf(x) B.x+f(x)<x+f(x)
2 1 1 2 1 1 2 2
C. D.当lnx>﹣1时,xf(x)+xf(x)>2xf(x)
1 1 2 2 2 1
10.等差数列{a}的前n项和为S,若a<0,a >0,则下列结论正确的是( )
n n 9 10
A.S >S B.S <0 C.S >S D.S >0
10 9 17 18 19 19
11.已知 的展开式中各项系数的和为2,则下列结论正确的有( )
A.a=1
B.展开式中常数项为160
C.展开式系数的绝对值的和1458D.若r为偶数,则展开式中xr和xr﹣1的系数相等
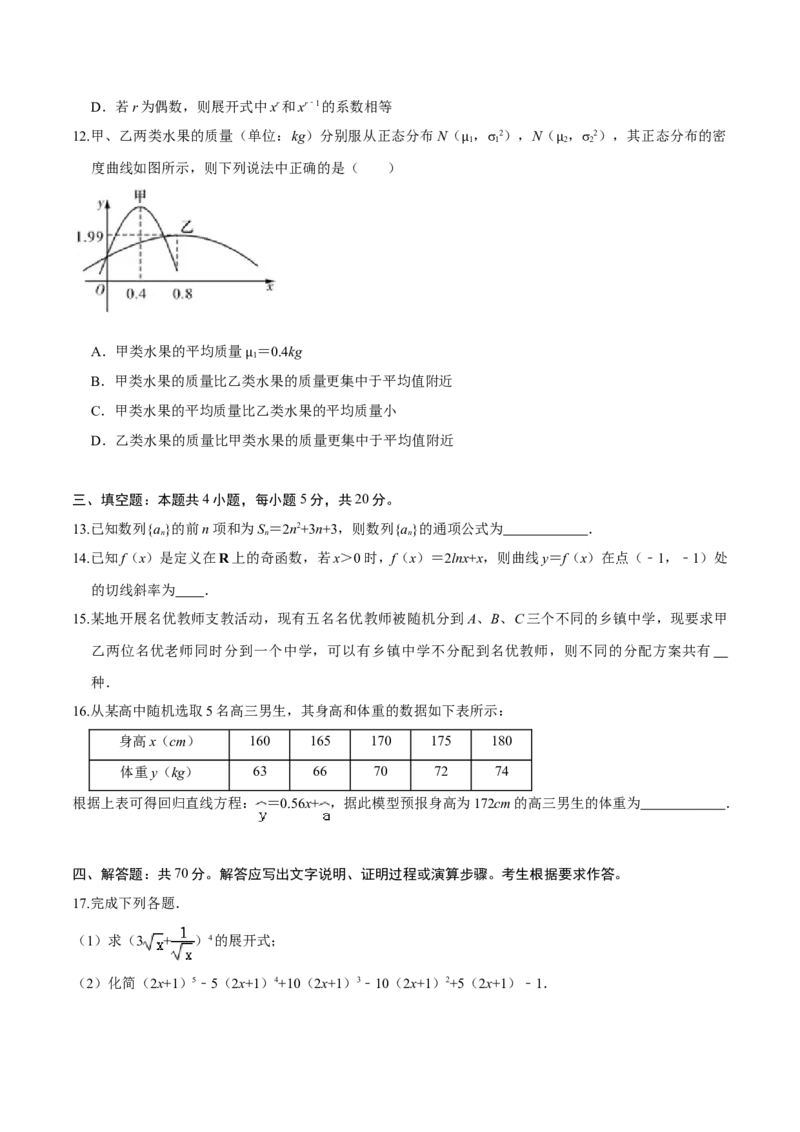
12.甲、乙两类水果的质量(单位:kg)分别服从正态分布N( ,σ2),N( ,σ2),其正态分布的密
1 1 2 2
度曲线如图所示,则下列说法中正确的是( ) μ μ
A.甲类水果的平均质量 =0.4kg
1
B.甲类水果的质量比乙类μ水果的质量更集中于平均值附近
C.甲类水果的平均质量比乙类水果的平均质量小
D.乙类水果的质量比甲类水果的质量更集中于平均值附近
三、填空题:本题共4小题,每小题5分,共20分。
13.已知数列{a}的前n项和为S=2n2+3n+3,则数列{a}的通项公式为 .
n n n
14.已知f(x)是定义在R上的奇函数,若x>0时,f(x)=2lnx+x,则曲线y=f(x)在点(﹣1,﹣1)处
的切线斜率为 .
15.某地开展名优教师支教活动,现有五名名优教师被随机分到A、B、C三个不同的乡镇中学,现要求甲
乙两位名优老师同时分到一个中学,可以有乡镇中学不分配到名优教师,则不同的分配方案共有
种.
16.从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
身高x(cm) 160 165 170 175 180
体重y(kg) 63 66 70 72 74
根据上表可得回归直线方程: =0.56x+ ,据此模型预报身高为172cm的高三男生的体重为 .
四、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。考生根据要求作答。
17.完成下列各题.
(1)求(3 + )4的展开式;
(2)化简(2x+1)5﹣5(2x+1)4+10(2x+1)3﹣10(2x+1)2+5(2x+1)﹣1.18.已知函数f(x)=x3+ax2+bx+2,若y=f(x)在 有极值,且f(x)在点(1,f(1))处的切线斜
率为﹣5.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[0,3]上的最大值和最小值.
19.在数列{a}中,已知a>0,a=1,a 2﹣a2﹣a ﹣a=0.
n n 1 n+1 n n+1 n
(1)求证:数列{a}是等差数列;
n
(2)设数列{a}的前n和为S,b= ,求数列{b}的前n和T.
n n n n n20.某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如表:
质量指标值m 25≤m<35 15≤m<25或35≤m< 0<m<15或45≤m<
45 65
等级 一等品 二等品 三等品
某企业从生产的这种产品中抽取100件产品作为样本,检测其质量指标值,得到右
图的率分布直方图.(同一组数据用该区间的中点值作代表)
(1)该企业为提高产品质量,开展了质量提升月”活动,活动后再抽样
检测,产品三等品数Y近似满足Y~H(10,15,100),请测算“质量提升月”活动后这种产品的“二等
品率“(一、二等品其占全部产品百分比)较活动前提高多少个百分点?
(2)若企业每件一等品售价180元,每件二等品售价150元,每件三等品售价120元,以样本中的频率代
替相应概率,现有一名联客随机购买两件产品,设其支付的费用为 X(单位:元),求X的分布列及数学
期望.
21.伴随着科技的发展,人们的生活节奏也越来越快.听书,逐渐成为了爱阅读的人们的一种喜好,付费阅
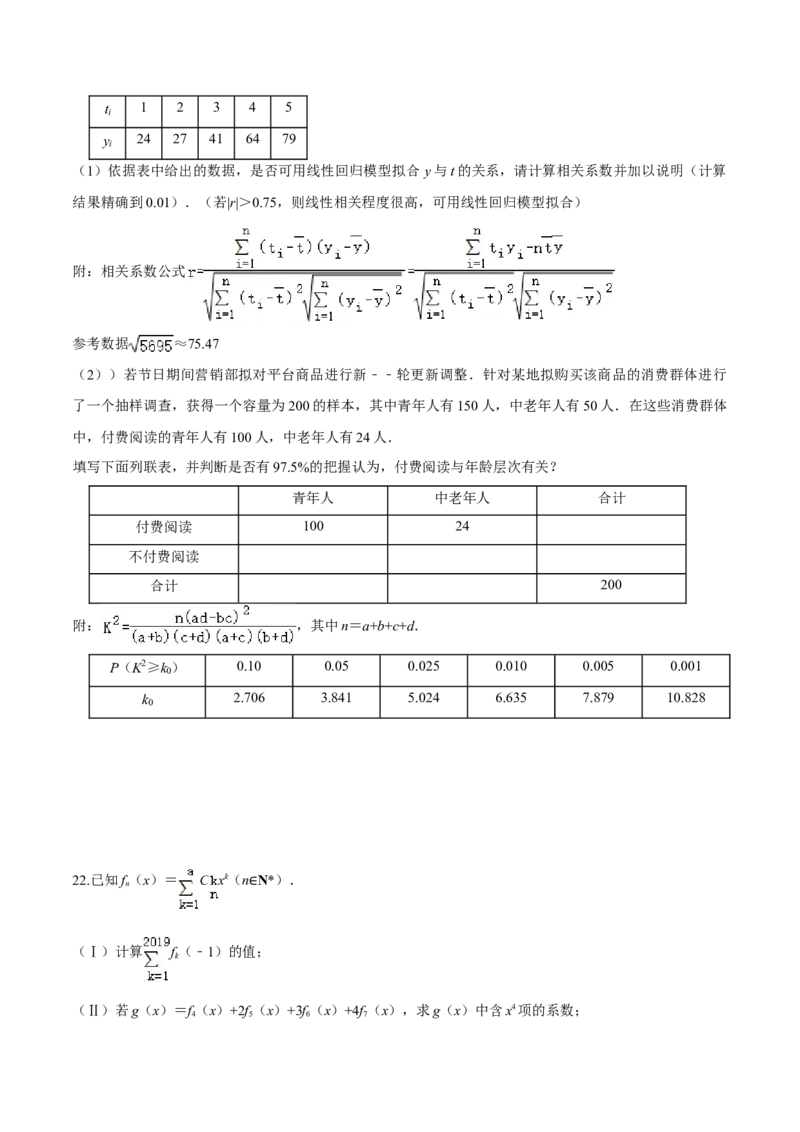
读也成为追求更高价值的途径之一.某网络公司组织统计了近五年来该公司参与付费听书的人数 y;
(单位:人)与时间t(单位:年)的数据,列表如下:t 1 2 3 4 5
i
y 24 27 41 64 79
i
(1)依据表中给出的数据,是否可用线性回归模型拟合 y与t的关系,请计算相关系数并加以说明(计算
结果精确到0.01).(若|r|>0.75,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式
参考数据 ≈75.47
(2))若节日期间营销部拟对平台商品进行新﹣﹣轮更新调整.针对某地拟购买该商品的消费群体进行
了一个抽样调查,获得一个容量为200的样本,其中青年人有150人,中老年人有50人.在这些消费群体
中,付费阅读的青年人有100人,中老年人有24人.
填写下面列联表,并判断是否有97.5%的把握认为,付费阅读与年龄层次有关?
青年人 中老年人 合计
付费阅读 100 24
不付费阅读
合计 200
附: ,其中n=a+b+c+d.
P(K2≥k ) 0.10 0.05 0.025 0.010 0.005 0.001
0
k 2.706 3.841 5.024 6.635 7.879 10.828
0
22.已知f(x)= C xk(n N*).
n
∈
(Ⅰ)计算 f(﹣1)的值;
k
(Ⅱ)若g(x)=f(x)+2f(x)+3f(x)+4f(x),求g(x)中含x4项的系数;
4 5 6 7(Ⅲ)证明: = .