文档内容
拓展一 利用递推公式求通项公式常用方法
【题组一 累加法】
1.如果数列 满足: ,则 ( )
A. B. C. D.
【答案】C
【解析】由题意可得, ,
,
,…
,
以上 个式子相加可得,
,
,故选B.
2.(2020·河北新华·石家庄二中高二月考)在数列 中, , ,则 的通
项公式为( ).
A. B.
C. D.
【答案】A
【解析】由已知得 ,
所以将上述 个式子相加,整理的
又因为 ,所以 .
故选A.
3.(2020·赣州市赣县第三中学高一期中)已知数列 满足 , ,则 ( )
A. B. C. D.
【答案】B
【解析】 数列 满足 , ,
,
,
,
,
……
,
累加得: ,
又 ,
,.
故选B.
【题组二 累乘法】
1.(2020·吉林南关·长春市实验中学高一月考(理))已知数列 满足 ,
.数列 的通项公式是______.
【答案】
【解析】 ,
当 时,
当 时,
,
两式相减得: ,即 ,
,
,
,
,累乘得: ,所以 ,
,
故答案为:
【题组三 公式法】
1.(2020·河北高一期末)数列{a}的前n项和为S,若 则 ____________ .
n n
【答案】 .
【解析】 时, 时, ,可得 ,即
数列 从第二项起为等比数列, 时, ,故答案为 .
2.(2020·祁县第二中学校)数列 满足, ,写出数列 的通
项公式__________.
【答案】
【解析】因为 ,所以,两式相减得 ,即 ,
又 ,所以 ,因此
3.(2020·江西南康中学月考(文))数列 的前 项和 ,则该数列的通项公式为
__________.
【答案】
【解析】 当 时
当 时也适合,故 .即答案为 .
4.(2020·宜城市第二高级中学)若数列{a }的前n项和为S= a+ ,则数列{a }的通项公式是
n n n n
a=______.
n
【答案】 ;
【解析】当n=1时,a=S = a+ ,解得a=1,当n≥2时,a=S -S =( )-( )= -
1 1 1 1 n n n-1
整理可得 a=− a ,即 =-2,故数列{a }是以1为首项,-2为公比的等比数列,故a=1×
n n−1 n n
(-2)n-1=(-2)n-1故答案为(-2)n-1.
5.(2020·陕西延安中学高三期末)数列{a}满足 ,则aaa…
n 1 2 3
a =( )
10A. B. C. D.
【答案】A
【解析】n=1时,a= ,
1
∵ ,
∴ 时, ,
两式相减可得2n-1a= ,
n
∴ ,
n=1时,也满足
∴ ,
故选A
6.(2020·甘肃省岷县第一中学(文))如果数列 的前 项和为 ,则这个数列的通项公
式是( )
A. B. C. D.
【答案】B
【解析】由 ,
当 时, ,
所以 ,当 时, ,此时 ,
所以,数列 是以 为首项, 为公比的等比数列,即 .
故选:B.
【题组四 倒数法】
1.(2020·全国高三课时练习(理))在数列{ }中,已知 , , ,则 等于
( )
A. B. C. D.
【答案】B
【解析】将等式 两边取倒数得到 , 是公差为 的等差数
列, = ,根据等差数列的通项公式的求法得到 ,故 = .
故答案为:B.
2.(2019·浙江省宁波市鄞州中学)已知数列 满足 ,那么 等于( )
A. B. C. D.
【答案】D
【解析】 ,
,即 ,
又 所以数列 是首项为 ,公差为 的等差数列,,
,故 ,
故选:D.
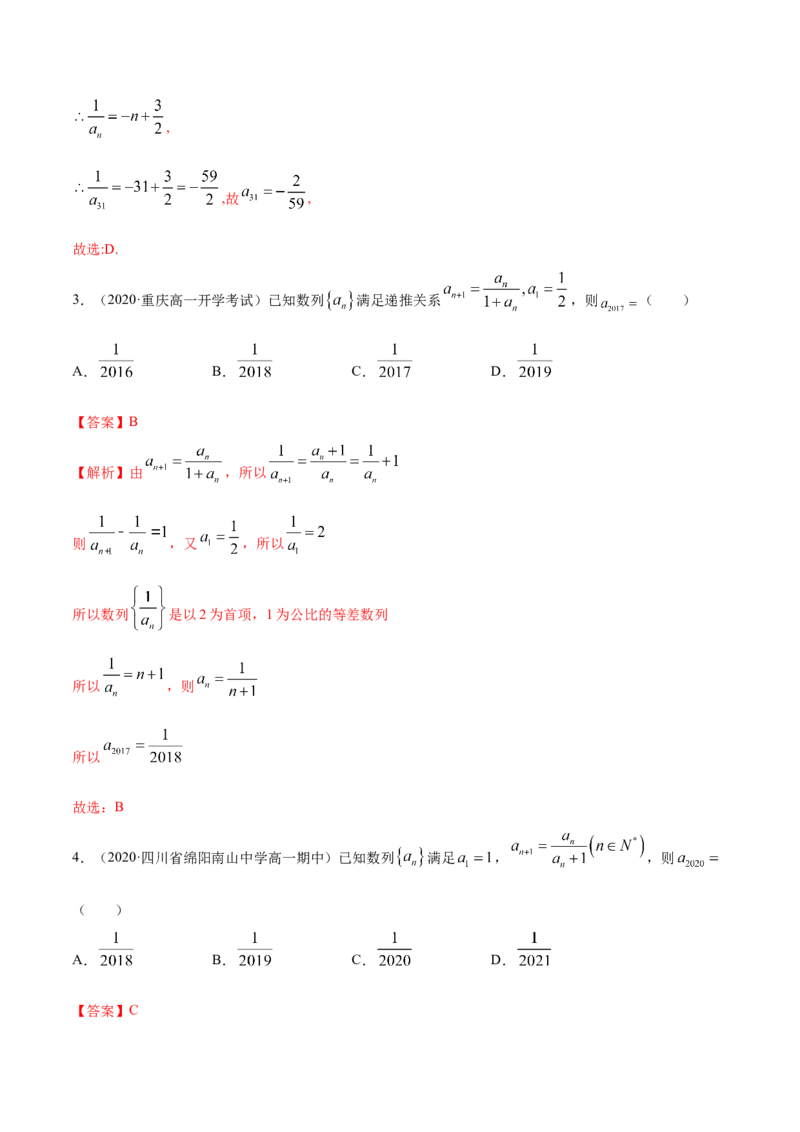
3.(2020·重庆高一开学考试)已知数列 满足递推关系 ,则 ( )
A. B. C. D.
【答案】B
【解析】由 ,所以
则 ,又 ,所以
所以数列 是以2为首项,1为公比的等差数列
所以 ,则
所以
故选:B
4.(2020·四川省绵阳南山中学高一期中)已知数列 满足 , ,则
( )
A. B. C. D.
【答案】C【解析】 ,
两边同时取倒数得 ,
即 ,
即数列 是公差 的等差数列,首项为 .
则 ,
得 ,
则 ,
故选:
【题组五 周期数列】
1.(2020·河南高二月考(理))在数列 中, , ( , ),则
( )
A. B.1
C. D.2
【答案】A
【解析】 , , ,
可得数列 是以3为周期的周期数列, .故选:A.2.(2020·呼图壁县第一中学期末)已知数列 中, , ( ),那么
等于( )
A. B. C.2 D.4
【答案】B
【解析】因为 , ,
所以 ,
,
,
…
所以数列 是以3为周期的数列,
所以 ,
故选:B
3.(2020·河北路南·唐山一中高一月考)已知数列 中, ,则
( )
A. B. C. D.
【答案】B
【解析】因为 ,①则 ,②①+②有: ,即 ,则 ,
即数列 的周期为6,
又 ,得 , ,
则 ,
故选:D.