文档内容
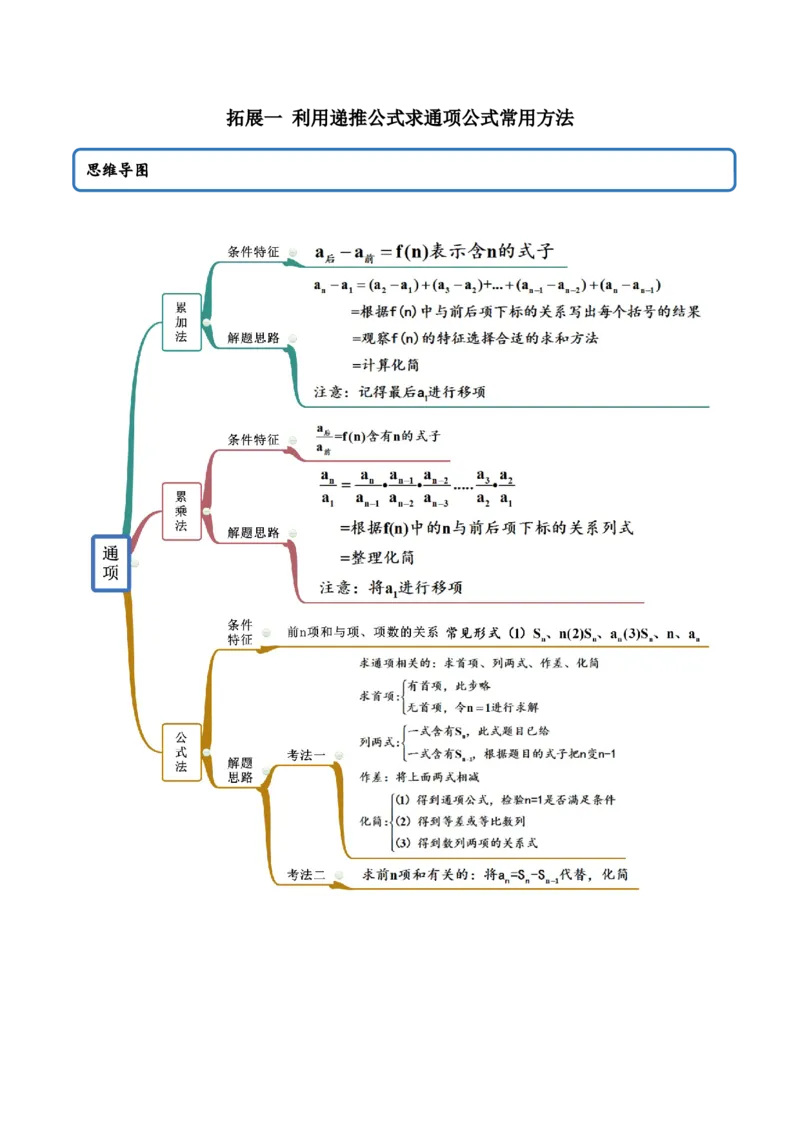
拓展一 利用递推公式求通项公式常用方法
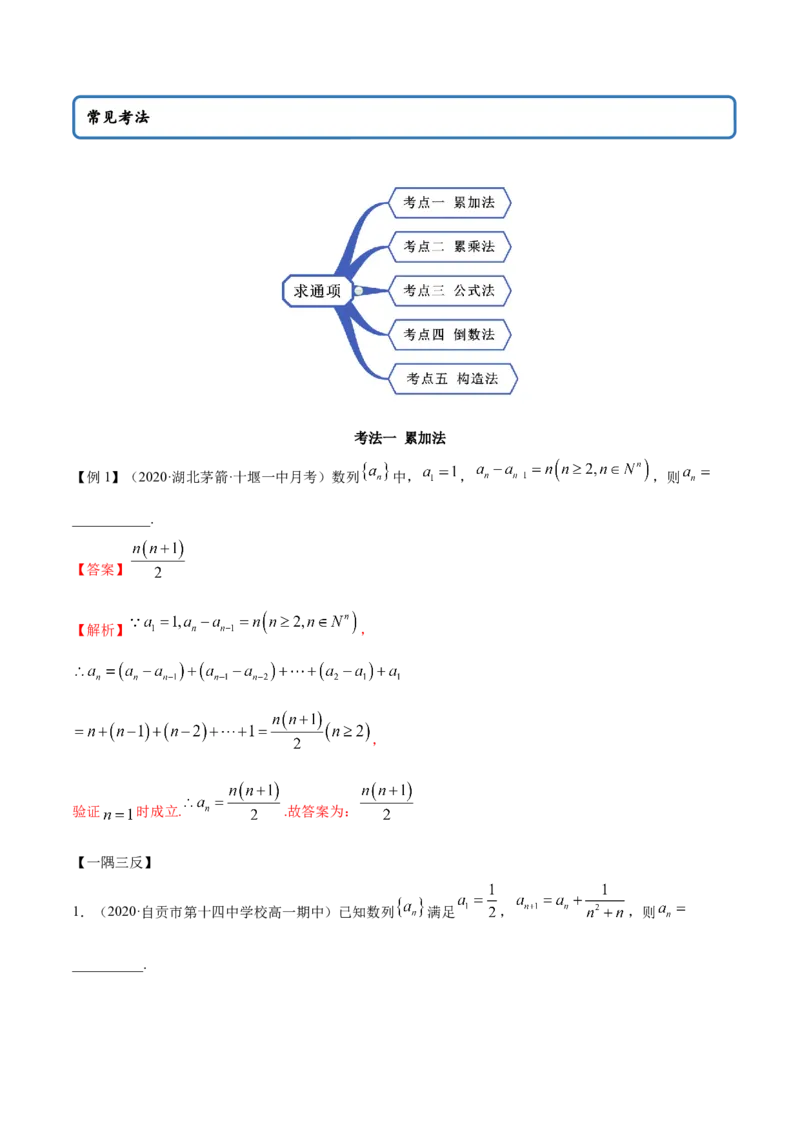
思维导图常见考法
考法一 累加法
【例1】(2020·湖北茅箭·十堰一中月考)数列 中, , ,则
___________.
【答案】
【解析】 ,
,
验证 时成立. .故答案为:
【一隅三反】
1.(2020·自贡市第十四中学校高一期中)已知数列 满足 , ,则
__________.【答案】
【解析】因为 ,所以 ,
则当 时, ,将 个式子相加可得
,因为 ,则 ,
当 时, 符合题意,所以 .
故答案为: .
2.(2020·吉林朝阳·长春外国语学校高二开学考试)设数列 中, ,则通项
___________.
【答案】
【解析】∵ ∴ , ,
, , , ,
将以上各式相加得:
故应填 ;考法二 累乘法
【例2】.(2020·安徽省泗县第一中学开学考试)已知 , ,则数列
的通项公式是( )
A. B. C. D.
【答案】D
【解析】由 得: ,即 ,
则 , , ,…….., ,
由累乘法可得 ,又因为 ,所以 .
故选:D.
【一隅三反】
1.(2020·黑龙江伊春二中高一期中)已知 , ,则数列 的通项公式 等于(
)
A. B. C. D.
【答案】C
【解析】
当n≥2时, ,
经检验, 也符合上述通项公式.
本题选择C选项.
2.(2020·横峰中学开学考试(理))在数列 中, , ,则______.
【答案】
【解析】由题意得:当 时, ,所以 ,即
,
也即是 ,所以 ,
所以 ,故答案为: .
考法三 公式法
【例3】(1)(2020·湖北沙区·沙市中学期末)已知数列{a}的前n项和S=n2+n,则a=_____.
n n n
(2)(2020·江西省信丰中学月考)若数列的前 项和 ,则的通项公式是 ________
【答案】(1)2n(2)
【解析】(1)由题,当 时, ,
当 时, .当 时也满足.故 .故答案为:
(2)当n=1时, ,解得 ,
当n≥2时, ,
整理可得 ,即 ,故数列 以 为首项, 为公比的等比数列,所以 ,故答案为: .
【一隅三反】
1.(2020·上海市实验学校高一期末)数列 的前n项和 ,则其通项公式 ________ .
【答案】
【解析】当 时, ;
当 时, ;
故 故答案为:
2.(2020·山西大同·一模(文))已知 为数列 的前 项和,若 ,则数列
的通项公式为___________.
【答案】
【解析】 为数列 的前 项和, ①
时, ②
① ②,得: ,
,
,
数列 的通项公式为 .故答案为: .
3.(2020·尤溪县第五中学高一期末).已知数列 满足 ,则
的通项公式___________________.
【答案】a=3•2n﹣2
n
【解析】∵数列{a}满足2a+22a+23a+…+2na=4n﹣1,
n 1 2 3 n
∴当n≥2时,2na=(4n﹣1)﹣(4n﹣1﹣1),化为a=3•2n﹣2.
n n
当n=1时,2a=4﹣1,解得 ,上式也成立.∴a=3•2n﹣2.
1 n
故答案为a=3•2n﹣2.
n
考法四 倒数法
【例4】(2020·南充西南大学实验学校高一月考)若数列 满足 ,且 ,则
___________.
【答案】
【解析】 ,即
数列 是以 为首项, 为公差的等差数列
故答案为:
【一隅三反】
1.(2020·四川高一期末)设数列 的前n项和 满足 ,且 ,则
_____.【答案】
【解析】由 ,得
是以 为首相,1为公差的等差数列,
,
,
当 时, ,
故答案为:
3.(2020·四川成都)若数列 满足 ( , ),且 ,则 ( )
A. B. C. D.
【答案】A
【解析】当 且 ,在等式 两边取倒数得 ,
,且 ,所以,数列 为等差数列,且首项为 ,公差为 ,因此, . 故选:A.
考法五 构造法
【例5】(2020·双峰县第一中学高二开学考试)数列 中,若 , ,则该数
列的通项 ( )
A. B. C. D.
【答案】A
【解析】因为 ,所以 ,
即数列 是以4为首项,2为公比的等比数列,所以 ,
故 ,故选:A
【一隅三反】
1.(2020·贵州省思南中学月考)已知数列 中, 则 ___________.
【答案】
【解析】因为 ,所以 且 ,
所以 ,所以 是以 为首项, 为公比的等比数列,
所以 ,所以 ,
故答案为: .
2.(2019·兴安县第三中学高二期中)已知数列 满足 ,则 的通项公式为
__________________.
【答案】【解析】因为 , ,所以 ,即
所以 以 为首项, 为公比的等比数列,所以
所以 故答案为: