文档内容
2023—2024 学年(下)安徽高一期末质量检测
数学
考生注意:
1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上,并将考生号条形码粘贴
在答题卡上的指定位置.
2.回答选择题时,选出每小题答案 后,用铅笔把答题卡对应题目的答案 标号涂黑.如需改
动,用橡皮擦干净后,再选涂其他答案 标号.回答非选择题时,将答案 写在答题卡上.与在
本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. 复数 在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知向量 , , ,若 与 共线,则实数 ( )
A. B. C. D. 0
3. 2024年全国夏季游泳锦标赛将在合肥举办,某高中共有男学生1300人,女学生1100人,男教师150人,
女教师100人申请做志愿者,现按人数比例用分层随机抽样的方法从中抽取部分人,若抽取的人中男性有
290人,则抽取的总人数为( )
A. 480 B. 500 C. 520 D. 530
4. 已知在梯形 中, , , ,若 ,则( )
A. , B. ,
C. , D. ,
的
5. 从 , ,1,3这4个数中随机取出2个不同 数,则这2个数的乘积不超过1的概率为( )
第1页/共8页
学科网(北京)股份有限公司A. B. C. D.
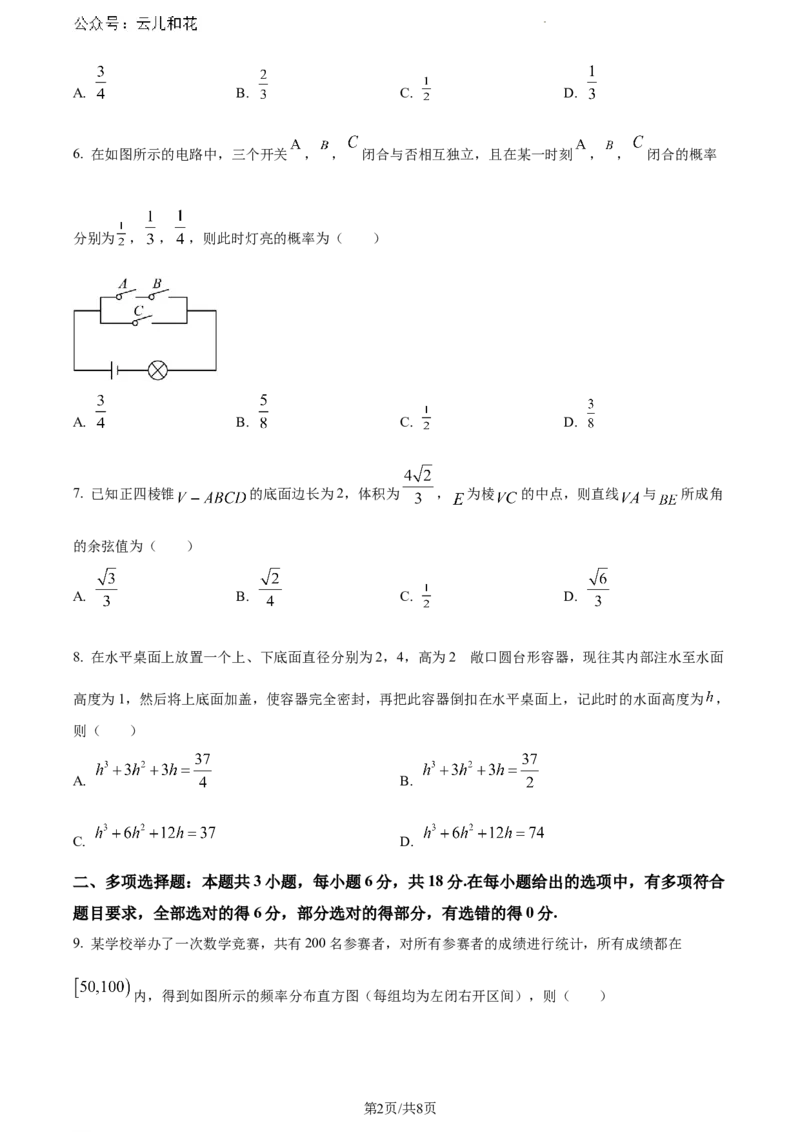
6. 在如图所示的电路中,三个开关 , , 闭合与否相互独立,且在某一时刻 , , 闭合的概率
分别为 , , ,则此时灯亮的概率为( )
A. B. C. D.
7. 已知正四棱锥 的底面边长为2,体积为 , 为棱 的中点,则直线 与 所成角
的余弦值为( )
A. B. C. D.
的
8. 在水平桌面上放置一个上、下底面直径分别为2,4,高为2 敞口圆台形容器,现往其内部注水至水面
高度为1,然后将上底面加盖,使容器完全密封,再把此容器倒扣在水平桌面上,记此时的水面高度为 ,
则( )
A. B.
C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求,全部选对的得6分,部分选对的得部分,有选错的得0分.
9. 某学校举办了一次数学竞赛,共有200名参赛者,对所有参赛者的成绩进行统计,所有成绩都在
内,得到如图所示的频率分布直方图(每组均为左闭右开区间),则( )
第2页/共8页
学科网(北京)股份有限公司.
A
B. 所有参赛者成绩的极差小于50
C. 估计所有参赛者成绩的中位数为70.5
D. 成绩在区间 内的人数为64
10. 设 , ,则下列结论中正确的是( )
A. 若 ,则 B. 若 ,则
.
C 若 ,则 D. 若 ,则
11. 在三棱锥 中,若 , , 分别为棱 , , 的中点,平面 、平面 、平
面 相交于 点,则( )
A. B.
C. D.
三、填空题:本题共3小题,每小题5分,共15分.
12. 若向量 , ,则 在 上的投影向量的坐标为______.
13. 已知一个高为3的圆锥的底面圆周和顶点都在一个半径为2的球的球面上,设圆锥和球的体积分别为
, ,则 ______.
14. 已知在 中, , , , 为线段 的延长线上一点, 的
第3页/共8页
学科网(北京)股份有限公司平分线所在的直线与直线 交于点 ,则 ______.
参考数据: .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 在 中,设向量 , ,且 , .
(1)求 的值;
(2)若 ,求 .
16. 某校高一(1)班、(2)班的学生人数分别为40,42,在某次测验中,记(1)班所有学生的成绩分
别为 , ,…, ,平均成绩为 ,方差为 ,已知 , .
(1)求 , ;
(2)记(2)班所有学生的成绩分别为 , ,…, ,其平均成绩为82, ,试求两
个班的所有学生的平均成绩(结果保留整数),并说明哪一个班的成绩比较稳定.
17. 某公司拟通过摸球抽奖的方式对员工发放生日红包.先在一个不透明的袋子中装入7个标有一定金额的
球(除标注的金额不同外,其余均相同),其中标注的金额为100元、200元、300元的球分别有2个、2
个、3个.参与的员工每次从袋中随机摸出1个球,记录球上标注的金额后放回袋中,连续摸 次.规定:某
员工摸出的球上所标注的金额之和为其所获得的生日红包的总金额.
(1)当 时,求甲员工所获得的生日红包总金额不低于200元的概率;
(2)当 时,设事件 “甲员工获得的生日红包总金额不超过400元”,事件 “甲员工获得的
生日红包总金额不低于300元”,试判断事件 , 是否相互独立,并说明理由.
18. 在 中,角 , , 的对边分别为 , , ,已知 .
第4页/共8页
学科网(北京)股份有限公司(1)求 ;
(2)如图, 为 的外接圆 的 上一动点(含端点), .
(ⅰ)求 的取值范围;
(ⅱ)当 且点 不重合时,求 .
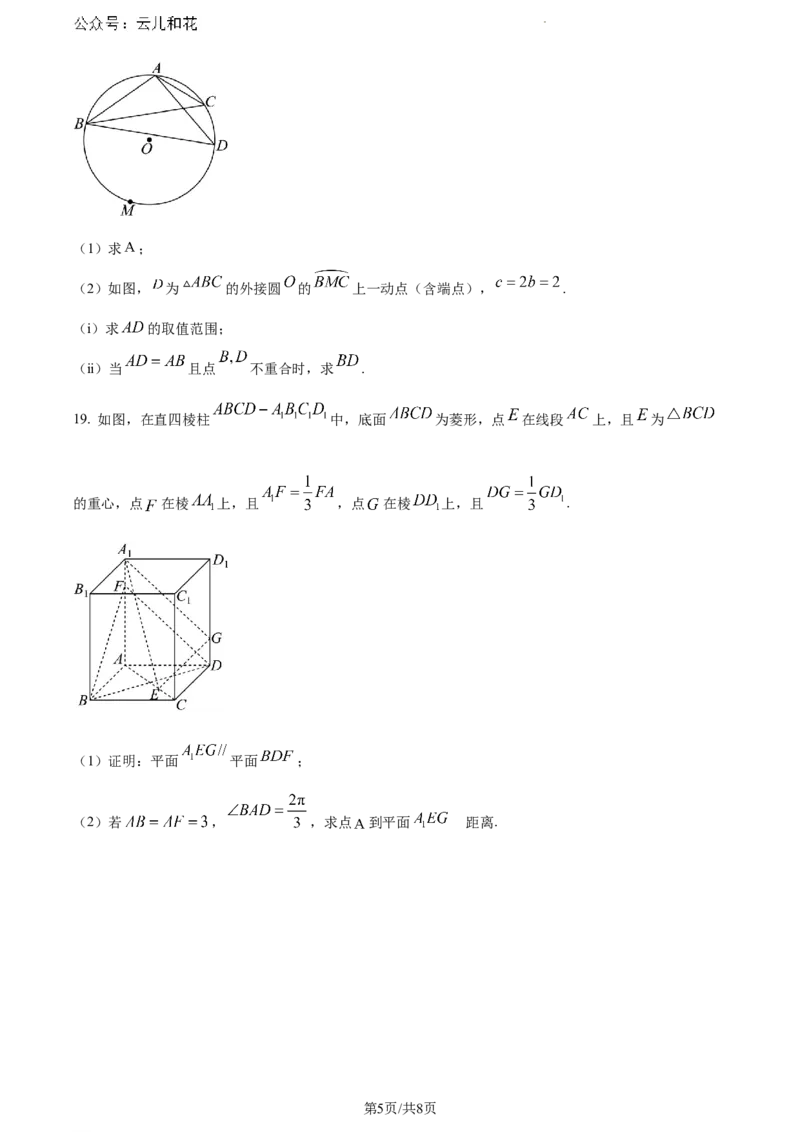
19. 如图,在直四棱柱 中,底面 为菱形,点 在线段 上,且 为
的重心,点 在棱 上,且 ,点 在棱 上,且 .
(1)证明:平面 平面 ;
(2)若 , ,求点 到平面 的距离.
第5页/共8页
学科网(北京)股份有限公司2023—2024 学年(下)安徽高一期末质量检测
数学
考生注意:
1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上,并将考生号条形码粘贴
在答题卡上的指定位置.
2.回答选择题时,选出每小题答案 后,用铅笔把答题卡对应题目的答案 标号涂黑.如需改
动,用橡皮擦干净后,再选涂其他答案 标号.回答非选择题时,将答案 写在答题卡上.与在
本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
【1题答案】
【答案】C
【2题答案】
【答案】B
【3题答案】
【答案】D
【4题答案】
【答案】A
【5题答案】
【答案】B
【6题答案】
【答案】D
【7题答案】
【答案】A
【8题答案】
【答案】C
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求,全部选对的得6分,部分选对的得部分,有选错的得0分.
【9题答案】
第6页/共8页
学科网(北京)股份有限公司【答案】BCD
【10题答案】
【答案】BC
【11题答案】
【答案】ACD
三、填空题:本题共3小题,每小题5分,共15分.
【12题答案】
【答案】
【13题答案】
【答案】
【14题答案】
【答案】
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
【15题答案】
【答案】(1)5 (2)
【16题答案】
【答案】(1) ,
(2)81,(1)班的成绩比较稳定
【17题答案】
【答案】(1)
(2)不相互独立,理由见解析
【18题答案】
【答案】(1)
第7页/共8页
学科网(北京)股份有限公司(2)(i) ;(ii)
【19题答案】
【答案】(1)证明见解析
(2)
第8页/共8页
学科网(北京)股份有限公司