文档内容
期中测试卷 02
(本卷满分150分,考试时间120分钟)
(人教A版2019)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符
合题目要求的.
1.已知平面向量 , ,若存在实数 ,使得 ,则实数 的值为( )。
A、
B、
C、
D、
【答案】D
【解析】∵ ,∴ ,则 ,解得 或 ,
又 ,∴ ,∴ ,故选D。
2.下列说法中错误的是( )。
A、两条平行线段在直观图中对应的两条线段仍然平行
B、平行于坐标轴的线段长度在直观图中仍然保持不变
C、平行于坐标轴的线段在直观图中仍然平行于坐标轴
D、斜二测坐标系取的角可能是
【答案】B
【解析】平行于 轴的线段在直观图中变为原来的一半,故B错误,
由斜二测画法的基本要求可知A、C、D正确,故选B。
3.在下列命题中,正确命题的个数为( )。
①两个复数不能比较大小;
②若 是纯虚数,则实数 ;
③ 是虚数的一个充要条件是 ;
④若 、 是两个相等的实数,则 是纯虚数;
⑤ 的一个充要条件是 ;
⑥ 的充要条件是 。
A、
B、
C、D、
【答案】B
【解析】复数为实数时,可以比较大小,①错,
时, ,②错,
为实数时,也有 ,③错,
时, ,④错,
⑤⑥正确,
故选B
4.设 、 是两个不同的平面,则 的充要条件是( )。
A、平面 内任意一条直线与平面 垂直
B、平面 、 都垂直于同一条直线
C、平面 、 都垂直于同一平面
D、平面 内存在一条直线与平面 垂直
【答案】D
【解析】若 ,则平面 内存在直线与平面 不垂直,选项A不正确;
若平面 、 都垂直于同一条直线,则平面 与 平行,选项B不正确;
若平面 、 都垂直于同一平面,则平面 、 可以平行,也可以相交,选项C不正确;
若平面 内存在一条直线与平面 垂直,则根据面面垂直的判定定理,可知 ,
若 ,则由面面垂直的性质定理知,
平面 内垂直于两个平面的交线的直线一定垂直于平面 ,故选项D正确;
故选D。
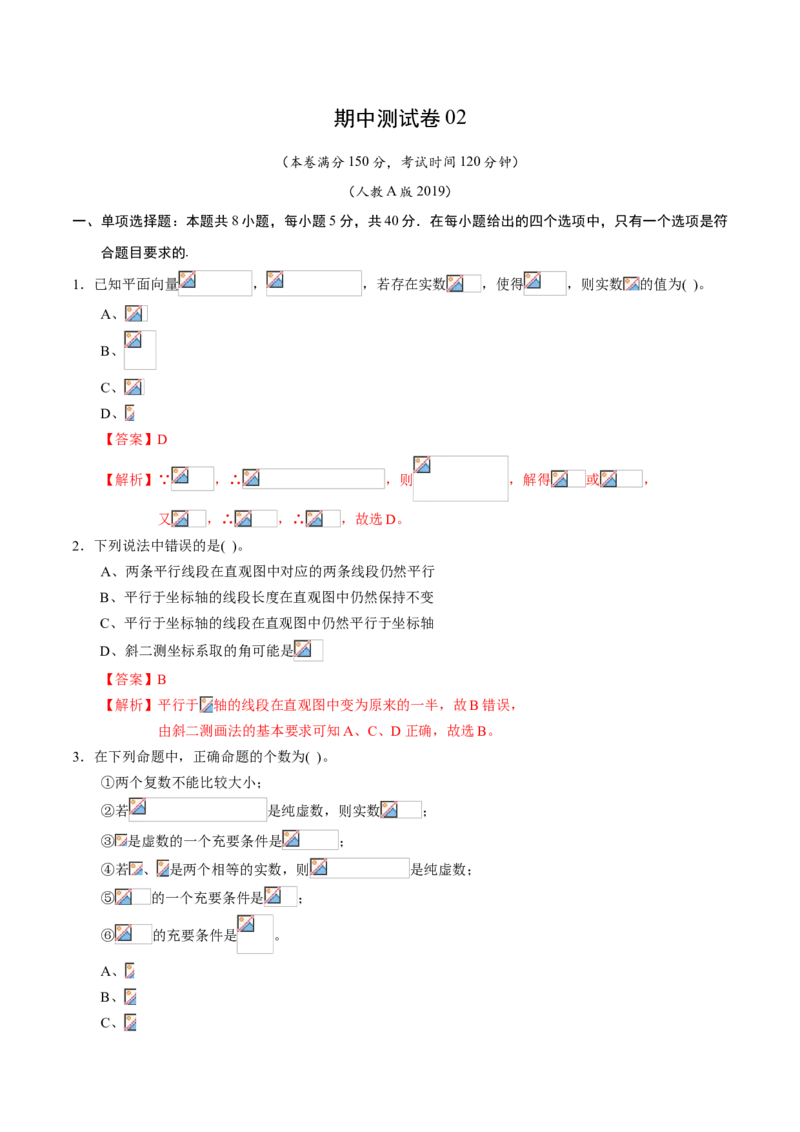
5.如图,在长方体 中,用截面截下一个棱锥 ,则棱锥 的体积与剩
余部分的体积之比为( )。
A、
B、
C、
D、
【答案】A
【解析】设 , , ,则长方体 的体积 ,
又 ,且三棱锥 的高为 ,
∴ ,则剩余部分的几何体体积 ,
则 ,故选A。6.四面体 中, , , ,则四面体 外接
球的表面积为( )。
A、
B、
C、
D、
【答案】C
【解析】将四面体 置于一个长方体中,
∴四面体 的外接球即为长方体的外接球,
设长方体的长、宽、高分别为 、 、 ,则根据图形可有 ,
则外接球的直径 ,∴ ,
则球的表面积为 ,故选C。
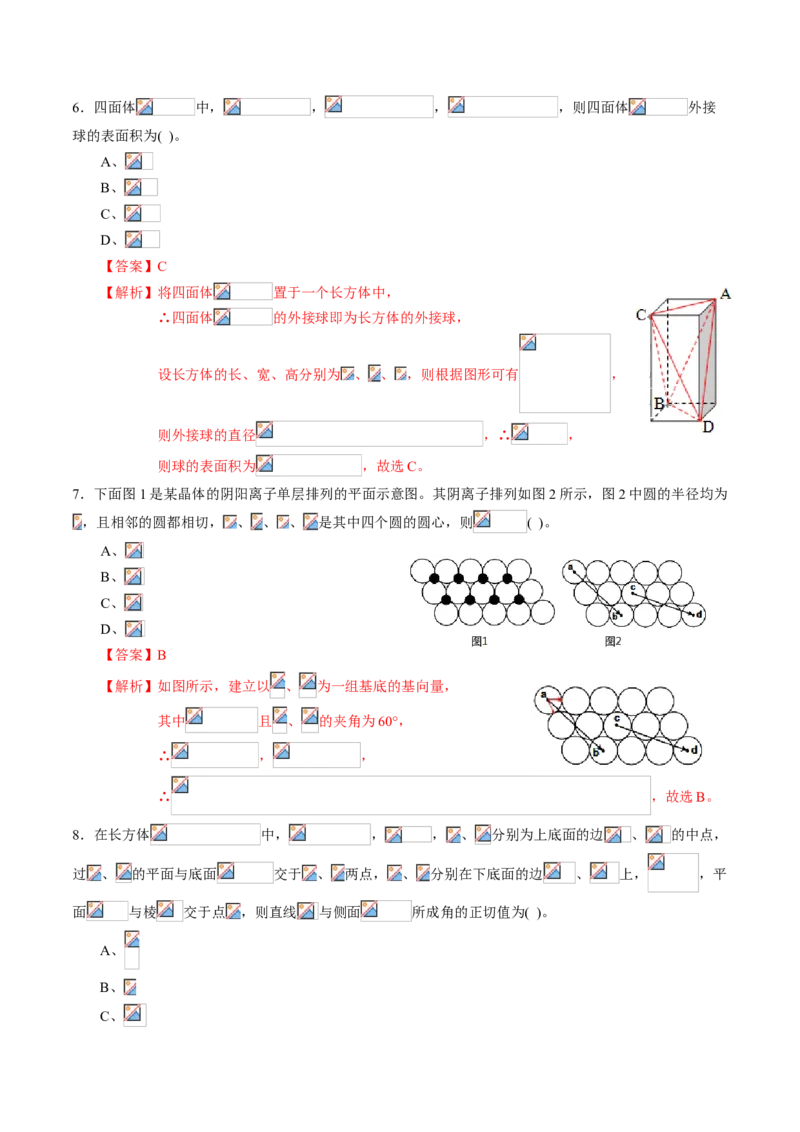
7.下面图1是某晶体的阴阳离子单层排列的平面示意图。其阴离子排列如图2所示,图2中圆的半径均为
,且相邻的圆都相切, 、 、 、 是其中四个圆的圆心,则 ( )。
A、
B、
C、
D、
【答案】B
【解析】如图所示,建立以 、 为一组基底的基向量,
其中 且 、 的夹角为60°,
∴ , ,
∴ ,故选B。
8.在长方体 中, , , 、 分别为上底面的边 、 的中点,
过 、 的平面与底面 交于 、 两点, 、 分别在下底面的边 、 上, ,平
面 与棱 交于点 ,则直线 与侧面 所成角的正切值为( )。
A、
B、
C、D、
【答案】A
【解析】延长 和 交于点 ,连接 ,
∵ 平面 ,平面 平面 ,
∴ ,且 ,
∵ ,∴ ,
∴ ,∴ ,又 ,∴ ,
∵ ∽ ,∴ ,且 ,∴ ,
∵ ∽ ,∴ ,且 ,
∴ ,又 ,∴ ,
又直线 与侧面 所成角为 ,则 ,故选A。
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,
全部选对的得5分,部分选对的得3分,有选错的得0分.
9.设 为虚数单位,则下列命题错误的是( )。
A、 ,复数 是纯虚数
B、在复平面内 对应的点位于第三象限
C、若复数 ,则存在复数 ,使得
D、 ,方程 无解
【答案】ABD
【解析】A选项,只有当 时,复数 是纯虚数,错,
B选项, ,对应的点位于第一象限,错,
C选项,若复数 ,则存在复数 ,使得 ,对,
D选项, ,方程 成立,错,
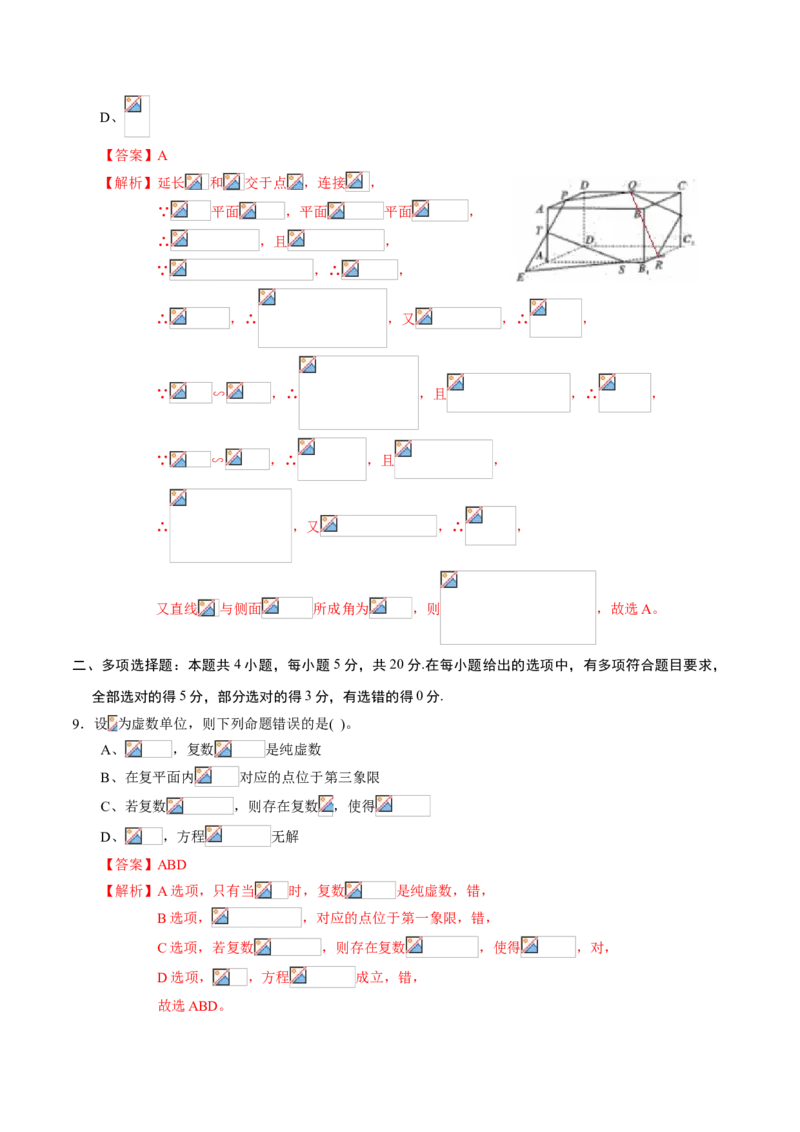
故选ABD。10.如图所示,在正方体 中, 、 分别是 、 的中点,则图中阴影部分在正方
体的六个面上的正投影(投射线垂直于投射面所得的平行投影)可能为下图中的( )。
A、 B、
C、 D、
【答案】AC
【解析】A选项为在 上的投影,C选项为在 上的投影。
11.设 、 、 是任意的非零平面向量,且相互不共线,则下列命题是真命题的有( )。
A、
B、
C、 不与 垂直
D、
【答案】BD
【解析】A选项,平面向量的数量积不满足结合律,故A假,
B选项,由向量的减法运算可知 、 、 恰为一个三角形的三条边长,
由“两边之差小于第三边”,故B真,
C选项,∵ ,
∴ 与 垂直,故C假,
D选项, ,成立,故D真,
故选BD。
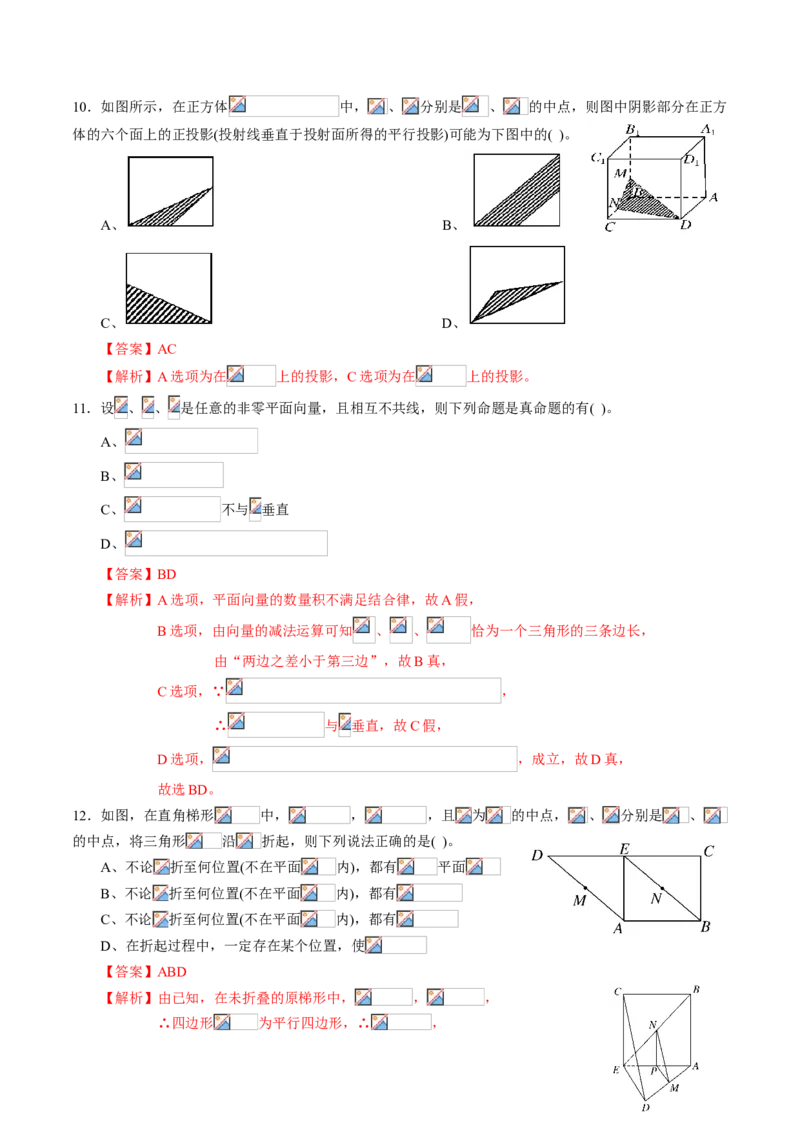
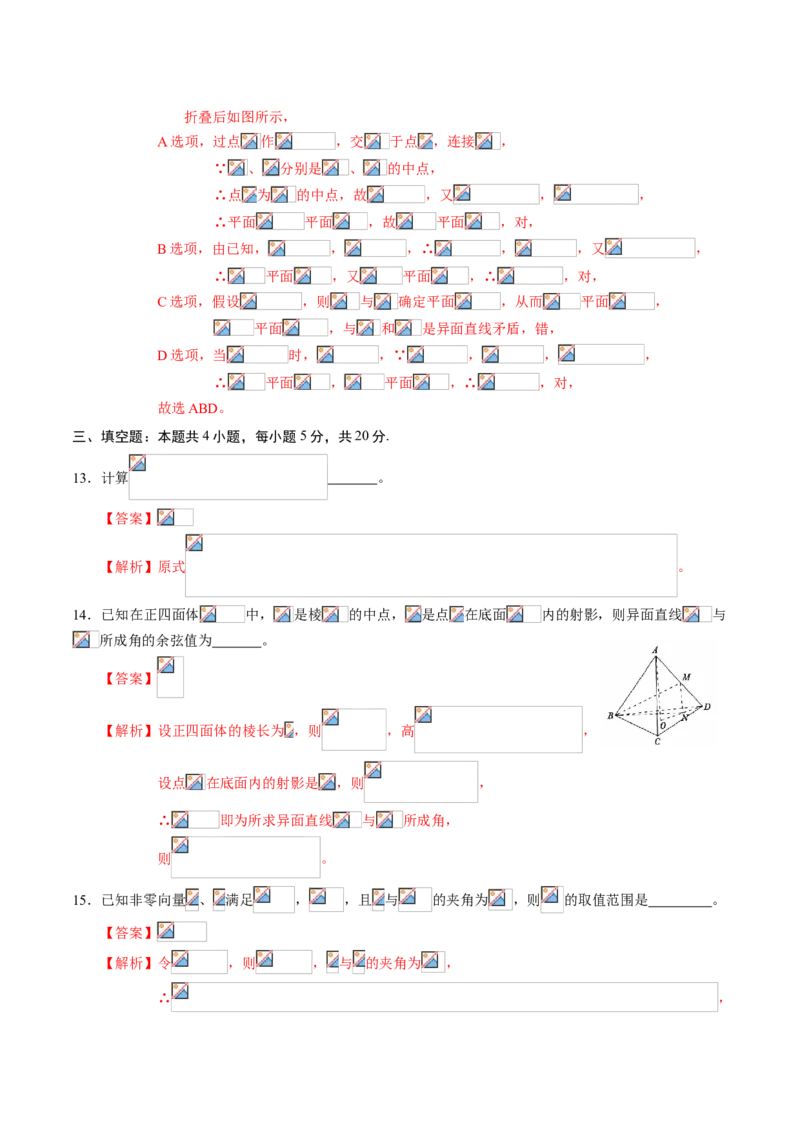
12.如图,在直角梯形 中, , ,且 为 的中点, 、 分别是 、
的中点,将三角形 沿 折起,则下列说法正确的是( )。
A、不论 折至何位置(不在平面 内),都有 平面
B、不论 折至何位置(不在平面 内),都有
C、不论 折至何位置(不在平面 内),都有
D、在折起过程中,一定存在某个位置,使
【答案】ABD
【解析】由已知,在未折叠的原梯形中, , ,
∴四边形 为平行四边形,∴ ,折叠后如图所示,
A选项,过点 作 ,交 于点 ,连接 ,
∵ 、 分别是 、 的中点,
∴点 为 的中点,故 ,又 , ,
∴平面 平面 ,故 平面 ,对,
B选项,由已知, , ,∴ , ,又 ,
∴ 平面 ,又 平面 ,∴ ,对,
C选项,假设 ,则 与 确定平面 ,从而 平面 ,
平面 ,与 和 是异面直线矛盾,错,
D选项,当 时, ,∵ , , ,
∴ 平面 , 平面 ,∴ ,对,
故选ABD。
三、填空题:本题共4小题,每小题5分,共20分.
13.计算 。
【答案】
【解析】原式 。
14.已知在正四面体 中, 是棱 的中点, 是点 在底面 内的射影,则异面直线 与
所成角的余弦值为 。
【答案】
【解析】设正四面体的棱长为 ,则 ,高 ,
设点 在底面内的射影是 ,则 ,
∴ 即为所求异面直线 与 所成角,
则 。
15.已知非零向量 、 满足 , ,且 与 的夹角为 ,则 的取值范围是 。
【答案】
【解析】令 ,则 , 与 的夹角为 ,
∴ ,又 ,∴ ,∴ 的取值范围是 。
16.如图所示,一竖立在地面上的圆锥形物体的母线长为 ,一只小虫从圆锥的底面圆上的点 出发,绕
圆锥爬行一周后回到点 处,若该小虫爬行的最短路程为 ,则这个圆锥的体积为 。
【答案】
【解析】作出该圆锥的侧面展开图,如图所示:
该小虫爬行的最短路程为 ,
由余弦定理可得 ,
∴ ,设底面圆的半径为 ,则有 ,
解得 ,∴这个圆锥的高为 ,
这个圆锥的体积为 。
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
已知 、 ,对于任意 ,均有 成立,试求实数 的取值范围。
【解析】∵ ,∴ , 2
分
∴ 对 恒成立, 4分
当 ,即 时,不等式恒成立, 6
分
当 时, , 9分
综上, 。 10分
18.(本小题满分12分)
已知三个点 , , 。
(1)求证: ;
(2)若四边形 为矩形,求点 的坐标以及矩形 两对角线所夹锐角的余弦值。
【解析】(1)证明:∵ , , ,∴ , , 2分
∵ ,∴ ,即 ; 4分
(2)解:∵ ,四边形 为矩形,∴ , 5分
设 点坐标为 ,则 , 6分
∴ ,解得 ,∴点 坐标为 , 7
分
从而 , ,
且 , , , 9
分
设 与 的夹角为 ,则 , 11
分
∴矩形 的两条对角线所夹锐角的余弦值为 。 12
分
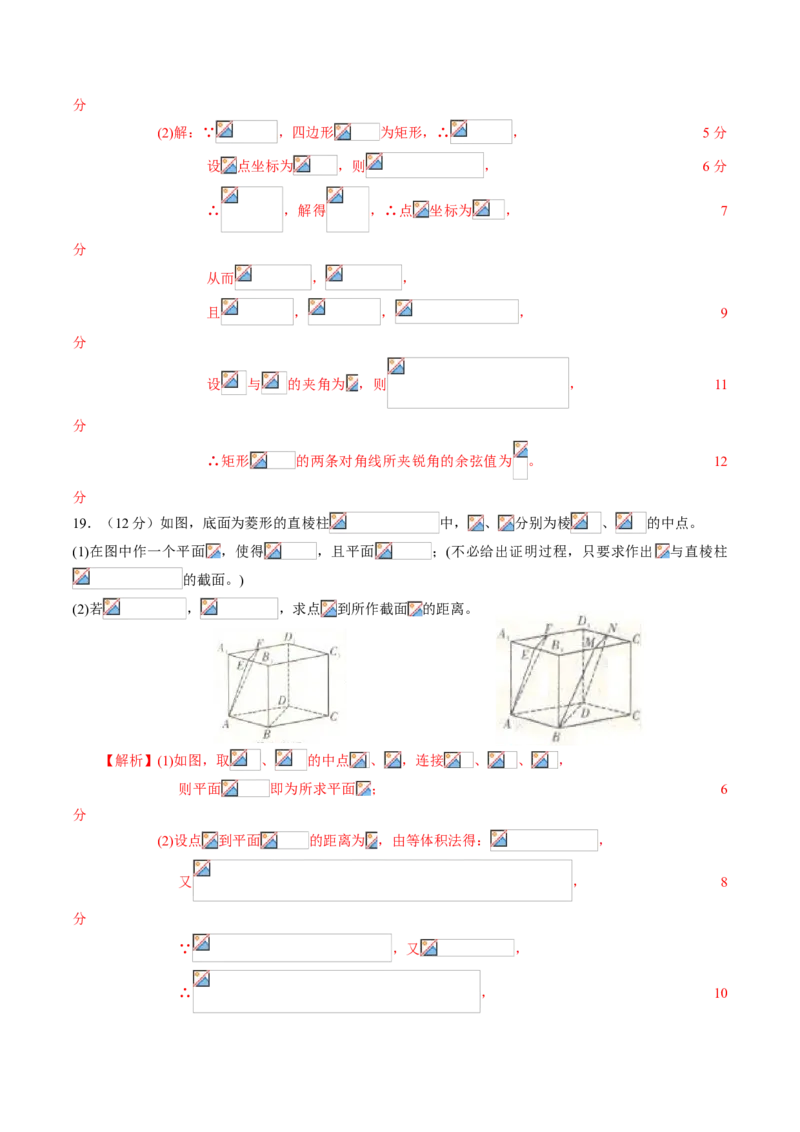
19.(12分)如图,底面为菱形的直棱柱 中, 、 分别为棱 、 的中点。
(1)在图中作一个平面 ,使得 ,且平面 ;(不必给出证明过程,只要求作出 与直棱柱
的截面。)
(2)若 , ,求点 到所作截面 的距离。
【解析】(1)如图,取 、 的中点 、 ,连接 、 、 ,
则平面 即为所求平面 ; 6
分
(2)设点 到平面 的距离为 ,由等体积法得: ,
又 , 8
分
∵ ,又 ,
∴ , 10分
又由 得: ,∴ 。 12分
20.(本小题满分12分)
如图,在以 、 、 、 、 、 为顶点的五面体中,平面 平面 , ,
,四边形 为平行四边形,且 。
(1)求证: ;
(2)若 , , ,求此五面体的体积。
【解析】(1)过 作 交 于 ,连接 ,
由平面 平面 ,平面 平面 ,
得 平面 ,∴ , 2
分
∵ , , ,∴ ≌ ,∴ ,
由已知 得 为等腰直角三角形,∴ , 4分
又 , , 平面 ,
∴ 平面 , ; 6分
(2)取 中点 ,连接 、 ,由(1)可知, ,又 ,
∴四边形 为平行四边形,棱柱 为斜棱柱且 为此斜棱柱的直截面,
在四棱锥 中,由(1)知, ,
又平面 平面 ,∴ 平面 ,
∴
。 12
分
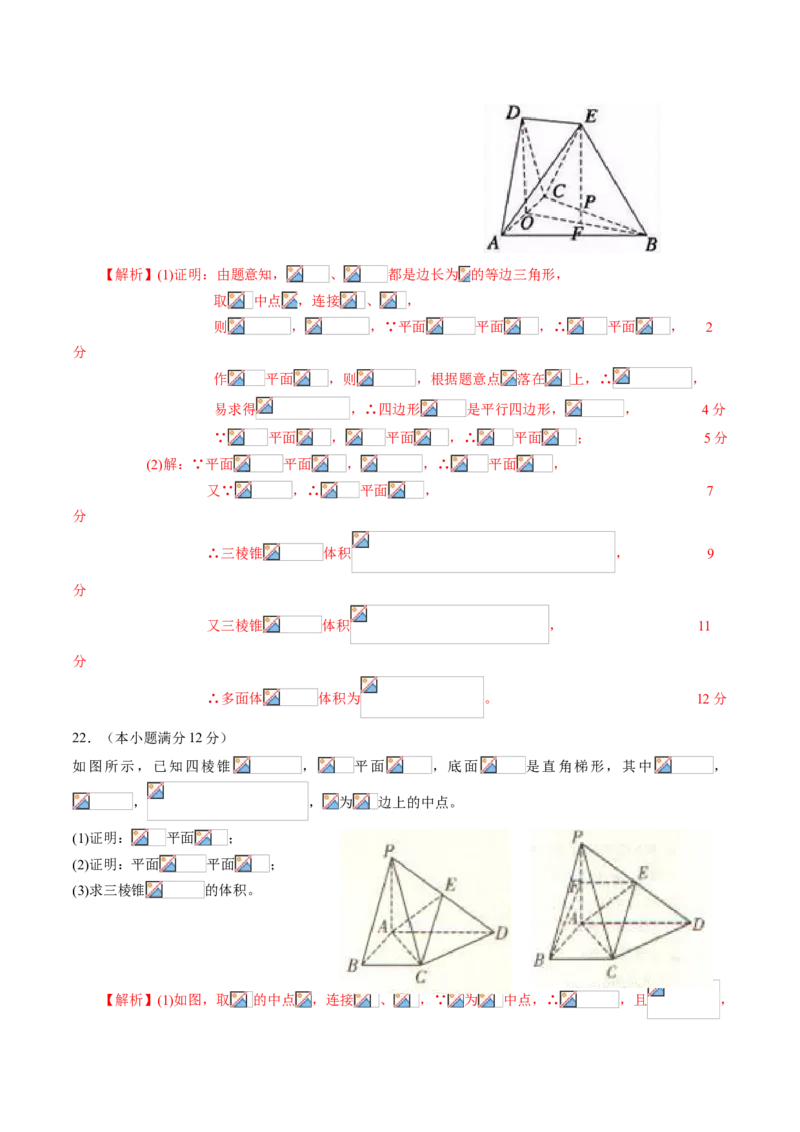
21.(本小题满分12分)
如图所示的空间几何体中,平面 平面 , , 和平面
所成的角为 ,且点 在平面 上的射影落在 的平分线上。
(1)求证: 平面 ;
(2)求多面体 的体积。【解析】(1)证明:由题意知, 、 都是边长为 的等边三角形,
取 中点 ,连接 、 ,
则 , ,∵平面 平面 ,∴ 平面 , 2
分
作 平面 ,则 ,根据题意点 落在 上,∴ ,
易求得 ,∴四边形 是平行四边形, , 4分
∵ 平面 , 平面 ,∴ 平面 ; 5分
(2)解:∵平面 平面 , ,∴ 平面 ,
又∵ ,∴ 平面 , 7
分
∴三棱锥 体积 , 9
分
又三棱锥 体积 , 11
分
∴多面体 体积为 。 12分
22.(本小题满分12分)
如图所示,已知四棱锥 , 平面 ,底面 是直角梯形,其中 ,
, , 为 边上的中点。
(1)证明: 平面 ;
(2)证明:平面 平面 ;
(3)求三棱锥 的体积。
【解析】(1)如图,取 的中点 ,连接 、 ,∵ 为 中点,∴ ,且 ,∵ , ,∴ 且 ,
∴四边形 是平行四边形, 2分
∴ ,又 平面 , 平面 ,∴ 平面 ; 4分
(2)在直角梯形 中, ,∴ ,
∴ ,即 , 6分
又 平面 ,∴ ,又 ,∴ 平面 ,
∵ 平面 ,∴平面 平面 ; 8
分
(3)∵ 为 边上的中点, 平面 ,
∴ , 10
分
∵ , ,∴ 。 12
分