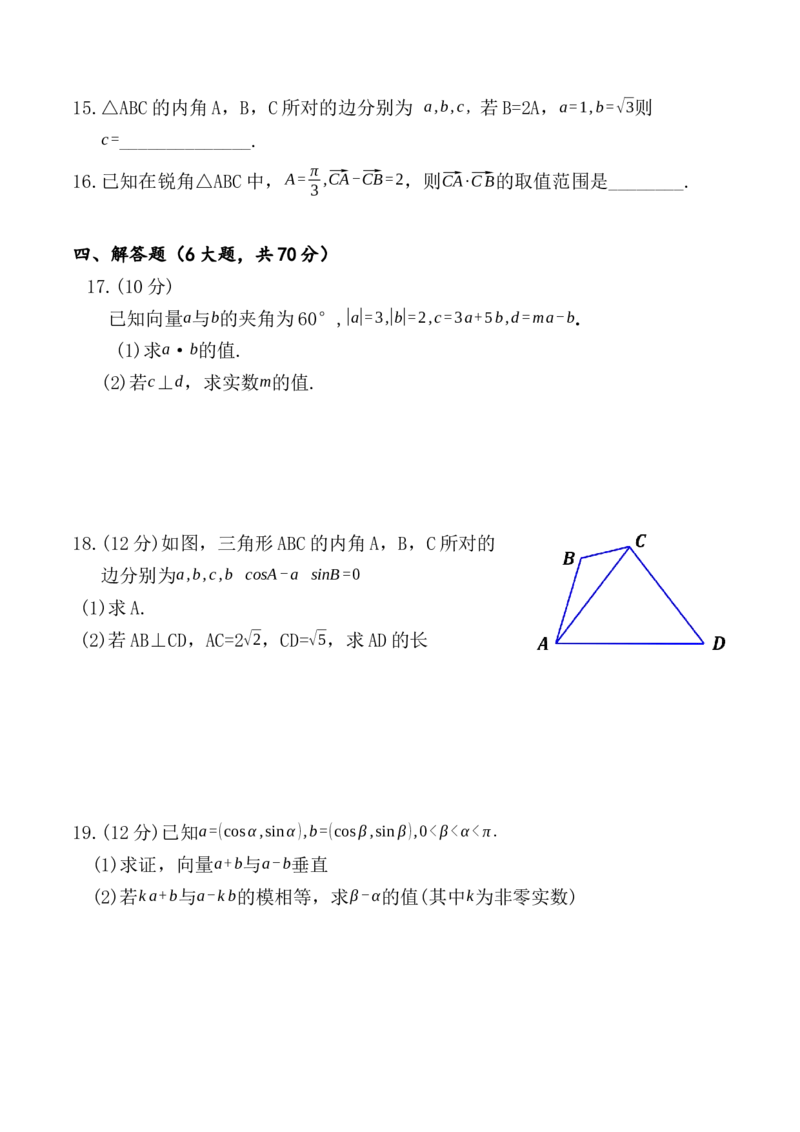文档内容
第二册 期中测试卷 02
高一数学
满分:150分 时间:120分钟
一、单项选择题(5分×8题=40分)
1.已知⃗AB=(5,-3),C=(-1,3),⃗CD=2⃗AB,则点D的坐标是( )
A.(11,-3) B. (9,-3) C. (9,3) D. (4,0)
π
2.已知向量a=(1,√3),b=(3,m),若向量a,b的夹角为 ,则m=( )
6
A.2√3 B. √3 C.0 D.-√3
3.设△ABC中BC边上的中线为AD,点O满足⃗AO=-2⃗DO,则⃗OC=( )
1 2 2 1 1 2 2 1
A.- ⃗AB+ ⃗AC B. ⃗AB- ⃗AO C. ⃗AB- ⃗AC D. - ⃗AB+ ⃗AC
3 3 3 3 3 3 3 3
4.已知向量a=(-2,1),b=(2,4), c=(-4,2),则下列结论正确的是( )
A. a//b,a//c B. a//b,a⊥c
C. a//b,b//c D. a⊥b,a//c
5.设△ABC 的内角 A,B,C 所对的边分别为a,b,c,若b cosC+c cosB+a sinA,则
△ABC的形状为( )
A.锐角三角形 B.直角三角形 C. 钝角三角形 D. 不确定
6.已知非零向量a,b满足:a=(1,1),|b|=1,(a-b)⊥b,则向量a,b的夹角大小为(
)
π π π π
A. B. C. D.
6 4 3 2
7.在△ABC 中,AC=2,BC=2√2,∠ACB=135°,过点 C 作 CD⊥AB 交 AB 于点 D,
则CD=( )
2√5
A. B.√2 C. √3 D. √5
5
√3 c b
8.在△ABC 中,角 A,B,C 所对的边分别为a,b,c,且 BC 边上的高为 a,则 +
6 b c
的最大值是( )
A. 8 B. 6 C. 3√2 D. 4
二、多项选择题(5 分×4 题=20 分,全选对 5 分,部分对 3 分,有错选不得分)
9.设a,b,c是任意的非零向量,则下列结论不正确的是( )
A. 0·a=0 B. (a·b)·c=a·(b·c)
C. a·b=0⇒a⊥b D. (a+b)·(a-b)=|a|2-|b|2
10.下列说法正确的有( )
A.在△ABC中,a:b:c=sinA:sinB:sinC
B.在△ABC中,若sin2A=sin2B,则a=b
C.在△ABC中,若sinA>sinB,则A>B,若A>B,则sinA>sinB都成立
a b+c
D.在△ABC中, =
sinA sinB+sinC
11. 设a,b是两个非零向量,则下列描述正确的有( )
A.若|a|+|b|=|a|-|b|,则存在实数λ,使得a=λb
B.若a⊥b,则|a|+|b|=|a|-|b|
C. 若|a+b|=|a|+|b| ,则a在b方向上的投影为a
D. 若存在实数λ,使得a=λb,则|a|+|b|=|a|-|b|
12.如图,设三角形ABC的内角A,B,C所对的边分别为
π
a,b,c,且√3(a cosC+c cosA)=2bsinB,且∠CAB= .
3
若点D是△ABC外一点,DC=1,DA=3,则下列说法中正
确的命题是( )
π
A.△ABC的内角B=
3
π
B.△ABC的内角C=
3
5√3
C.四边形ABCD面积的最大值为 +3
2
D.四边形ABCD面积无最大值
三、填空题(5分×4题=20分)
13.在△ABC中,若a=2,b=2√3,A=30°,则B=_________.
14.已知|a|=5,b=(2,1),且a//b,则向量a的坐标是________.15.△ABC的内角A,B,C所对的边分别为 a,b,c, 若B=2A,a=1,b=√3则
c=______________.
π
16.已知在锐角△ABC中,A= ,⃗CA-⃗CB=2,则⃗CA·⃗CB的取值范围是________.
3
四、解答题(6大题,共70分)
17.(10分)
已知向量a与b的夹角为60°,|a|=3,|b|=2,c=3a+5b,d=ma-b.
(1)求a·b的值.
(2)若c⊥d,求实数m的值.
18.(12分)如图,三角形ABC的内角A,B,C所对的
边分别为a,b,c,b cosA-a sinB=0
(1)求A.
(2)若AB⊥CD,AC=2√2,CD=√5,求AD的长
19.(12分)已知a=(cosα,sinα),b=(cosβ,sinβ),0<β<α<π.
(1)求证,向量a+b与a-b垂直
(2)若ka+b与a-kb的模相等,求β-α的值(其中k为非零实数)20.(12分)设三角形ABC的内角A,B,C所对的边分别为a,b,c,且
7
a+c=6,b=2,cosB=
9
(1)求a,c的值.
(2)求sin(A-B)的值.
21.(12分) 设三角形ABC的内角A,B,C所对的边分别为a,b,c,
且b sinB+c sinC=a sinA+c sinB.
(1)求角A的大小.
4√3
(2)若cosB= ,a=7√3,求△ABC的面积S的值.
7
22.(12分)已知向量a=(m,cos2x),b=(sin2x,n),函数f (x)=a·b,且
π 2π
y=f(x)的图像过点( ,√3)和点( ,-2).
12 3
(1)求m,n的值.
(2)将y=f(x)的图像向左平移φ(0<φ<π)个单位长度,得到函数y=g(x)的图像,
若y=f(x)的图像上各最高点到点(0,3)的距离的最小值为1,求
y=f(x)的单调递增区间.