文档内容
选择性必修第二册 期末模块检测试卷 基础A卷
学校:___________姓名:___________班级:___________考号:___________
题型:8(单选)+4(多选)+4(填空)+6(解答),满分150分,时间:120分钟
一、单选题
1.已知等比数列 中, , ,则 ( )
A. B. C. D.
2.已知等差数列 的前n项和为 , =5,则 =( )
A.5 B.25 C.35 D.50
3.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日五尺,问日织几何?”意
思是:“女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这名女子每天分
别织布多少?”某数学兴趣小组依托某制造厂用织布机完全模拟上述情景,则从第一天开始,要使织
布机织布的总尺数为165尺,则所需的天数为( )
A.7 B.8 C.9 D.10
4.观察下列式子: , , ,…,则可归纳出
小于( )
A. B. C. D.
5.设曲线 在点 处的切线方程为 ,则 ( )
A.0 B.1 C.2 D.3
6.已知数列 , 都是等差数列,记 , 分别为 , 的前n项和,且
,则 =( )A. B. C. D.
7.已知函数 ,其导函数为 ,则
的值为( )
A.1 B.2 C.3 D.4
8.已知函数 有两个零点,则实数 的取值范围是( )
A. B. C. D.
二、多选题
9.已知递减的等差数列 的前 项和为 , ,则( )
A. B. 最大
C. D.
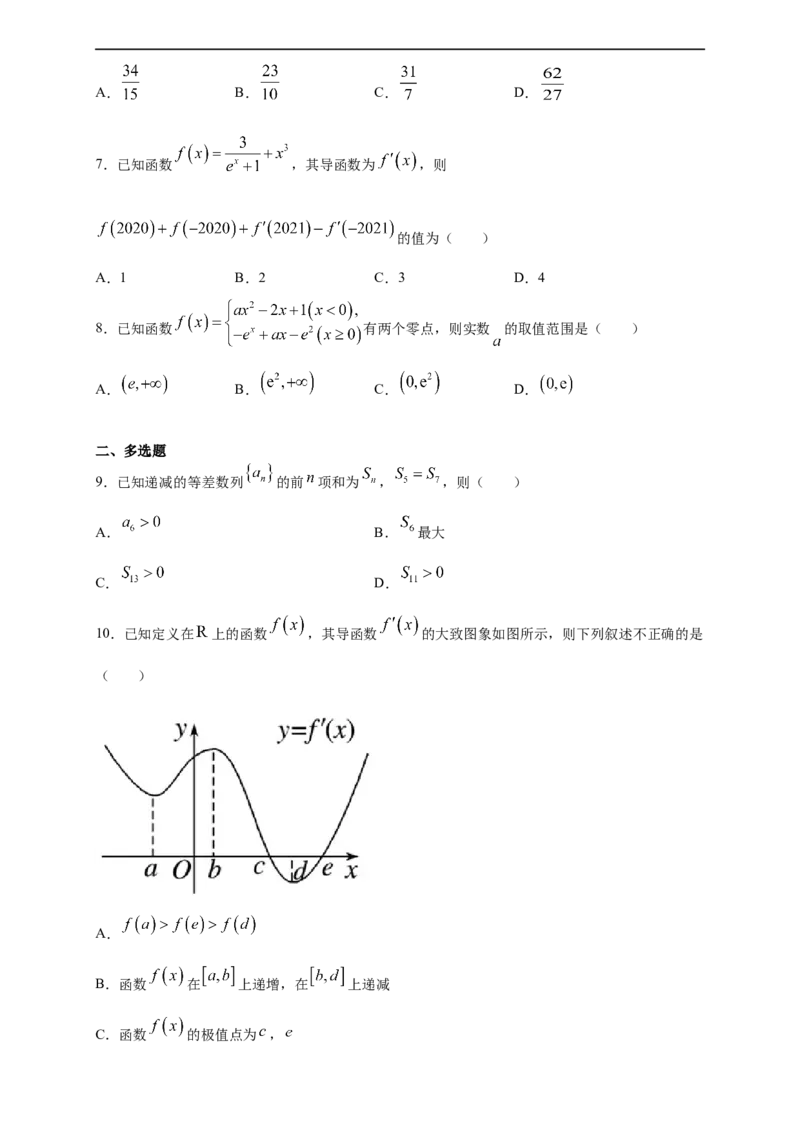
10.已知定义在 上的函数 ,其导函数 的大致图象如图所示,则下列叙述不正确的是
( )
A.
B.函数 在 上递增,在 上递减
C.函数 的极值点为 ,D.函数 的极大值为
11.在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一
半,如此六日过其关”.则下列说法正确的是( )
A.此人第六天只走了5里路
B.此人第一天走的路程比后五天走的路程多6 里
C.此人第二天走的路程比全程的 还多1.5里
D.此人走的前三天路程之和是后三天路程之和的8倍
12.已知数列 的前 项和为 ,则下列说法正确的是( )
A. B. 为 的最小值
C. D.
三、填空题
13.已知 ,则 等于__________.(用数字作答)
14. 对任意 都有 .数列 满足:
,则 __________.
15.已知 ,对任意的 都有 ,则 的取值范围为_______.
16.古代埃及数学中有一个独特现象:除 用一个单独的符号表示以外,其他分数都可写成若干个
单分数和的形式.例如 ,可这样理解:假定有两个面包,要平均分给5个人,如果每人
,不够,每人 ,余 ,再将这 分2成5份,每人得 ,这样每人分得 .形如的分数的分解: , , ,按此规律,则
________ .
四、解答题
17.已知数列 各项均为正数,其前 项和为 ,且满足 .
(1)求数列 的通项公式.
(2)设 ,求数列 的前 项和 .
18.在① ,② ,③ 这三个条件中任选两个,补充在下面的问题
中.若问题中的 存在,求出 的值;若不存在,请说明理由.
设等差数列 的前 项和为 , 是各项均为正数的等比数列,设前 项和为 ,若
, ,且 .是否存在大于 的正整数 ,使得 成等比数列?
(注:如果选择多个条件分别解答,按第一个解答计分.)
19.已知数列 中, ,
(1)证明:数列 是等比数列
(2)若数列 满足 ,求数列 的前 项和 .
20.已知函数
(1)求函数 的单调区间;
(2)若方程 =0有两个不相等的实数根,求实数 的取值范围.21.设函数 , .
(1) 时,求 的最小值.
(2)若 在 恒成立,求 的取值范围.
22.已知 .
(1)若函数 在 处取得极值,求实数 的值;
(2)若 ,求函数 的单调递增区间;
(3)若 ,存在正实数 ,使得 成立,求 的取值范围.