1999年湖南高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_湖南

1999 年湖南高考理科数学真题及答案 第I卷（选择题 共60分） 注意事项： l．答第I卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型（A或B） 用铅笔涂写在答题卡上。 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡 皮擦干净后。再选涂其它答案，不能答在试题卷上。 3．考试结束。监考人将本试卷和答题卡一并收回。 参考公式： 三角函数的积化和差公式 1 1 sincos sin()sin() cossin sin()sin() 2 2 1 coscos cos()cos() 2 正棱台、圆台的侧面积公式： 1 S  (cc)l 其中c、c分别表示上、下底面周长，l表示斜高或母线长． 台侧 2 4 球的体积公式：V  r3，其中R表示球的半径． 球 3 1 台体的体积公式：V  （S‘  S'S S)h，其中S'，S 分别表示上下底面积，h 台体 3 表示高。 一、选择题：本大题共14小题；第1—10题每小题4分，第11—14题每小题5分，共60 分在每小题给出的四个选顶中，只有一顶是符合题目要求的。 （1）如图,I是全集,M、P、S、是I的3个子集，由阴影部分所表示的集合是 ( ) （A）(M N) S （B）(M P)S （C）(M P)S （D）(M P)S （2）已知映射f:A  B,其中，集合A{3,2,1,1,2,3,},集合B中的元素都是A中 第1页 | 共11页元素在映射f下的象，且对任意的a A ,在B中和它对应的元素是{a},则集合B中元 素的个数是 ( ) （A）4 （B）5 （C）6 （D）7 （3）若函数y=f(x)的反函数是y=g(x),f(a)=b,ab 0,则g(b)等于 ( ) （A）a （B）a1 （C）b （D）b1 （4）函数f(x)=Msin(x)(0)在区间[a,b]上是增函数，且f(a)=-M,f(b)=M,则函 数g(x)=Mcos(x)在[a,b]上 ( ) (A)是增函数 （B）是减函数 （C）可以取得最大值M （D）可以取得最小值－M （5）若f(x)sinx是周期为的奇函数，则f(x)可以是 （A）sinx (B)cosx (C)sin2x (D)cos2x  （6）在极坐标系中，曲线 4sin( )关于 ( ) 3  5 (A)直线 对称 （B）直线 轴对称 3 6  （C）点(2, )中心对称 （D）极点中心对称 3 （７）若干毫升水倒入底面半径为２cm的圆柱形器皿中，量得水面的高度为６cm，若将这 些水倒入轴截面是正三角形的倒圆锥形器皿中，则水面的高度是 （ ） (A)6 3cm （B）6cm （C）2 （D）3 （8）若(2x 3)4  a a xa x2 a x3 a x4,则（a a a )2 (a a )2 0 1 2 3 4 0 2 4 1 3 的值为 （ ） (A)1 (B)-1 (C)0 (D)2 (9)直线 3x y2 3 0截圆x2  y2  4得的劣弧所对的圆心角为 （ ）     （A） (B) (C) (D) 6 4 3 2 (10) 如图，在多面体ＡＢＣＤＥＦ中 , 已知面ＡＢＣＤ是边长为３的正方形ＥＦ∥ＡＢＥ 第2页 | 共11页3 Ｆ＝ ,EF 与面ＡＣ的距离为２，则该多面体的体积 （ ） 2 9 15 （A） (B)5 (C)6 (D) 2 2   （11）若sintgctg (   ),则（ ） 2 2       (A)( , ) (B) ( ,0) (C) (0, ) (D) ( , ) 2 4 4 4 4 2 （12）如果圆台的上底面半径为5，下底面半径为R，中截面把圆台分为上、下两个圆台， 它们的侧面积的比为1∶2，那么R＝（ ） （A）10 （B）15 （C）20 （D）25 5 5 （13）已知丙点M（1， )、N(4, ),给出下列曲线方程：4x+2y-1=0 ②x2  y2 3 4 4 x2 x2 ③  y2 1 ④  y2 1在曲线上存在点P满足 MP  NP 的所有曲线方程是 2 2 （A）①③ （B）②④ （C）①②③ （D）②③④ （14）某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和 盒装磁盘。根据需要，软件至少买3片，磁盘至少买2盒，则不同的选购方式共有（ ） （A）5种 （B）6种 （C）7种 （D）8种 二、填空题：本大题共4小题；每小题4分，共16分。把答案填在题中横线上。 x2 y2 （15）设椭圆  （1 a b 0)的右焦点为F，右准线为L .若过F 且垂直于x a2 b2 1 2 1 轴的弦的长等于点F 到L 的距离，则椭圆的离心率是 。 1 1 （16）在一块并排10 垄的田地中，选择2垄分别种植A、B两种作物，每种作物种植一垄， 为有利于作物生长，要求A、B两种作物的间隔不小于6垄，则不同的选垄方法共有_____种 (用数字作答） （17）若正数a、b满足ab=a+b+3,则ab的取值范围是 （18）、是两个不同的平面，m、n是平面、之外的两条直线。给出四个论断： 第3页 | 共11页① mn ②  ③ n ④m以其中三个论断作为条件，余下一个论断作为结 论，写出你认为正确的一个命题： 三．解答题：本大题共6小题；共74分。解答应写出文字说明、证明过程或演算步骤。 （19）（本小题满分10） 解不等式 3log x2  2log x1 (a.0,a 1) a a （20）（本小题满分12分）  设复数z＝3cosi2sin.求函数y argz (0 )的最大值以及对应的值 2 (21)(本小题满分12分) 如 图 ： 已 知 正 四 棱 锥 ABCD － A BC D ,点E在棱D D上，截面EAC∥ 1 1 1 1 1 D B,且面EAC与底面ABCD所成的角为45， 1 AB＝a （1）求截面EAC的面积； （2）求异面直线A B与AC之间的距离； 1 1 （3）求三棱锥B－EAC的体积。 1 第4页 | 共11页（22）（本小题满分12分） 右图为一台冷轧机的示意图。冷 轧机由若干对轧辊组成，带钢从一端 输入，经过各对轧辊 逐步减薄后输出。 （1）输入钢带的厚度为,输出钢带的厚度为， 若每对轧辊的减薄率不超过r ，问冷轧机至少需要 0 安装多少对轧辊？ 输入该对的带钢厚度－从该对输出的带钢厚度 （一对轧辊减薄率＝ ） 输入该对的带钢厚度 （2）已知一台冷轧机共有4台减薄率为20％的轧辊，所有轧辊周长均为1600mm。若第k 对轧辊有缺陷，每滚动一周在带钢上压出一个疵点，在冷轧机输出的带钢上，疵点 的间距为l .为了便于检修，请计算L .L L 并填入下表（轧钢过程中，带钢宽度 k 1 2 3 不变，且不考虑损耗） 轧钢序列号k 1 2 3 4 疵点间距L （单位mm） 1600 k (23)(本小题满分14分) 已知函数y=f(x)的图象是自原点出发的一条折线。当 第5页 | 共11页n  y  n1(n 0,1,2)时，该图象是斜率为bn的线段（其中正常数b 1）， 设数列{x }由f(x )  n(n 1,2,)定义。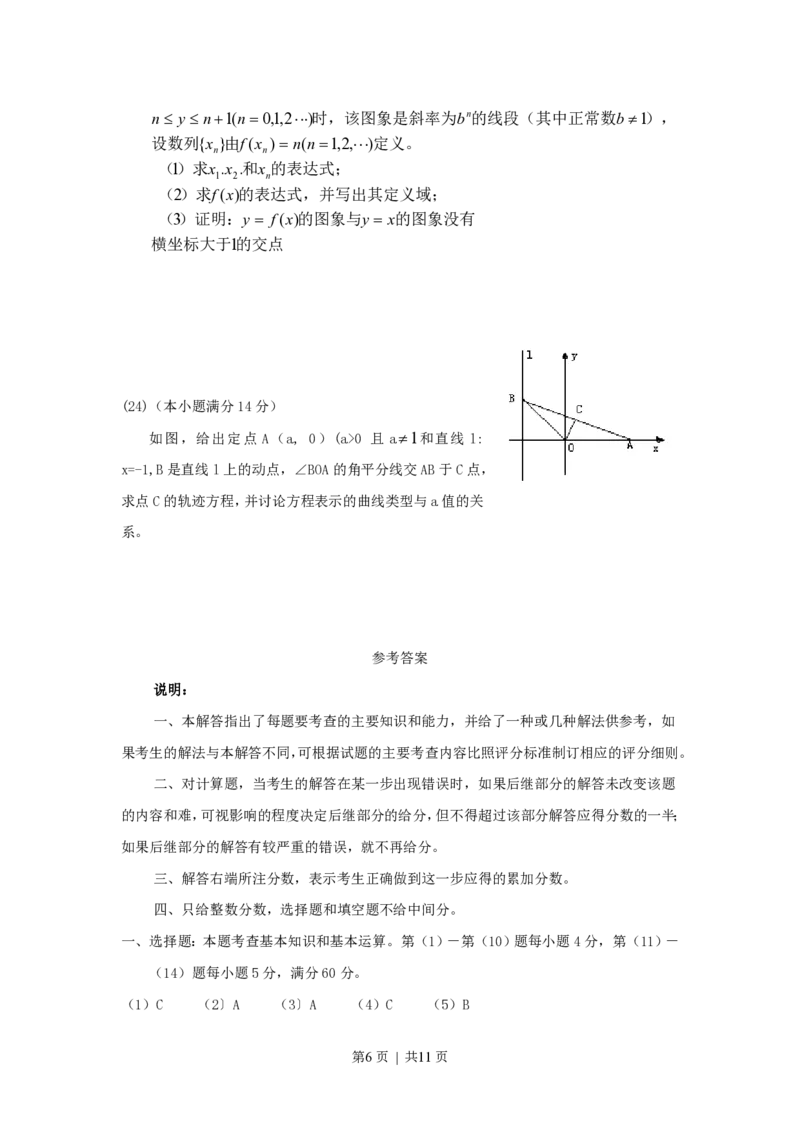 n n （1）求x .x .和x 的表达式； 1 2 n （2）求f(x)的表达式，并写出其定义域； （3）证明：y  f(x)的图象与y  x的图象没有 横坐标大于1的交点 (24)（本小题满分14分） 如图，给出定点 A（a, 0）(a>0 且 a1和直线 l: x=-1 ,B是直线l上的动点，∠BOA的角平分线交AB于C点， 求点C的轨迹方程，并讨论方程表示的曲线类型与a值的关 系。 参考答案 说明： 一、本解答指出了每题要考查的主要知识和能力，并给了一种或几种解法供参考，如 果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则。 二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题 的内容和难，可视影响的程度决定后继部分的给分，但不得超过该部分解答应得分数的一半； 如果后继部分的解答有较严重的错误，就不再给分。 三、解答右端所注分数，表示考生正确做到这一步应得的累加分数。 四、只给整数分数，选择题和填空题不给中间分。 一、选择题：本题考查基本知识和基本运算。第（1）－第（10）题每小题4分，第（11）－ （14）题每小题5分，满分60分。 （1）C （2〕A （3〕A （4）C （5）B 第6页 | 共11页（6）B （7）B （8）A （9）C （10）D （11）B （12）D （13）D （14）C 二、填空题：本题考查基本知识和基本运算，每小题4分，满分16分 1 （15） （16）12 （17）[9, +) 2 (18)m ,n, mn; 或mn,m,n 三． （19）本小题主要考查对数函数的性质，对数不等式、无理不等式解法等基础知识，考查分 类论的思想，满分10分 解：原不等式等价于   3 log x  2  0  a  3 log a x  2  (2 log a x 1) 2 可解得：  2 log x 1 0 a 2 3 当a>1时得所求的解集是：{xa3  x  a4}{xx  a} 3 2 当0＜a＜1时得所求的解集是：{xa4  x  a3}{x0 x  a} (20) 本小题主要考查复数的基本概念、三角公式和不等式等基础知识，考查综合运用所学 数学知识解决问题的能力，满分12分。  由0< 得tg0 2  2sin 2 由z=3cosi2sin,得0argz  及tg(argz)   tg 2 3cos 3 2 tg tg 3 1 故tgy=tg(argz)   2 2 1 tg2 2tg 3 tg 3 1 6 ∵ 2tg≥2 6 ∴ ≤ tg 3 12 2tg tg 3  6 当且仅当  2tg(0 )时,即tg 时,上式取等号 tg 2 2 第7页 | 共11页6 6 故当 arctg 时,函数tgy取最大值 2 12   ∵ y arctgz故y( , ). 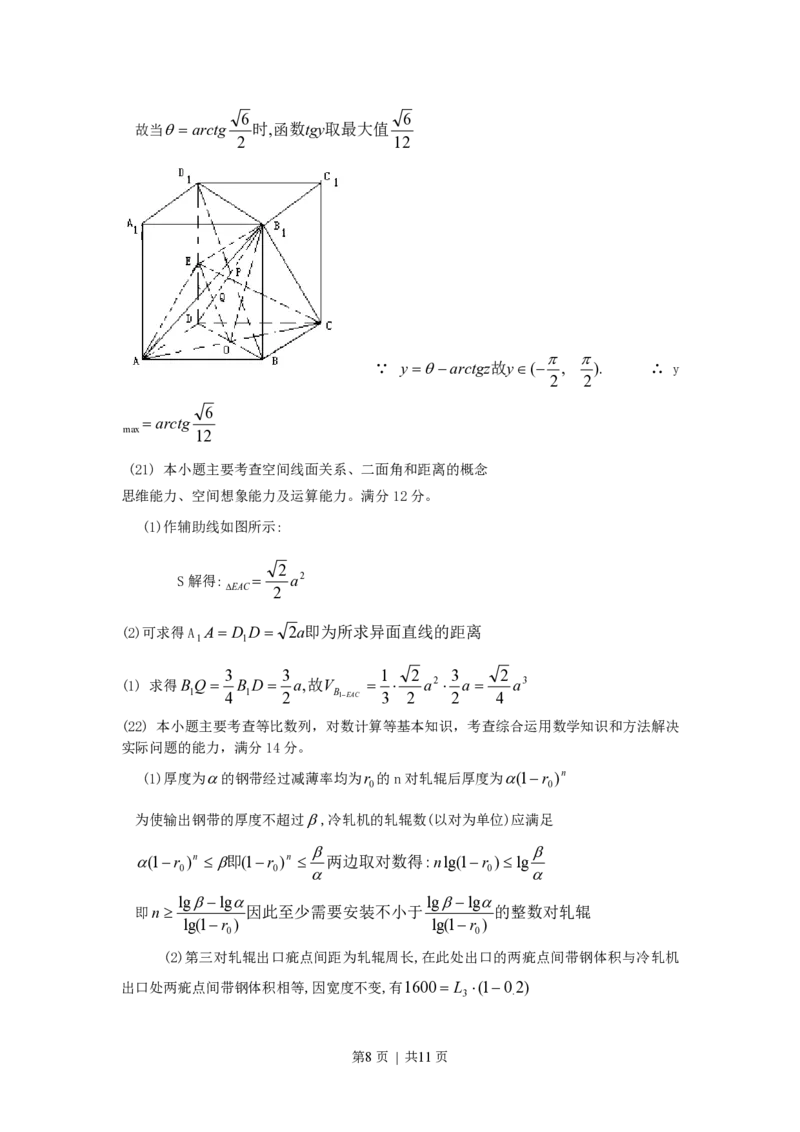∴ y 2 2 6  arctg max 12 (21) 本小题主要考查空间线面关系、二面角和距离的概念 思维能力、空间想象能力及运算能力。满分12分。 (1)作辅助线如图所示: 2 S解得:  a2 EAC 2 (2)可求得A A D D  2a即为所求异面直线的距离 1 1 3 3 1 2 3 2 (1) 求得BQ  B D  a,故V   a2  a  a3 1 4 1 2 B 1EAC 3 2 2 4 (22) 本小题主要考查等比数列，对数计算等基本知识，考查综合运用数学知识和方法解决 实际问题的能力，满分14分。 (1)厚度为的钢带经过减薄率均为r 的n对轧辊后厚度为(1r )n 0 0 为使输出钢带的厚度不超过,冷轧机的轧辊数(以对为单位)应满足   (1r )n 即(1r )n  两边取对数得:nlg(1r )lg 0 0  0  lglg lglg 即n 因此至少需要安装不小于 的整数对轧辊 lg(1r ) lg(1r ) 0 0 (2)第三对轧辊出口疵点间距为轧辊周长,在此处出口的两疵点间带钢体积与冷轧机 出口处两疵点间带钢体积相等,因宽度不变,有1600  L (10 2) 3  第8页 | 共11页1600 L L 故 L   2000(mm)同理 L  3  2500(mm) L  2 3125(mm) 3 08 2 08 2 08 填表如下: 轧钢序列号k 1 2 3 4 3125 2500 2000 1600 疵点间距L （单位mm） k (23) 本小题主要考查函数的基本概念、等比数列、数列极限的基础知识，考查归纳、推理 和综合的能力。满分14分。 (1)依题意 第9页 | 共11页(24) 本小题主要考查曲线与方程，直线和圆锥曲线等基础知识，以及求动点轨迹的基本 技能和综合运用数学知识解决问题的能力。满分14分。 依题意,记(-1, b) (bR),则直线OA和OB的方程分别为y=0和y=-bx.设点C(x,y),则有0  x  a,由OC平分∠AOB,知点C到OA.OB距离相等,根据点到直线的距离公式得 ybx y  ① 1b2 b 依题意设,点C在直线AB上,故有 y   (xa) 1a (1a)y 由xa  0b   ② xa 将②代入①得 (1a)2 y2 (1a)xy y2[1 ][y ]2  y [(1a)x2 2ax(1a)y2]0 (xa)2 xa 若y  0,则(1a)x2 2ax(1a)y2 0(0 x b) 若y=0,则b=0,∠AOB=,点C的坐标为(0, 0),满足上式. 综上得出点C的轨迹方程为 (1a)x2 2ax(1a)y2 0 (0 x  a) (ⅰ)当a=1时,轨迹方程化为y2  x (0 x  a) ③ 第10页 | 共11页a (x )2 1a y2 (ⅱ) 当a 1时,轨迹方程化为  1 (0 x  a) ④ a a2 ( )2 1a 1a2 所以,当01时,方程④表示双曲线一支的弧段. 第11页 | 共11页