文档内容
第二章 一元二次函数与不等式
本卷满分150分,考试时间120分钟。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一个选项是符合题目要求的.
1.已知关于 的不等式 的解集为R,则实数 的取值范围( )
A. B.
C. D.
【答案】B
【解析】当 时,不等式为 ,对 恒成立,所以满足条件
当 时,不等式为 ,解集为 ,不满足题意
当 时,对应的二次函数开口向上, 的解集一定不是R,
不满足题意
当 , 时,若不等式 的解集为R,则
,解得: ,综上,
故选:B
2.不等式 的解集是 ,则 的解集是( )
A. B. C. D.
【答案】C
【解析】:因为不等式 的解集是 ,
所以方程 的两根为 ,
所以由韦达定理得 , ,即 ,
所以 ,解不等式得解集为
故选:C
3.已知关于 的不等式 在 上有解,则实数 的取值范围是( )
A. B. C. D.
【答案】A【解析】由题意得, , ,即 ,
故问题转化为 在 上有解,
设 ,则 , ,
对于 ,当且仅当 时取等号,
则 ,
故 ,
故选:A
4.若实数 , ,满足 ,以下选项中正确的有( )
A. 的最小值为 B. 的最小值为
C. 的最小值为 D. 的最小值为
【答案】D
【解析】 实数 , , ,
整理得 ,当且仅当 时取 ,故选项A错误;
( ,
当且仅当 时取 ,故选项B错误;
, ,
,当且仅当 时取 ,
但已知 ,故不等式中的等号取不到,
,故选项C错误;
2,
,
,当且仅当 时取 ,故选项D正确,
故选:D
5.设 ,给出下列四个结论:① ;② ;③ ;④ .其
中正确的结论的序号为( )
A.①② B.①④ C.②③④ D.①②③
【答案】B
【解析】
【分析】因为 ,故 ,故①正确;
不妨取 ,满足 ,但 ,故②错误;
由 ,可得 ,故③错误;
由于 ,则 ,而 ,
故 ,即 ,故④正确,
故选:B
6.已知 , , ,则下列结论正确的是( )
A. 的最大值为9 B. 的最小值为
C. 的最小值为 D. 的最小值为
【答案】D
【解析】对于A,因为 ,所以
,
当且仅当 ,即 时,等号成立,即 的最小值为9,故A错误;
对于B, ,
当 时(此时 ) 取得最小值 ,故B错误;
对于C,因为 ,所以 ,当且仅当 时等号成立,所以 ,即 的最大值为 ,故C错误;
对于D, ,当且仅当 时等号成立,
所以 的最小值为 ,故D正确.
故选:D.
7.已知函数 ,设 ,若关于 的不等式 在 上
恒成立,则 的取值范围是( )
A. B. C. D.
【答案】B
【解析】不等式 可化为 (*).
当 时,(*)式即 .
即 .
又 (当 时取等号)
(当 时取等号).
所以 ,
当 时,(*)式为 , .
又 (当 时取等号),
(当 时取等号),所以 .
综上, .
故选:B.
8.已知函数 ,设关于 的不等式 的解集为 ,若
4,则实数a的取值范围是( )
A. B. C. D.
【答案】C
【解析】:显然当 时, ,不满足条件;
当 时,易知 ,当 时, ,于是 ,
而由 ,可得 ,即 ,所以 也不满足条件,
当 时,函数 ,
因为关于 的不等式 的解集为 ,若 ,则在 上,函数
的图象应在函数 的图象的下方,
如图所示,要使在 上,函数 的图象在函数 的图象的下方,
只要 即可,即 ,
化简可得 ,解得 ,
所以 的取值范围为 .
综上, 的取值范围为 .
故选:C.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项
符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知方程 及 分别各有两个整数根 , 及 , ,且
, 则下列结论一定正确的是( )
A. , , ,
B.
C.
D.
【答案】ACD
【解析】解:对于A:由 知, 与 同号.
若 ,则 ,这时 ,
所以 ,
此时与 矛盾,
所以 , .
同理可证 , 故A正确;
对于B:根据题意可知,
, , ,解得 .
同理 , ,
即 ,故B不正确,D正确;
对于C:由A知, , , , 是整数,所以 , .
由韦达定理有 ,
所以 ,故C正确;
故选:ACD.
10.已知关于x的不等式 的解集为 则( )
A.
B.不等式 的解集为
C.
D.不等式 的解集为
【答案】BC
6【解析】因为关于x的不等式 的解集为
所以 , 是方程 ,
所以A错误, ,则 ,
对于B,由 ,得 ,因为 ,所以 ,所以不等式 的解
集为 ,所以B正确,
对于C,因为 , ,所以 ,所以C正确,
对于D,不等式 可化为 ,因为 ,所以 ,
解得 ,所以原不等式的解集为 ,所以D错误,
故选:BC
11.下列说法正确的是( )
A.不等式 的解集为
B.若实数a,b,c满足 ,则
C.若 ,则函数 的最小值为2
D.当 时,不等式 恒成立,则k的取值范围是
【答案】AB对A,由 解得 或 ,所以A正确;
对B,由于 ,所以可以对 两边同除 ,得到 ,所以B正确;
对C,由于 ,所以 当且仅当 ,即
时取等号,显然不成立,所以C错误;
对D,①当 时,不等式为 ,恒成立;
②当 时,若要使不等式 恒成立,则 ,解得 ,
所以当 时,不等式 恒成立,则k的取值范围是 ,所以D错误.
故选:AB.
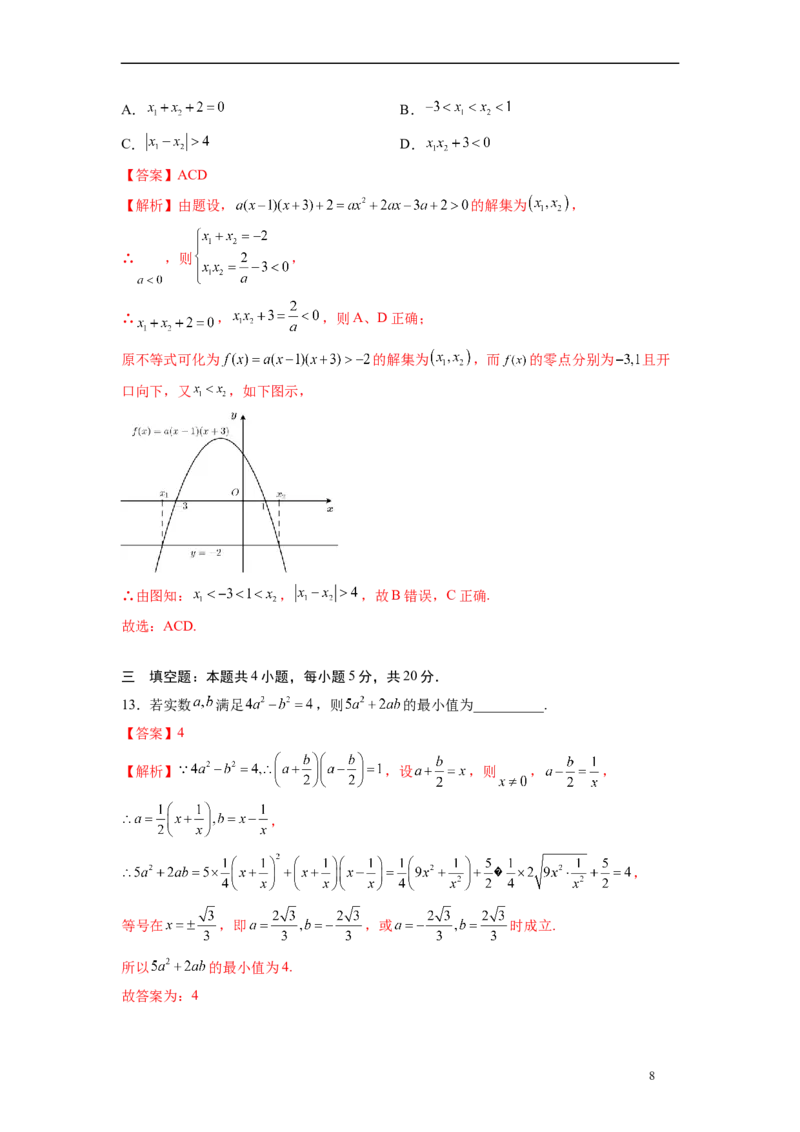
12.已知关于x的不等式 的解集是 ,其中 ,则下列结论中
正确的是( )A. B.
C. D.
【答案】ACD
【解析】由题设, 的解集为 ,
∴ ,则 ,
∴ , ,则A、D正确;
原不等式可化为 的解集为 ,而 的零点分别为 且开
口向下,又 ,如下图示,
∴由图知: , ,故B错误,C正确.
故选:ACD.
三 填空题:本题共4小题,每小题5分,共20分.
13.若实数 满足 ,则 的最小值为__________.
【答案】4
【解析】 ,设 ,则 , ,
,
,
等号在 ,即 ,或 时成立.
所以 的最小值为4.
故答案为:4
814.已知正实数a,b,满足 ,则 的最大值为___.
【答案】
【解析】:因为正实数 , ,满足 ,
则 ,
因为 , , ,
所以 ,当且仅当 时取等号,
令 , ,
则原式
,
当且仅当 ,即 时取等号,此时取得最大值 ,
故答案为: .
15.若对任意 , 恒成立,则 的最大值为
_________.
【答案】 ##
【解析】解:令 ,则 ,故 ,
对任意 , ,则 恒成立,
∴
∴ ,此时 ,
∴ ,当 时取等号,
此时 成立,
∴ 的最大值为 .
故答案为: .
16.已知关于x的方程 有4个不同的实数解,则实数a的取值范围是
___________.【答案】
【解析】由题意可知关于x的方程 有4个不同的实数解,可分为以下几种
情况:①当 时,方程 ,化为 ,解得 ,不满足题意,舍
掉;
②当 时,方程 ,化为 ,此方程有两个正根,即
,解得 ;
③当 时,方程 ,化为 ,此方程有两个负根,即
,解得 ;
由①②③可知,实数a的取值范围是 .
故答案为: .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17 (10分)
已知二次函数 ( 为实数)
(1)若 的解集为(1,2),求不等式 的解集;
(2)若对任意 , 时, 恒成立,求 的最小值;
(3)若对任意 , 恒成立,求ab的最大值.
【答案】(1) (2)1(3)
【解析】(1)依题意知, ,且方程 的两根为1,2由根与系数间的关
系得 ,则 .故不等式
解得: ,即原不等
式的解集为 .
(2)因为 时, 恒成立,故得 ,那 ,即
10,所以 (当且仅当 时等号成立)
(3)令 ,则 ,所以 .对任意 ,恒
成立,所以 恒成立.所以 且
所以 ,此时
,因此 ,当且仅当 时等号成立,此时
,(或 )验证,
成立故ab的最
大值为 .
18 (12分)
求实数 的范围,使关于 的方程
(1)有两个实根,且一个比 大,一个比 小;
(2)有两个实根 ,且满足 ;
(3)至少有一个正根.
【答案】(1) (2)
(3)
【解析】
(1)设 .
依题意有 ,即 ,得 .
(2)设 .
依题意有 ,解得 .
(3) .
方程至少有一个正根,则有三种可能:①有两个正根,此时可得 ,即
②有一个正根,一个负根,此时可得 ,得 .
③有一个正根,另一根为 ,此时可得
综上所述,得 .
19 (12分)已知关于 的一元二次函数
(1)若 的解集为 或 ,求实数 、 的值.
(2)若实数 、 满足 ,求关于 的不等式 的解集.
【答案】(1) (2)详见解析
(1) 的解集为 或 ,
与 是一元二次方程 的两个实数根,
,解得 .
(2) ,关于 的不等式 化为: ,
因式分解为: ,
当 时,化为 ,则 ;
当 时, ,解得 ,不等式的解集为 ;
时, ,解得 不等式的解集为 ;
时, ,不等式 化为: ,解得 或 ,不
等式的解集为 或 .
20(12分)
12已知函数 .
(1)当 时,求函数 在区间 上的值域;
(2)当 时,求函数 在区间 上的最大值;
(3)求 在 上的最大值与最小值.
【答案】(1) (2)
(3)答案见解析
(1)当 时, ,
函数在 上单调递减,在 上单调递增,
,
函数 在区间 上的值域是 ;
(2)当 时, ,
,函数 在区间 上的最大值 ;
,函数 在区间 上的最大值 ;
函数 在区间 上的最大值 ;
(3) 函数 的对称轴为 ,
①当 ,即 时,函数 在 上是增函数,
当 时,函数y取得最小值为 ;当 时,函数 取得最大值为 .
②当 ,即 时,
当 时,函数 取得最小值为 ;当 时,函数 取得最大值为 .
③当 ,即 时,
a时,函数 取得最小值为 ;当 时,函数 取得最大值为 .
④当 ,即 时,函数 在 上是减函数,
故当 时,函数 取得最大值为 ;当 时,函数 取得最小值为 .
综上,当 时,函数的最大值为 ,最小值为 ,当 时,函数的最
大值为 ,最小值为 ,当 时,函数的最大值为 ,最小值为,当 时,函数的最大值为 ,最小值为
21(12分)
某厂家拟进行某产品的促销活动,根据市场情况,该产品的月销售量a万件与月促销费用x
万元( )满足关系式 (k为常数),如果不搞促销活动,则该产品的月
销量是2万.已知生产该产品每月固定投入为8万元,每生产一万件该产品需要再投入5万
元,厂家将每件产品的销售价定为 元,设该产品的月利润为y万元.(注:利润=销
售收入-生产投入-促销费用)
(1)将y表示为x的函数;
(2)月促销费用为多少万元时,该产品的月利润最大?最大利润为多少?
【答案】(1) , .
(2)月促销费用为2万元时,该产品的月利润最大,最大为5万元.
【解析】(1)由题意知当 时, ,代入
则 ,解得 , .
利润 ,
又因为 ,
所以 , .
(2)由(1)知 ,
因为 时, ,
因为 ,当且仅当 时等号成立.
所以 ,
故月促销费用为2万元时,该产品的月利润最大,最大为5万元.
22(12分)
已知 是二次函数, 的解集是 ,且 在区间 上的最大值是12.
(1)求 的解析式;
14(2)解关于 的不等式 .
【答案】(1) (2)详见解析.
【解析】(1)解:因为 是二次函数,不等式 的解集是 ,
所以 ,
又 在区间 上的最大值是12,
所以 ,
解得 ,
所以 ;
(2)由(1)知不等式为 ,
即 ,
因为 ,即为 ,
当 时, ,所以 或 ,
当 时,则 ;
当 时, ,所以 或 ,
综上:当 时,不等式的解集为 ,
当 时,不等式的解集为 ;
当 时,不等式的解集是 .16