文档内容
福建省漳州市 2024-2025 学年高一上学期期末教学质量检测数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合𝐴={−1,0,1,2},𝐵 ={𝑥|𝑥2 ∈𝐴},则𝐴∩𝐵 =( )
A. {0,1} B. {−1,0,1} C. {0,1,2} D. {−1,0,1,2}
2.下列各组函数中,表示同一个函数的是( )
𝑥2−1
A. 𝑓(𝑥)=√ 𝑥2与𝑔(𝑥)=𝑥 B. 𝑓(𝑥)= 与𝑔(𝑥)=𝑥−1
𝑥+1
C. 𝑓(𝑥)=√ 𝑥3与𝑔(𝑥)=𝑥√ 𝑥 D. 𝑓(𝑥)=𝑥0与𝑔(𝑥)=1
3.已知角𝛼的顶点为坐标原点,始边与𝑥轴的非负半轴重合,点𝑃(−1,√ 2)在角𝛼的终边上,则sin(𝜋+𝛼)=( )
√ 6 √ 3 √ 3 √ 6
A. − B. − C. D.
3 3 3 3
4.已知关于𝑥的一元二次不等式𝑥2+𝑏𝑥+𝑐 >0的解集为{𝑥|𝑥 ≠−1},则𝑏𝑐 =( )
A. −2 B. −1 C. 1 D. 2
4 2
5.已知𝑎 =
3
,𝑏 =23,𝑐 =log
4
3,则( )
A. 𝑎 <𝑏 <𝑐 B. 𝑎 <𝑐 <𝑏 C. 𝑐 <𝑏 <𝑎 D. 𝑐 <𝑎 <𝑏
6.用二分法求函数𝑓(𝑥)=ln𝑥+𝑥−2在区间[1,2]上的零点近似解,要求精确度为0.01时,所需二分区间的
次数最少为( )
A. 5 B. 6 C. 7 D. 8
𝜋
7.某同学用“五点法”画函数𝑓(𝑥)=𝐴sin(𝜔𝑥+𝜑)(𝐴>0,𝜔 >0,|𝜑|< )在一个周期内的图象时,列表并
2
填入了部分数据,如下表:
𝜋 3𝜋
𝜔𝑥+𝜑 0 𝜋 2𝜋
2 2
2𝜋 13𝜋
𝑥
9 18
𝐴sin(𝜔𝑥+𝜑) 0 2
根据这些数据,要得到函数𝑦 =𝐴sin𝜔𝑥的图象,需要将函数𝑓(𝑥)的图象( )
𝜋 𝜋
A. 向左平移 个单位长度 B. 向右平移 个单位长度
18 18
𝜋 𝜋
C. 向左平移 个单位长度 D. 向右平移 个单位长度
6 6
1 1
8.用max{𝑎,𝑏}表示𝑎与𝑏的最大者,记𝑀 =max{4𝑥+ , +𝑦},其中𝑥,𝑦都是正数,则𝑀的最小值为( )
𝑦 𝑥
A. 2√ 2 B. 3 C. 8 D. 9
第1页,共8页二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
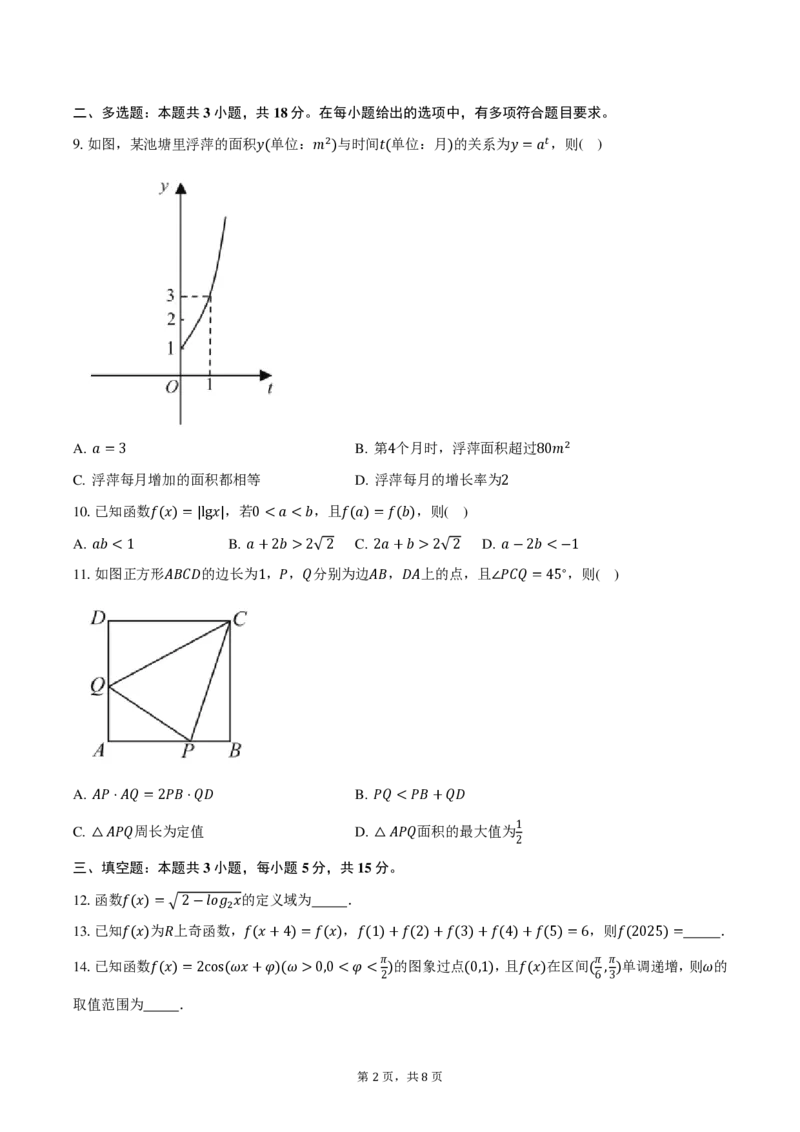
9.如图,某池塘里浮萍的面积𝑦(单位:𝑚2)与时间𝑡(单位:月)的关系为𝑦=𝑎𝑡,则( )
A. 𝑎 =3 B. 第4个月时,浮萍面积超过80𝑚2
C. 浮萍每月增加的面积都相等 D. 浮萍每月的增长率为2
10.已知函数𝑓(𝑥)=|lg𝑥|,若0<𝑎 <𝑏,且𝑓(𝑎)=𝑓(𝑏),则( )
A. 𝑎𝑏 <1 B. 𝑎+2𝑏 >2√ 2 C. 2𝑎+𝑏 >2√ 2 D. 𝑎−2𝑏 <−1
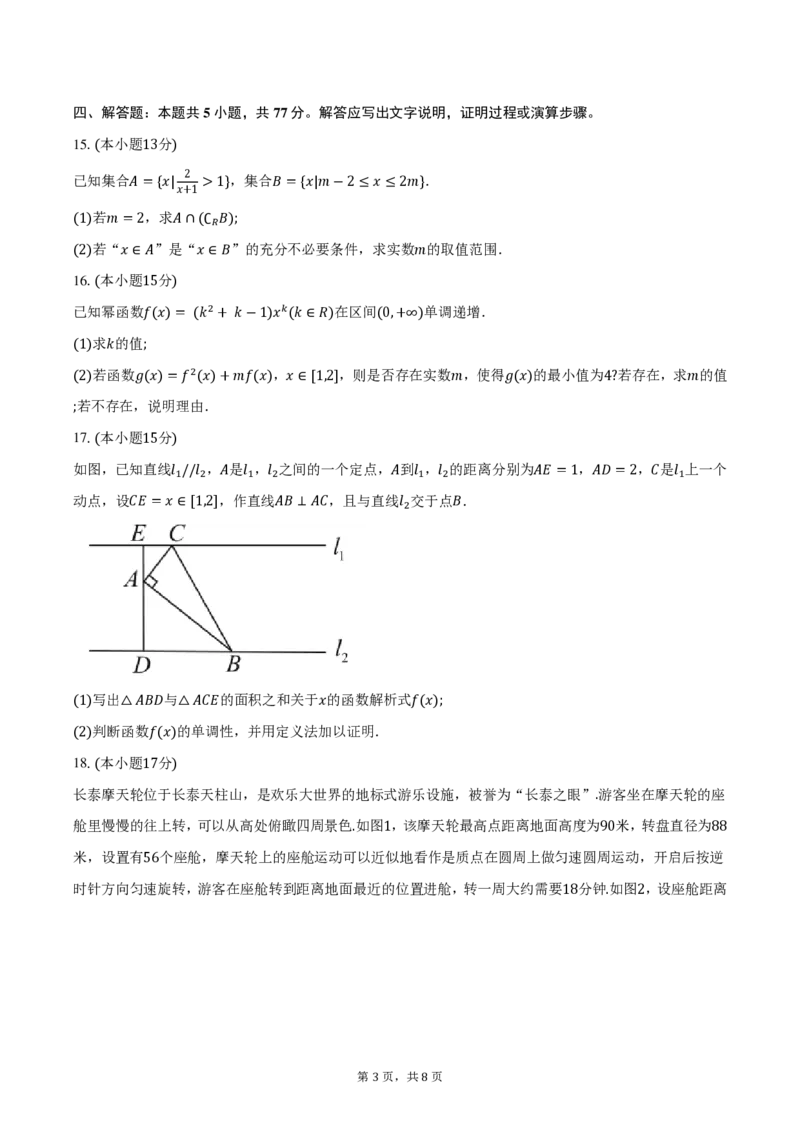
11.如图正方形𝐴𝐵𝐶𝐷的边长为1,𝑃,𝑄分别为边𝐴𝐵,𝐷𝐴上的点,且∠𝑃𝐶𝑄 =45∘,则( )
A. 𝐴𝑃⋅𝐴𝑄 =2𝑃𝐵⋅𝑄𝐷 B. 𝑃𝑄 <𝑃𝐵+𝑄𝐷
1
C. △𝐴𝑃𝑄周长为定值 D. △𝐴𝑃𝑄面积的最大值为
2
三、填空题:本题共3小题,每小题5分,共15分。
12.函数𝑓(𝑥)=√ 2−𝑙𝑜𝑔 𝑥的定义域为 .
2
13.已知𝑓(𝑥)为𝑅上奇函数,𝑓(𝑥+4)=𝑓(𝑥),𝑓(1)+𝑓(2)+𝑓(3)+𝑓(4)+𝑓(5)=6,则𝑓(2025)= .
𝜋 𝜋 𝜋
14.已知函数𝑓(𝑥)=2cos(𝜔𝑥+𝜑)(𝜔 >0,0<𝜑 < )的图象过点(0,1),且𝑓(𝑥)在区间( , )单调递增,则𝜔的
2 6 3
取值范围为 .
第2页,共8页四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
2
已知集合𝐴 ={𝑥| >1},集合𝐵 ={𝑥|𝑚−2≤𝑥 ≤2𝑚}.
𝑥+1
(1)若𝑚 =2,求𝐴∩(∁ 𝐵);
𝑅
(2)若“𝑥 ∈𝐴”是“𝑥 ∈𝐵”的充分不必要条件,求实数𝑚的取值范围.
16.(本小题15分)
已知幂函数𝑓(𝑥)= (𝑘2+ 𝑘−1)𝑥𝑘(𝑘 ∈𝑅)在区间(0,+∞)单调递增.
(1)求𝑘的值;
(2)若函数𝑔(𝑥)=𝑓2(𝑥)+𝑚𝑓(𝑥),𝑥 ∈[1,2],则是否存在实数𝑚,使得𝑔(𝑥)的最小值为4?若存在,求𝑚的值
;若不存在,说明理由.
17.(本小题15分)
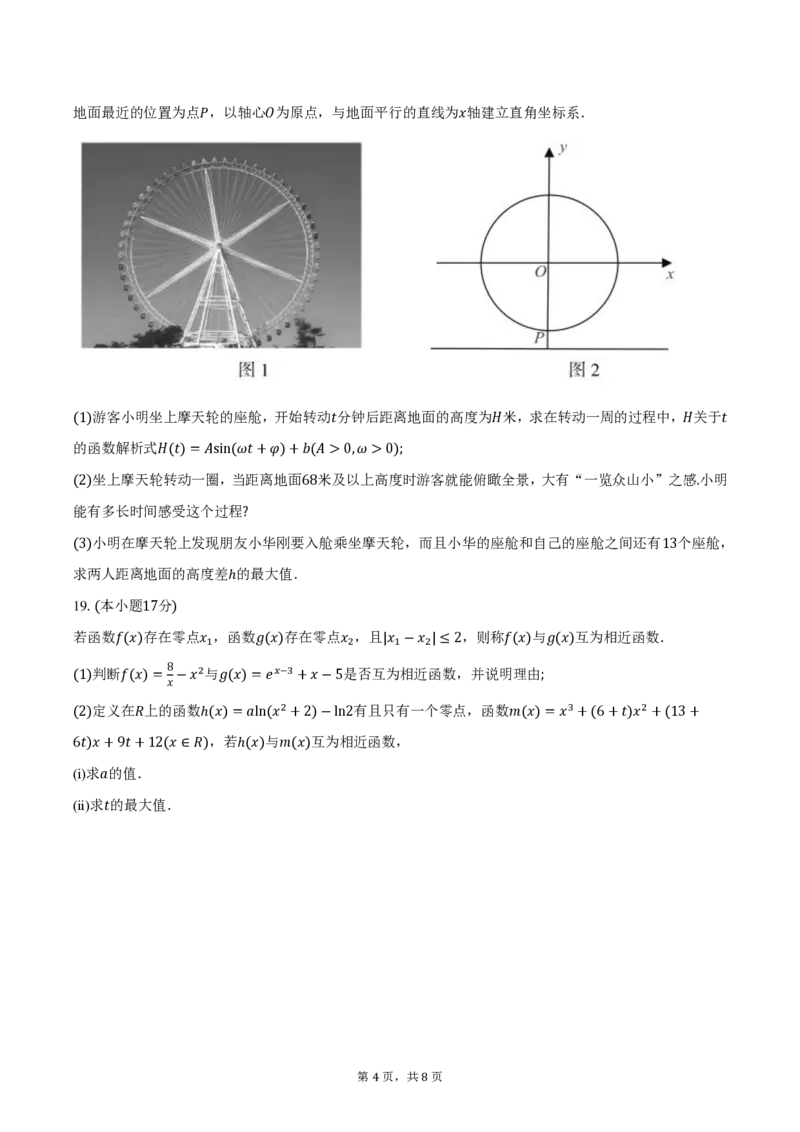
如图,已知直线𝑙 //𝑙 ,𝐴是𝑙 ,𝑙 之间的一个定点,𝐴到𝑙 ,𝑙 的距离分别为𝐴𝐸 =1,𝐴𝐷 =2,𝐶是𝑙 上一个
1 2 1 2 1 2 1
动点,设𝐶𝐸 =𝑥 ∈[1,2],作直线𝐴𝐵 ⊥𝐴𝐶,且与直线𝑙 交于点𝐵.
2
(1)写出△𝐴𝐵𝐷与△𝐴𝐶𝐸的面积之和关于𝑥的函数解析式𝑓(𝑥);
(2)判断函数𝑓(𝑥)的单调性,并用定义法加以证明.
18.(本小题17分)
长泰摩天轮位于长泰天柱山,是欢乐大世界的地标式游乐设施,被誉为“长泰之眼”.游客坐在摩天轮的座
舱里慢慢的往上转,可以从高处俯瞰四周景色.如图1,该摩天轮最高点距离地面高度为90米,转盘直径为88
米,设置有56个座舱,摩天轮上的座舱运动可以近似地看作是质点在圆周上做匀速圆周运动,开启后按逆
时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要18分钟.如图2,设座舱距离
第3页,共8页地面最近的位置为点𝑃,以轴心𝑂为原点,与地面平行的直线为𝑥轴建立直角坐标系.
(1)游客小明坐上摩天轮的座舱,开始转动𝑡分钟后距离地面的高度为𝐻米,求在转动一周的过程中,𝐻关于𝑡
的函数解析式𝐻(𝑡)=𝐴sin(𝜔𝑡+𝜑)+𝑏(𝐴>0,𝜔 >0);
(2)坐上摩天轮转动一圈,当距离地面68米及以上高度时游客就能俯瞰全景,大有“一览众山小”之感.小明
能有多长时间感受这个过程?
(3)小明在摩天轮上发现朋友小华刚要入舱乘坐摩天轮,而且小华的座舱和自己的座舱之间还有13个座舱,
求两人距离地面的高度差ℎ的最大值.
19.(本小题17分)
若函数𝑓(𝑥)存在零点𝑥 ,函数𝑔(𝑥)存在零点𝑥 ,且|𝑥 −𝑥 |≤2,则称𝑓(𝑥)与𝑔(𝑥)互为相近函数.
1 2 1 2
8
(1)判断𝑓(𝑥)= −𝑥2与𝑔(𝑥)=𝑒𝑥−3+𝑥−5是否互为相近函数,并说明理由;
𝑥
(2)定义在𝑅上的函数ℎ(𝑥)=𝑎ln(𝑥2+2)−ln2有且只有一个零点,函数𝑚(𝑥)=𝑥3+(6+𝑡)𝑥2+(13+
6𝑡)𝑥+9𝑡+12(𝑥 ∈𝑅),若ℎ(𝑥)与𝑚(𝑥)互为相近函数,
(ⅰ)求𝑎的值.
(ⅱ)求𝑡的最大值.
第4页,共8页1.【答案】𝐵
2.【答案】𝐶
3.【答案】𝐴
4.【答案】𝐷
5.【答案】𝐷
6.【答案】𝐶
7.【答案】𝐴
8.【答案】𝐵
9.【答案】𝐴𝐵𝐷
10.【答案】𝐵𝐷
11.【答案】𝐴𝐶
12.【答案】(0,4]
13.【答案】6
14.【答案】[4,5]
2 1−𝑥
15.【答案】解:(1)由 >1,得 >0,解得−1<𝑥 <1,
𝑥+1 𝑥+1
所以𝐴 ={𝑥|−1<𝑥 <1},
若𝑚 =2,𝐵 ={𝑥|0≤𝑥 ≤4},∁ 𝐵 ={𝑥|𝑥 <0或𝑥 >4}.
𝑅
所以𝐴∩(∁ 𝐵)={𝑥|−1<𝑥 <0}.
𝑅
(2)因为“𝑥 ∈𝐴”是“𝑥 ∈𝐵”的充分不必要条件,
𝑚−2≤−1
所以𝐴 ⫋𝐵,所以{ 且等号布同时取,,
2𝑚≥1
1 1
解得 ≤𝑚 ≤1,所以实数𝑚的取值范围为[ ,1].
2 2
16.【答案】解:(1)因为𝑓(𝑥)是幂函数,所以𝑘2+𝑘−1=1,
解得𝑘 =−2或𝑘 =1,
当𝑘 =−2时,𝑓(𝑥)=𝑥−2在区间(0,+∞)单调递减,不符合题意,
当𝑘 =1时,𝑓(𝑥)=𝑥在区间(0,+∞)单调递增,符合题意,
所以𝑘 =1
(2)由(1)函数𝑓(𝑥)的解析式为𝑓(𝑥)=𝑥,函数𝑔(𝑥)=𝑓2(𝑥)+𝑚𝑓(𝑥),
第5页,共8页𝑚
即𝑔(𝑥)=𝑥2+𝑚𝑥,𝑥 ∈[1,2],函数𝑦 =𝑥2+𝑚𝑥的对称轴为𝑥 =− ,
2
𝑚
①当− ≤1,即𝑚 ≥−2时,则𝑔(𝑥) =𝑔(1)=1+𝑚 =4,解得𝑚 =3,满足题意;
2 min
𝑚 𝑚 𝑚2
②当1<− <2时,即−4<𝑚 <−2,则𝑔(𝑥) =𝑔(− )=− =4,无解,舍去;
2 min 2 4
𝑚
③当− ≥2时,即𝑚 ≤−4时,则𝑔(𝑥) =𝑔(2)=4+2𝑚 =4,解得𝑚 =0,不满足,舍去;
2 min
综上所述,存在𝑚 =3使得𝑔(𝑥)的最小值为4.
𝜋 𝜋
17.【答案】解:(1)由已知,∠𝐴𝐵𝐷+∠𝐷𝐴𝐵 = ,∠𝐸𝐴𝐶+∠𝐷𝐴𝐵 = ,
2 2
所以∠𝐸𝐴𝐶 =∠𝐴𝐵𝐷,
𝜋
又因为∠𝐴𝐸𝐶 =∠𝐴𝐷𝐵 = ,所以𝛥𝐴𝐶𝐸 ∽△𝐵𝐴𝐷,
2
𝐶𝐸 𝐴𝐷 2
所以 = ,已知𝐴𝐸 =1,𝐴𝐷 =2,𝐶𝐸 =𝑥,得𝐵𝐷 = ,
𝐴𝐸 𝐵𝐷 𝑥
1 1 1 2 1 2 𝑥
所以𝑓(𝑥)= ×𝐴𝐷×𝐵𝐷+ ×𝐴𝐸×𝐸𝐶 = ×2× + ×1×𝑥 = + ,𝑥 ∈[1,2],
2 2 2 𝑥 2 𝑥 2
2 𝑥
函数𝑓(𝑥)的解析式为𝑓(𝑥)= + (𝑥 ∈[1,2]).
𝑥 2
(2)函数𝑓(𝑥)在𝑥 ∈[1,2]单调递减.
2 𝑥
证明如下:由(1)𝑓(𝑥)= + (𝑥 ∈[1,2])
𝑥 2
任取𝑥 ,𝑥 ∈[1,2],且𝑥 <𝑥 ,
1 2 1 2
2 𝑥 2 𝑥 (𝑥 −𝑥 )(𝑥 𝑥 −4)
则𝑓(𝑥 )−𝑓(𝑥 )= + 1−( + 2)= 1 2 1 2 ,
1 2 𝑥 2 𝑥 2 2𝑥 𝑥
1 2 1 2
(𝑥 −𝑥 )(𝑥 𝑥 −4)
因为1≤𝑥 <𝑥 ≤2,所以𝑥 −𝑥 <0,𝑥 𝑥 −4<0,𝑥 𝑥 >0,所以 1 2 1 2 >0,
1 2 1 2 1 2 1 2 2𝑥 𝑥
1 2
即𝑓(𝑥 )−𝑓(𝑥 )>0,𝑓(𝑥 )>𝑓(𝑥 ),
1 2 1 2
所以𝑓(𝑥)在𝑥 ∈[1,2]单调递减
18.【答案】解:(1)𝐻(𝑡)=𝐴sin(𝜔𝑡+𝜑)+𝑏(𝐴>0,𝜔 >0),
𝐴+𝑏 =90 𝐴=44
由题意知{ ,解得{ ,
−𝐴+𝑏 =90−88 𝑏 =46
2𝜋 𝜋
又𝑇 = =18,解得𝜔 = ,
𝜔 9
𝜋 𝜋
所以𝐻(𝑡)=44sin( 𝑡+𝜑)+46,因为𝐻(0)=2,所以sin𝜑 =−1,所以𝜑 =2𝑘𝜋− ,𝑘 ∈𝑍,所以𝐻(𝑡)=
9 2
𝜋 𝜋
44sin( 𝑡+2𝑘𝜋− )+46,𝑡 ∈[0,18];
9 2
𝜋 𝜋 𝜋 𝜋
(2)由(1) 𝐻(𝑡)=44sin( 𝑡+2𝑘𝜋− )+46=−44cos 𝑡+46.令𝐻(𝑡)=−44cos 𝑡+46≥68,
9 2 9 9
第6页,共8页𝜋 1 𝜋 1
则−cos 𝑡 ≥ ,即cos 𝑡 ≤− ,
9 2 9 2
𝜋 2𝜋 𝜋 4𝜋
因为𝑡 ∈[0,18],则 𝑡 ∈[0,2𝜋],所以 ≤ 𝑡 ≤ ,解得𝑡 ∈[6,12],
9 3 9 3
所以小明坐上摩天轮能有12−6=6(分钟)感受这个过程;
2𝜋 𝜋
(3)由题意知,两人间隔的弧度数为 ×14= ,
56 2
𝜋
所以小明经过𝑡分钟后距离地面的高度为𝐻 =−44cos 𝑡+46,
1 9
𝜋 𝜋
小华距离地面的高度为𝐻 =−44cos( 𝑡− )+46,𝑡 ∈[0,18];
2 9 2
𝜋 𝜋 𝜋
则两人离地高度差ℎ =|𝐻 −𝐻 |=|−44cos 𝑡+44cos( 𝑡− )|
1 2 9 9 2
𝜋 𝜋 𝜋 𝜋
|−44𝑐𝑜𝑠 𝑡+44𝑠𝑖𝑛 𝑡|=44√ 2|𝑠𝑖𝑛 ( 𝑡− )|⩽44√ 2,
9 9 9 4
𝜋 𝜋 𝜋 3𝜋 27 63
当 𝑡− = (或 ),即𝑡 = (或 )时,ℎ的最大值为44√ 2米.
9 4 2 2 4 4
8
19.【答案】(1)令𝑓(𝑥)= −𝑥2 =0,解得𝑥 =2,即𝑓(𝑥)有唯一零点2
𝑥
因为𝑔(𝑥)=𝑒𝑥−3+𝑥−5在𝑅上单调递增且连续,
而且𝑔(3)=−1<0,𝑔(4)=𝑒−1>0,𝑔(3)𝑔(4)<0,所以𝑔(𝑥)存在唯一零点𝑥 ,且𝑥 ∈(3,4),
0 0
8
所以满足|𝑥 −2|≤2,所以𝑓(𝑥)= −𝑥2与𝑔(𝑥)=𝑒𝑥−3+𝑥−5互为相近函数.
0 𝑥
(2) (𝑖)已知定义在𝑅上的函数ℎ(𝑥)=𝑎ln(𝑥2+2)−ln2,对𝑅上的任意一个𝑥,
都有ℎ(−𝑥)=𝑎ln[(−𝑥)2+2]−ln2= 𝑎ln(𝑥2+ 2)−ln2= ℎ(𝑥),所以ℎ(𝑥)为偶函数,
又已知ℎ(𝑥)有且只有一个零点,所以ℎ(0)=𝑎ln2−ln2=0,解得𝑎 =1;
经检验,当𝑎 =1时,ℎ(𝑥)有唯一零点0.
(𝑖𝑖)由(𝑖)知,ℎ(𝑥)有且只有一个零点为0,
又ℎ(𝑥)与𝑚(𝑥)=𝑥3+(6+𝑡)𝑥2+(13+6𝑡)𝑥+9𝑡+12互为相近函数,
所以𝑚(𝑥)=0在[−2,2]上有解,
由𝑚(𝑥)=0,
即𝑥3+(6+𝑡)𝑥2+(13+6𝑡)𝑥+9𝑡+12=0,
所以(𝑥+3)2⋅𝑡 =−(𝑥3+6𝑥2+13𝑥+12),
令𝑧 =𝑥+3,因为𝑥 ∈[−2,2],所以𝑧 ∈[1,5],
第7页,共8页𝑥3+6𝑥2+13𝑥+12 (𝑧−3) 3 +6(𝑧−3) 2 +13(𝑧−3)+12 𝑧3−3𝑧2+4𝑧
𝑡 =− =− =−
(𝑥+3)
2 𝑧2 𝑧2
4 4
=−(𝑧+ −3)⩽−(2√ 𝑧· −3)=−1
𝑧 𝑧
4
当且仅当𝑧 = ,𝑧 =2,即𝑥 =−1时,𝑡取到最大值为−1.
𝑧
第8页,共8页