文档内容
A级:“四基”巩固训练
一、选择题
1.下列不等式中一元二次不等式的个数为( )
①(m+1)x2>x ②-x2+5x+6>0
③(x+a)(x+a+1)<0 ④2x2-x>2
A.1 B.2 C.3 D.4
答案 C
解析 由一元二次不等式的定义可知,②③④为一元二次不等式.
2.若不等式x2-4x>2ax+a对一切实数x都成立,则实数a的取值范围是(
)
A.1-1 D.a<1或a>4
答案 B
解析 不等式x2-4x>2ax+a可变形为x2-(4+2a)x-a>0,∵该不等式对一
切实数x恒成立,∴Δ<0,即(4+2a)2-4·(-a)<0,化简得a2+5a+4<0,解得-
40的解集为{x|-30
的解集为( )
A.
B.
C.{x|-30,即(2x-1)(3x+1)>0,解得x<-或x>.故选B.
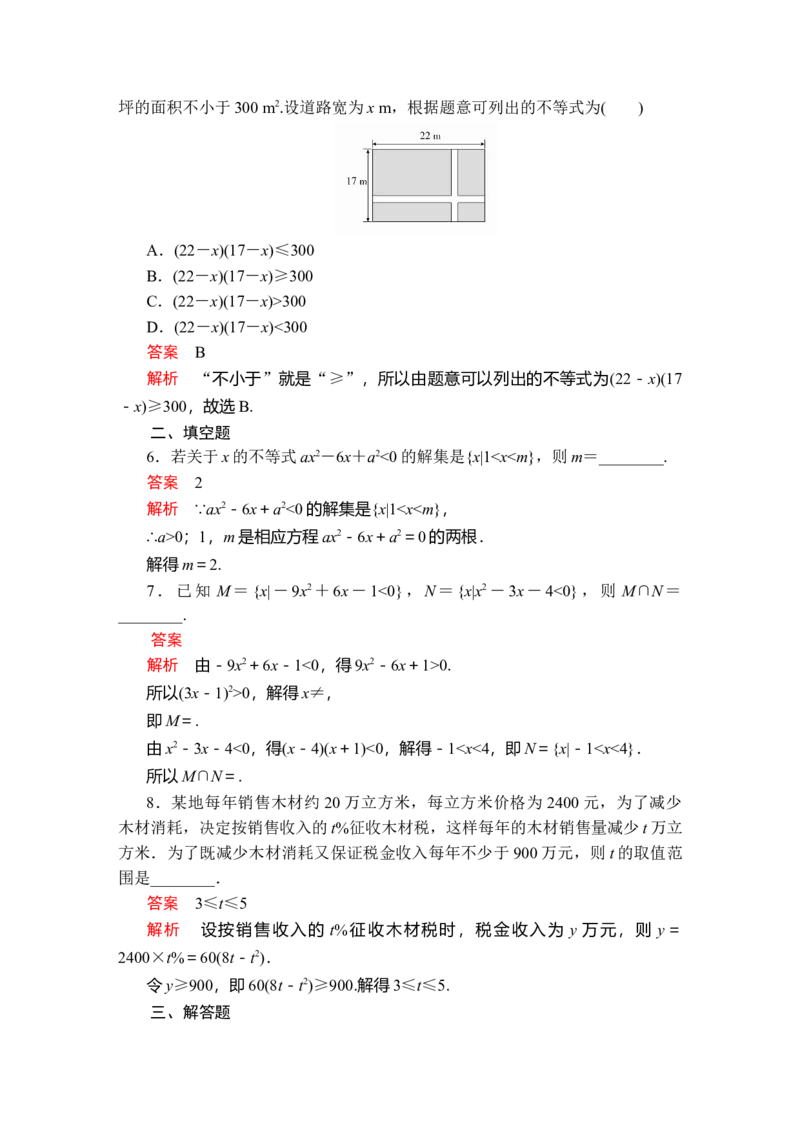
5.如图,在一块长为22 m,宽为17 m的矩形地面上,要修建同样宽的两条
互相垂直的道路(两条道路分别与矩形的一条边平行),剩余部分种上草坪,使草坪的面积不小于300 m2.设道路宽为x m,根据题意可列出的不等式为( )
A.(22-x)(17-x)≤300
B.(22-x)(17-x)≥300
C.(22-x)(17-x)>300
D.(22-x)(17-x)<300
答案 B
解析 “不小于”就是“≥”,所以由题意可以列出的不等式为(22-x)(17
-x)≥300,故选B.
二、填空题
6.若关于x的不等式ax2-6x+a2<0的解集是{x|10;1,m是相应方程ax2-6x+a2=0的两根.
解得m=2.
7.已知 M={x|-9x2+6x-1<0},N={x|x2-3x-4<0},则 M∩N=
________.
答案
解析 由-9x2+6x-1<0,得9x2-6x+1>0.
所以(3x-1)2>0,解得x≠,
即M=.
由x2-3x-4<0,得(x-4)(x+1)<0,解得-10.
(1)当m=3时,解此不等式;
(2)若对于任意的实数x,此不等式恒成立,求实数m的取值范围.
解 (1)当m=3时,不等式为x2-x-2>0.即(x-2)·(x+1)>0,解得x<-1或
x>2.
(2)设y=x2-x-m+1.∵不等式x2-x-m+1>0对于任意x都成立,∴Δ=12+
4(m-1)<0,解得m<.
故实数m的取值范围是m<.
解B级:“四能”提升训练
1.已知M是关于x的不等式2x2+(3a-7)x+3+a-2a2<0的解集,且M中
的一个元素是0,求实数a的取值范围,并用a表示出该不等式的解集.
解 原不等式可化为(2x-a-1)(x+2a-3)<0,
由x=0适合不等式得(a+1)(2a-3)>0,
所以a<-1或a>.
若a<-1,则-2a+3-=(-a+1)>5,
所以3-2a>,
此时不等式的解集是;
若a>,由-2a+3-=(-a+1)<-,
所以3-2a<,
此时不等式的解集是.2.某自来水厂的蓄水池存有400 t水,水厂每小时可向蓄水池中注水 60 t,
同时蓄水池又向居民小区不间断供水,x h内供水总量为120(0≤x≤24).
(1)从供水开始到第几个小时蓄水池中的存水量最少?最少水量是多少吨?
(2)若蓄水池中水量少于80 t时,就会出现供水紧张现象,请问:在一天的
24 h内,有几个小时出现供水紧张现象?
解 (1)设x h后蓄水池中的存水量为y t,
则y=400+60x-120(0≤x≤24),
设=u,则u2=6x(u∈[0,12]),
所以y=400+10u2-120u=10(u-6)2+40.
因为u∈[0,12],故当u=6即x=6时,y =40.
min
即从供水开始到第6 h时,蓄水池中的存水量最少,为40 t.
(2)依题意,得400+10u2-120u<80,
即u2-12u+32<0,解得4<u<8,所以16<u2<64.又u2=6x,所以16<6x
<64,所以<x<.
又-=8,所以每天约有8 h供水紧张.