文档内容
专题 5 数列中的不等式问题
新高考在试题形式、试卷结构、难度调控等方面深化改革,数列解答题的难度增加,作为压轴题出现
的概率变大,数列压轴题与不等式交汇的可能性比较大,本专题总结数列中不等式的常见类型及解法,供
大家参考.
(一)比较大小
比较 的大小,通常作差,转化为判断 与0的大小,若 ,也可以转化为判断 与1的大小.
【例1】已知数列 的前n项和 ,且满足 .
(1)求数列 的通项公式;
(2)数列 的前n项和为 ,比较 和 的大小.
【解析】(1)因为
当 时,
又因为 时, 也满足上式
所以当 时, ,
(2)由 ,得
学科网(北京)股份有限公司当 时,
当 时, , .
综上所述:当 时, ,当 时, .
(二)判断数列不等式是否成立或由数列不等式求 的范围
此类问题,一般先把所给数列不等式转化为关于n的不等式,通过解不等式或利用函数、数列性质求解.
【例2】已知数列 满足 记数列 的前 项和为 ,
(1)求证:数列 为等比数列,并求其通项 ;
(2)求 ;
(3)问是否存在正整数 ,使得 成立?说明理由.
【解析】(1) ,
即 ,
所以 ,
(2) ,所以 ,
当 为奇数时,可令 ,
则
,
学科网(北京)股份有限公司当 为偶数时,可令
则 ;
(3)假设存在正整数 ,使得 成立,
因为 , ,
所以只要
即只要满足①: ,和②: ,
对于①只要 就可以;
对于②,
当 为奇数时,满足 ,显然不成立,
当 为偶数时,满足 ,即
令 ,
因为
由于 的对称轴为 ,故 在 且 为偶数,单调递减,
当 时, ,故
即 ,且当 时, 最大,且最大值为 ,
因此, ,
所以当 为偶数时,②式成立,即当 为偶数时, 成立 .
【例3】已知数列 满足 ,且 .
学科网(北京)股份有限公司(1)设 ,证明: 是等比数列;
(2)设数列 的前n项和为 ,求使得不等式 成立的n的最小值.
【解析】(1)证明:∵ ,
, , , ,
又 , , ,
, ,
又 , , ,
,即 , ,
又 ,
, ,
∴数列 是以2为首项,2为公比的等比数列.
(2)由(1)可知数列 是以2为首项,2为公比的等比数列,
,即 ,
, ,
,又 ,
,
即 ,
学科网(北京)股份有限公司,
,
,
在 是一个增数列,
,
,
∴满足题意的n的最小值是20.
(三)根据不等式恒成立求参数范围
不等式恒成立问题,通常通过分离参数,把问题转化为 或 的形式,再利用数列单调性或函数
单调性,求 的最值,然后确定 的范围.
【例4】(2024届贵州省六盘水市高三下学期三诊)已知 为等差数列,且 , .
(1)求 的通项公式;
(2)若 恒成立,求实数λ的取值范围.
【解析】(1)设数列 的公差为d,则根据题意可得 ,
解得 ,则 .
(2)由(1)可知运用等差数列求和公式,得到 ,
又 恒成立,则 恒成立,
设 ,则 ,
当 时, ,即 ;
学科网(北京)股份有限公司当 时, ,则 ,则 ;
则 ,故 ,
故实数λ的取值范围为 .
(四)证明与通项有关的不等式
求解此类问题,一般是先确定通项,再通过放缩或数列单调性证明.
【例5】(2024届江苏省盐城市高三5月考前指导卷)在数列 的第 项与第 项之间插入 个1,称
为变换 .数列 通过变换 所得数列记为 ,数列 通过变换 所得数列记为 ,以此
类推,数列 通过变换 所得数列记为 (其中 ).
(1)已知等比数列 的首项为1,项数为 ,其前 项和为 ,若 ,求数列 的项数;
(2)若数列 的项数为3, 的项数记为 .
①当 时,试用 表示 ;
②求证: .
【解析】(1)设等比数列 的公比为 ,显然 ,
由 ,得 ,解得 .
故数列 有8项,经过1次变换后的项数为 ,
即 的项数为36.
(2)①由 的项数为 ,则当 时, ,
所以
学科网(北京)股份有限公司②因数列 是一个3项的数列,所以 ,
由 ,所以 ,
于是 ,则有
所以 ,得 ,即 ,
所以 .
, ,于是 ,
则有 ,可得 ,有 ,即 ,
所以 ,综上所述, .
(五)先求和再放缩,证明与前n项和有关的不等式
证明与前n项有关的不等式,若所给数列可以转化为等差(比)数列求和,或可以裂项求和,通常是先求和,再
放缩.
【例6】(2024届浙江省精诚联盟高三下学期适应性联考)已知等比数列 和等差数列 ,满足
, , , .
(1)求数列 , 的通项公式;
(2)记数列 的前 项和为 ,数列 的前 项和为 .证明: .
【解析】(1)等比数列 满足 , ,所以 单调递增,
设 的公比为 ,等差数列 的公差为 ,依题意可得 ,
学科网(北京)股份有限公司解得 或 (舍去),
所以 , .
(2)由(1)可得 ,
所以
所以 ,
故 ,
又 , ,
即 ,
所以
.
(六)先放缩,再求和,证明与前n项和有关的不等式
此类问题,通常是所给数列无法求和,要先把所给数列放缩成等差(比)数列或可以裂项求和、错位相减法
求和的数列,再求和,放缩时要观察待证结论,防止放缩过度或不足.
【例7】(2024届广西柳州高级中学高三下学期3月热身考) 表示正整数a,b的最大公约数.若
学科网(北京)股份有限公司,且 ,则将k的最大值记为 ,例如:
(1)求 ;
(2)设 ,数列 的前n项和为 证明:
【解析】(1)依题可得 表示所有不超过正整数m,且与m互质的正整数个数.
因为与2互质的数为1,所以 ,
因为与3互质的数为1,2,所以 ,
因为在 中与 互质的正整数只有 ,
所以在 中与 互质的正整数的个数为 ,因此 ;
(2) ,则 ,
因为 ,
所以 ,因此有 ,
所以 ,
因为 ,所以 .
【例8】(2024届云南省大理新世纪中学高三数学模拟)自然常数,符号 ,为数学中的一个常数,是一个无限
不循环小数,且为超越数,其值约为2.71828.它是自然对数的底数.有时称它为欧拉数(Euler number),以瑞士
数学家欧拉命名;也有个较为少见的名字“纳皮尔常数”,以纪念苏格兰数学家约翰・纳皮尔(John
Napier)引进对数.它就像圆周率 和虚数单位 ,是数学中最重要的常数之一,它的其中一个定义是
学科网(北京)股份有限公司.设数列 的通项公式为 , ,
(1)写出数列 的前三项 , , .
(2)证明: .
【解析】(1)由通项公式得,
; ; .
(2)由二项式定理得
,
所以 是 上的单调递增数列,
因为 ,则 ;
又
,
学科网(北京)股份有限公司综上可知, .
(七)借助导数证明与前n项和有关的不等式.
求解此类问题,通常先利用导数证明一个不等式,再把不等式中的自变量用 代换,通过累加或累乘法
证明所给不等式.
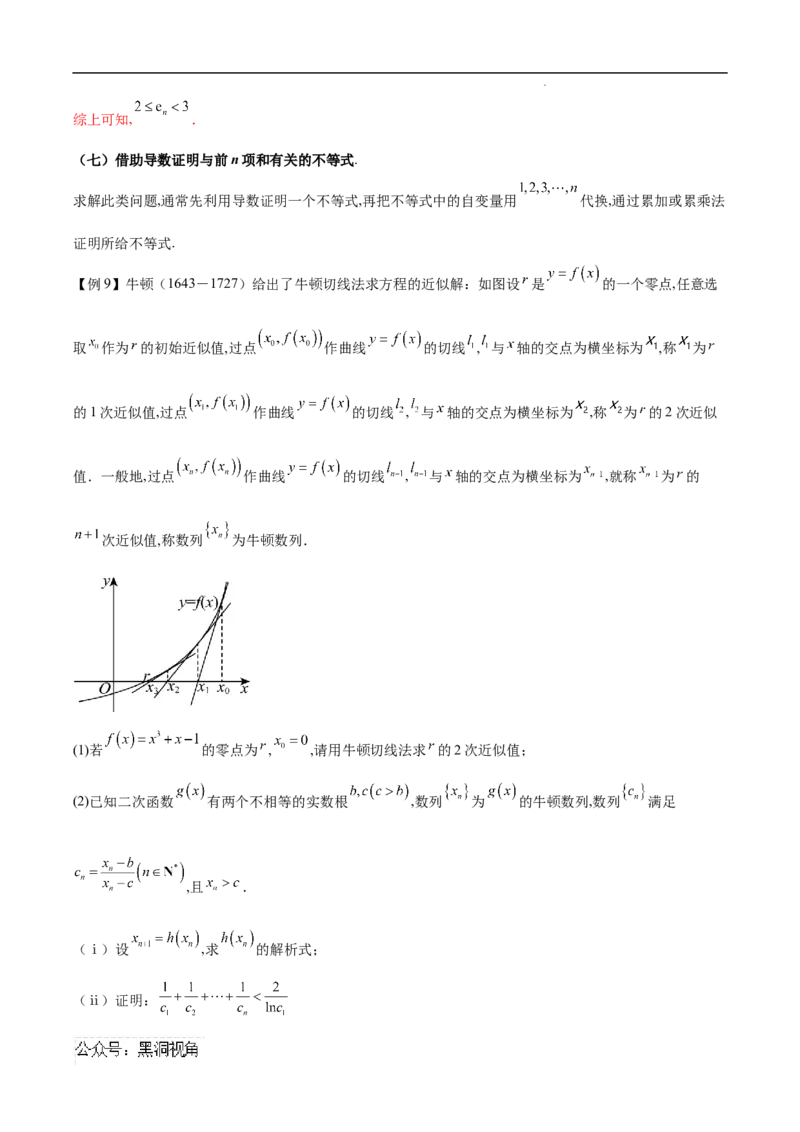
【例9】牛顿(1643-1727)给出了牛顿切线法求方程的近似解:如图设 是 的一个零点,任意选
取 作为 的初始近似值,过点 作曲线 的切线 , 与 轴的交点为横坐标为 ,称 为
的1次近似值,过点 作曲线 的切线 , 与 轴的交点为横坐标为 ,称 为 的2次近似
值.一般地,过点 作曲线 的切线 , 与 轴的交点为横坐标为 ,就称 为 的
次近似值,称数列 为牛顿数列.
(1)若 的零点为 , ,请用牛顿切线法求 的2次近似值;
(2)已知二次函数 有两个不相等的实数根 ,数列 为 的牛顿数列,数列 满足
,且 .
(ⅰ)设 ,求 的解析式;
(ⅱ)证明:
学科网(北京)股份有限公司【解析】(1)
,所以
当 ,所以
当 ,
所以 的2次近似值为 .
(2)(ⅰ)因为二次函数 有两个不等实根 ,
所以不妨设 ,
则 ,
因为 所以
所以在横坐标为 的点处的切线方程为
令 则
即 ,
所以 .
(ⅰⅰ)由(ⅰ)知,
所以 .
因为 所以 所以 .
学科网(北京)股份有限公司令 则 ,又
所以 ,数列 是公比为2的等比数列.
.
令 ,则
当 时, ,所以 在 单调递减,
所以 ,即
因为 所以 即 .
.
【例1】(2024届山东省泰安肥城市高考仿真模拟)在足球比赛中,有时需通过点球决定胜负.
(1)扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将
(也称为守门员)也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也
有 的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数 的分布列
和期望;
(2)好成绩的取得离不开平时的努力训练,甲、乙、丙三名前锋队员在某次传接球的训练中,球从甲脚下开始,等
可能地随机传向另外 人中的 人,接球者接到球后再等可能地随机传向另外 人中的 人,如此不停地传下
学科网(北京)股份有限公司去,假设传出的球都能接住.记第 次传球之前球在甲脚下的概率为 ,易知 .
① 试证明: 为等比数列;
② 设第 次传球之前球在乙脚下的概率为 ,比较 与 的大小.
【解析】(1)解法一:依题意可得,门将每次可以扑到点球的概率为 ,
门将在前三次扑到点球的个数 可能的取值为
易知 ,所以
故 的分布列为:
0 1 2 3
所以 的数学期望 .
解法二: 的所有可能取值为
在一次扑球中,扑到点球的概率 ,
所以
所以 的分布列如下:
0 1 2 3
学科网(北京)股份有限公司所以的 数学期望:
(2)①第 次传球之前球在甲脚下的概率为 ,
则当 时,第 次传球之前球在甲脚下的概率为 ,
第 次传球之前球不在甲脚下的概率为 ,
则
即 ,又 ,
所以 是以 为首项,公比为 的等比数列.
②由①可知 ,所以 ,
所以 ,故 .
【例2】(2024届陕西省西北工业大学附中高三适应性训练)已知函数
(1)若函数在 内点 处的切线斜率为 ,求点 的坐标;
(2)①当 时,求 在 上的最小值;
②证明: .
【解析】(1)设点 .
由于 ,则 ,得 ,
学科网(北京)股份有限公司则 ,且 ,所以点 的坐标为 .
(2)① ,
则 ,记 ,
则
易知 在 上单调递减,且 ,
,即 ,
所以,当 时, , 在 上单调递增;
当 时, , 在 上单调递减.
因为 ,
所以 时, , 在 单调递增,
所以,当 时, 取得最小值 .
②由①可知 ,时 恒成立,即 恒成立.
设 ,则 ,
当 时, , 在 上单调递增,
所以 ,所以 ,
学科网(北京)股份有限公司又 ,所以 ,
取 ,则 ,
,得证.
【例3】(2024届重庆市开州中学高三下学期模拟)设有穷数列 的项数为 ,若正整数
满足: ,则称 为数列 的“ 点”.
(1)若 ,求数列 的“ 点”;
(2)已知有穷等比数列 的公比为 ,前 项和为 .若数列 存在“ 点”,求正数 的取值范
围;
(3)若 ,数列 的“ 点”的个数为 ,证明: .
【解析】(1)因为
所以 ,
所以数列 的 “ 点” 为 3,5 ,
(2)依题意, ,因为数列 存在 “ 点”,
所以存在 ,使得 ,
所以 ,即 .
学科网(北京)股份有限公司因为 ,所以 ,所以 ,
又 随 的增大而增大,
所以当 时, 取最大值 ,
所以 ,又 ,所以 .
当 时,有 ,
所以数列 存在 “ 点”,所以 的取值范围为 ,
(3)①若 ,则数列 不存在 “ 点”,即 .
由 得, ,所以 ,
②若存在 ,使得 . 下证数列 有 “ 点”.
证明: 若 ,则2是数列 的 “ 点”;
若 ,因为存在 ,使得 ,
所以设数列 中第1个小于 的项为 ,
则 ,所以 是数列 的第1个 “ 点”.
综上,数列 存在 “ 点”.
不妨设数列 的 “ 点” 由小到大依次为 ,
则 是 中第1个小于 的项,
故 ,因为 ,
学科网(北京)股份有限公司所以 ,所以 ,所以
所以
所以 .综上, ,得证.
【例4】(2024届天津市河北区高三质量检测二)已知 是等差数列,其前 项和为 是等比数列,已
知 , 是 和 的等比中项.
(1)求 和 的通项公式;
(2)求数列 的前 项和 ;
(3)记 ,求证: .
【解析】(1)由题意 ,
,
又 是 和 的等比中项,得 ,
又 ,解得 ,
;
(2) ,设 ,
学科网(北京)股份有限公司则 ,
将以上两式相减得
,
;
(3)
,
,
.
结论得证.
【例5】如图,已知点列 在曲线 上,点列 在x轴上, , , 为等腰
直角三角形.
学科网(北京)股份有限公司(1)求 , , ;(直接写出结果)
(2)求数列 的通项公式;
(3)设 ,证明: .
【解析】(1)由 为等腰直角三角形,所以直线 的直线斜率为1,
故直线 的方程为 ,与抛物线方程联立可得 ,可解得 或 ,
从而可得 ,可得 的横坐标为1,因为 ,解得 ,
由 ,所以 ,可得 ,
可得 ,解得 ;
(2)由题意可得 ,所以 ,
所以 ,所以 ,
所以 ,
学科网(北京)股份有限公司所以 是以 为首项, 为公差的等差数列,
所以 ,所以 ,
(3)由(1)可得 ,
所以 ,
所以 ,
,
所以 .
1.(2024届新疆喀什地区高三5月适应性检测)已知数列 的首项 ,且满足 (
).
(1)求证:数列 为等比数列;
(2)记 ,求数列 的前 项和 ,并证明 .
2.(2024届山东省济钢高级中学高三5月适应性考试)已知复数数列 的通项公式为 ( 是虚
数单位), 为 的前 项和.
(1)求 的值;
学科网(北京)股份有限公司(2)求证: ;
(3)求 的通项公式.
3.已知数列 满足 .
(1)证明 是等比数列,并求 的通项公式;
(2)证明:
4.已知函数 ,数列 满足 正整数
(1)求 的最大值;
(2)求证: ;
(3)求证: .
5.(2024届天津市南开区高三下学期质量监测二)已知函数 , .
(1)求曲线 在 处的切线方程;
(2)证明:对 , 恒成立( 为 的导数);
(3)设 ,证明: ( ).
6.(2025届江西省多所学校高三第一次大联考)定义:若对于任意 ,数列 满足:① ;
② ,其中 的定义域为 ,则称 关于 满足性质 .
(1)请写出一个定义域为 的函数 ,使得 关于 满足性质 ;
学科网(北京)股份有限公司(2)设 ,若 关于 满足性质 ,证明: ;
(3)设 ,若 关于 满足性质 ,求数列 的前 项和.
7.(2024届湖南省岳阳市湘阴县第一中学高三下学期期中)设数列 的前 项和为 ,且 .
(1)求数列 的通项公式 .
(2)设数列 满足 ,且数列 的前 项和为 ,求证: .
8.(2024届陕西省铜川市王益中学高三下学期模拟)不透明的袋子中装有大小相同的白球和彩球各1个,
将“连续两次从袋子中有放回地摸出1个小球”记为一次试验,若两次均摸到彩球,则试验成功并终止试验,
否则在袋子中添加一个相同的白球,然后进行下一次试验.
(1)若最多只能进行3次试验,设试验终止时进行的次数为随机变量 ,求 的分布列与数学期望;
(2)若试验可以一直进行下去,第 次试验成功的概率记为 ,求证: .
9.(2024届湖南省娄底市高三下学期高考考前仿真联考)已知等比数列 的各项都为正实数,
.
(1)求数列 的通项公式;
(2)设 ,数列 的前 项和为 ,证明: .
10.(2024届广西贵港市高考模拟预测)某射击运动员进行射击训练,已知其每次命中目标的概率均为 .
(1)若该运动员共射击6次,求其在恰好命中3次的条件下,第3次没有命中的概率;
(2)该运动员射击训练不超过n( )次,当他命中两次时停止射击(射击n次后,若命中的次数不足两
次也不再继续),设随机变量X为该运动员的射击次数,试写出随机变量X的分布列,并证明 .
11.(2024届福建省泉州第一中学高三下学期适应性测试)已知有穷正项数列 ,若将每个项依
次围成一圈,满足每一项的平方等于相邻两项平方的乘积,则称该数列可围成一个“HL-Circle”.例如:数列
学科网(北京)股份有限公司都可围成“HL-Circle”.
(1)设 ,当 时,是否存在 使该数列可围成“HL-Circle”,并说明理由:
(2)若 的各项不全相等,且可围成“HL-Circle”.
(i)求 的取值集合;
(ii)求证: .
12.已知数列 中, ,设 为 前 项和, ,已知数列 ,设 的前 项和 .
(1)求 ;
(2)若 对任意 恒成立,求实数 的取值范围.
13.(2024届河北省邢台市部分高中二模)已知数列 的前 项和为 ,且 .
(1)求数列 的通项公式;
(2)求证: .
14.(2024届江西省宜丰中学高三下学期模拟)设 , .
(1)当 时,证明: ;
(2)证明: .
15.(2024届江苏省扬州中学高三下学期全真模拟)帕德近似是法国数学家帕德发明的用多项式近似特定
函数的方法.给定两个正整数m,n,函数 在 处的 阶帕德近似定义为:
,且满足: , , ,…, .注:
学科网(北京)股份有限公司, , , ,…已知 在 处的
阶帕德近似为 .
(1)求实数a,b的值;
(2)当 时,试比较 与 的大小,并证明;
(3)已知正项数列 满足: , ,求证: .
学科网(北京)股份有限公司