文档内容
更多全科试卷,请关注公众号:高中试卷君
2024 届高三二轮复习“8+3+3”小题强化训练(16)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.已知集合 ,则 ( )
A. B.
C. D.
【答案】C
【解析】 ,
,
则 .
故选:C.
2.某班的全体学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为 ,
, , .若低于60分的人数是15,则该班的学生人数是( )
A. 40 B. 45 C. 50 D. 60
【答案】C
【解析】由频率分布直方图可得低于60分的人的频率为 ,
由于低于60分的人数是15,则该班的学生人数是 ,
故选:C
3.已知直线 与曲线 在点 处的切线垂直,则直线 的斜率为( )
A. -1 B. 1 C. D. 2
【答案】C
【解析】由函数 ,可得 ,
则 ,所以直线 的斜率为 .
故选:C.
4.若数列 的前 项和 ,则数列 的前 项和 ( )
A. B. C. D.
【答案】C
【解析】因为数列 的前 项和 ,更多全科试卷,请关注公众号:高中试卷君
所以当 时, ,两式相减,得
,
当 时, 也符合该式,所以 ,
,
所以数列 是首项为12,公差为12的等差数列,
所以 .
故选:C.
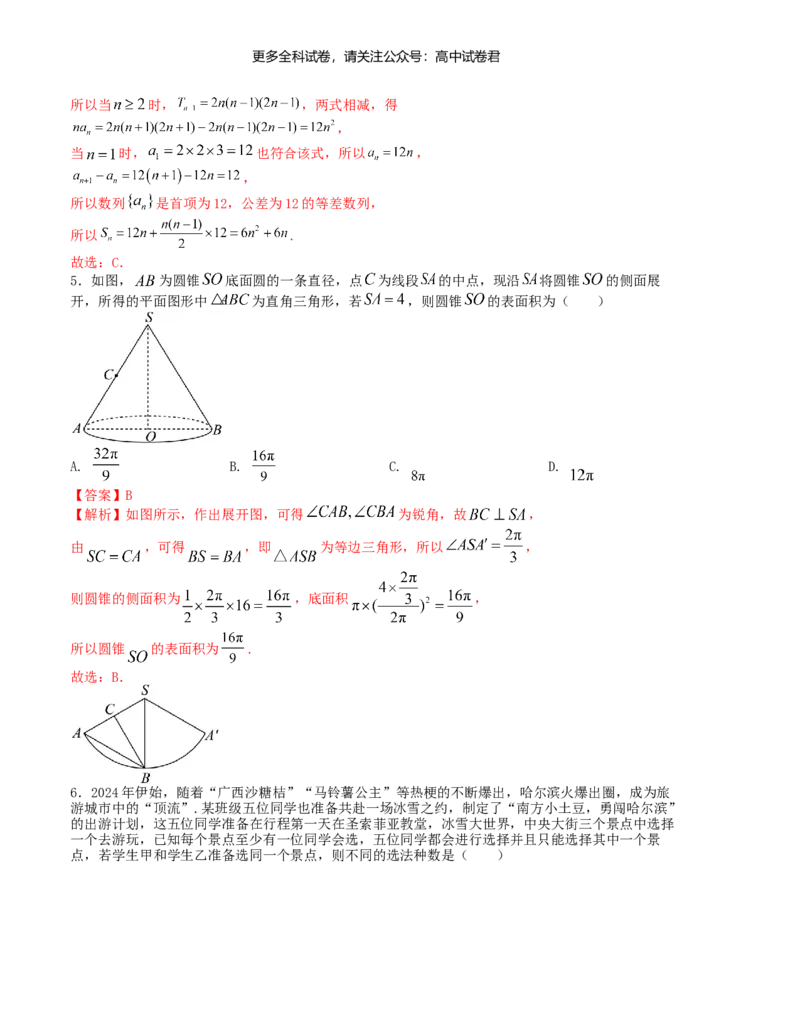
5.如图, 为圆锥 底面圆的一条直径,点 为线段 的中点,现沿 将圆锥 的侧面展
开,所得的平面图形中 为直角三角形,若 ,则圆锥 的表面积为( )
A. B. C. D.
【答案】B
【解析】如图所示,作出展开图,可得 为锐角,故 ,
由 ,可得 ,即 为等边三角形,所以 ,
则圆锥的侧面积为 ,底面积 ,
所以圆锥 的表面积为 .
故选:B.
6.2024年伊始,随着“广西沙糖桔”“马铃薯公主”等热梗的不断爆出,哈尔滨火爆出圈,成为旅
游城市中的“顶流”.某班级五位同学也准备共赴一场冰雪之约,制定了“南方小土豆,勇闯哈尔滨”
的出游计划,这五位同学准备在行程第一天在圣索菲亚教堂,冰雪大世界,中央大街三个景点中选择
一个去游玩,已知每个景点至少有一位同学会选,五位同学都会进行选择并且只能选择其中一个景
点,若学生甲和学生乙准备选同一个景点,则不同的选法种数是( )更多全科试卷,请关注公众号:高中试卷君
A. 54 B. 21 C. 18 D. 36
【答案】D
【解析】若甲乙选的景点没有其他人选,则分组方式为: 的选法总数为: ,
若甲乙选的景点还有其他人选择,则分组方式为: 的选法总数为: ,
所以不同的选法总数为: .
故选:D.
7.已知 ,则 的值为( )
A. B. C. D.
【答案】A
【解析】由 ,得 ,
所以 ,
,
所以
,
故选:A
8.若 , , ,则( )
A. B. C. D.
【答案】D
【解析】令 , , ,
, ,
则 ,
令 , ,当 时, ,所以 在 时单调递
增,更多全科试卷,请关注公众号:高中试卷君
所以当 时, ,
所以 在 时单调递减,所以 ,所以 ;
当 时, ,令 ,则 ,
所以 在 上单调递增,所以 ,
所以 在 上单调递增,
所以 ,所以 ,
综上, .
故选:D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.用“五点法”作函数 ( , , )在一个周期内的图象
时,列表计算了部分数据,下列有关函数 描述正确的是( )
0
x a b c
1 3 1 d 1
A. 函数 的最小正周期是
B. 函数 的图象关于点 对称
C. 函数 的图象关于直线 对称
D. 函数 与 表示同一函数
【答案】ACD
【解析】根据表格可知 ,且 ,则 ,
由正弦函数的周期性可知 的最小正周期为 ,故A正确;更多全科试卷,请关注公众号:高中试卷君
由已知结合正弦函数的对称性可知:
,
显然 此时取得最小值,所以 的图象不关于点 对称,故B错误;
由已知结合正弦函数的对称性可知:
,此时 取得最大值,
所以 的图象关于直线 对称,故C正确;
由诱导公式可知 ,故D正确.
故选:ACD
10.已知 为复数,设 , , 在复平面上对应的点分别为A,B,C,其中O为坐标原点,则
( )
A. B.
C. D.
【答案】AB
【解析】设 , ,
, ,
, ,
对于A, ,故选项A正确;
对于B, , ,故选项B正确;
对于C, ,
当 时, ,故选项C错误;
对于D, ,
可以为零,也可以不为零,所以 不一定平行于 ,故选项D错误.
故选:AB.
11.定义在 上的函数 同时满足① ;②当 时,
,则( )
A.
B. 为偶函数
C. 存在 ,使得更多全科试卷,请关注公众号:高中试卷君
D. 对任意
【答案】ACD
【解析】对于A, ,令 ,则 ,即
,又 , ,即 ,
可知 ,即 ,得 即 ,故A正确;
对于B,由选项A可得 ,又令 得 ,解得 ,
,
所以函数 不是偶函数,故B错误;
对于C,因为 ,当 时,
,又 满足上式,
, ,令 ,则 ,
所以存在 ,使得 ,故C正确;
对于D,令 ,
则
,即 ,即 是以1为周期的周期函数,因为当
, ,
则 ,
当且仅当 且 与 异号时等号成立,但 ,故 与2同号,
故等号不成立,故
结合周期性可知对任意 ,均有 ,
所以 ,故D正确.
故选:ACD.
三、填空题:本题共3小题,每小题5分,共15分.
12.已知向量 , 为单位向量,且满足 ,则向量 在向量 方向的投影向
量为________
【答案】更多全科试卷,请关注公众号:高中试卷君
【解析】因为 ,所以 ,即 ,
又 , 为单位向量,则 , ,
所以向量 在向量 方向的投影向量为 .
故答案为:
13.若正四面体 的顶点都在一个表面积为 的球面上,过点 且与 平行的平面 分别与
棱 交于点 ,则空间四边形 的四条边长之和的最小值为__________.
【答案】 ##
【解析】如图,将正四面体放置到正方体中,易知正四面体外接球即正方体的外接球,
设正四面体 的棱长为 ,所以正方体的边长为 ,
易知正方体的外接球直径为体对角线 的长,又 ,所以正四面体的半径
,
依题有 ,得到 ,即正四面体 的棱长为 ,
因为 面 ,面 面 , 面 ,所以 ,
设
因为 ,则 , ,
在 中,因为 ,所以 ,
在 中, , ,则
,
所以空间四边形 的四条边长之和
,
又 ,当 时, ,更多全科试卷,请关注公众号:高中试卷君
故答案为: .
14.已知 是双曲线 上任意一点,若 到 的两条渐近线的距离之积为 ,则
上的点到焦点距离的最小值为__________.
【答案】
【解析】所求的双曲线方程为 ,则渐近线方程为 ,
设点 ,则 ,
点 到 的两条浙近线的距离之积为 ,
解得: ,故双曲线 方程为: ,
故 ,故双曲线 上的点到焦点距离的最小值为 .
故答案为: .