文档内容
专练 05(填空题-提升)
1.(2019·江苏省海头高级中学高一期中)定义域 为的函数 满足 且
,则 _______.
【答案】1
【分析】
根据题意可得 ,从而求得 的值.
【详解】
解: 函数 满足 , 且 ,
,
故答案为: .
【点睛】
本题考查根据函数的性质求函数的值,属于基础题.
2.若函数 的定义域为 ,则函数 的定义域为______.
【答案】 .
【分析】
由f(2x+1)的定义域得x的取值范围,求出2x+1的取值范围,即函数 中 的范围,从而解出x即为函数 的定义域.
【详解】
由 的定义域为 ,得 的定义域为 ,即 ,
由 得 , 的定义域为 .
故答案为: .
【点睛】
本题考查复合函数的定义域求法,根据函数定义域之间的关系求解即可,注意函数的定义域始终为自变量
x的范围这一概念,属于基础题.
3.有下列几个命题:
①函数 在 上是增函数;
②函数 在 上是减函数;
③函数 的单调区间是 ;
④已知 在 上是增函数,若 ,则有 .
其中正确命题的序号是__________.
【答案】①④
【分析】
对于①,直接由二次函数的单调性加以判断;
对于②,错误在于两个减区间取了并集;对于③,先求出函数的定义域,再结合二次函数的单调性求单调区间;
对于④,直接利用增函数的定义判断.
【详解】
对于①,函数y=2x2+x+1对应的图象是开口向上的抛物线,且对称轴方程为x ,
∴函数y=2x2+x+1在(0,+∞)上是增函数.命题①正确;
对于②,函数y 的图象是把 的图象向左平移1个单位得到的,
而 的减区间是(﹣∞,0),(0,+∞),
∴函数y 在(﹣∞,﹣1),(﹣1,+∞)上是减函数.命题②错误;
对于③,由5+4x﹣x2≥0,得:﹣1≤x≤5.
函数g(x)=﹣x2+4x+5对应的图象开口向下,且对称轴方程为x=2.
∴函数y 的单调增区间是[﹣1,2],减区间是(2,5].命题③错误;
对于④,∵a+b>0,
∴a>﹣b,b>﹣a.
又f(x)在R上是增函数,
∴f(a)>f(﹣b),f(b)>f(﹣a).
则f(a)+f(b)>f(﹣a)+f(﹣b).命题④正确.
故答案为①④
【点睛】本题考查命题的真假判断与应用,考查了二次函数的单调性,是中档题.
4.(2019·广东石门中学高一月考) ___________.
【答案】
【分析】
直接利用指数幂的运算法则求解即可,求解过程注意避免计算错误.
【详解】
.
故答案为:
【点睛】
化简原则:①化根式为分数指数幂;②化负指数幂为正指数幂;③化小数为分数;④注意运算的先后顺
序,属于较易题目.
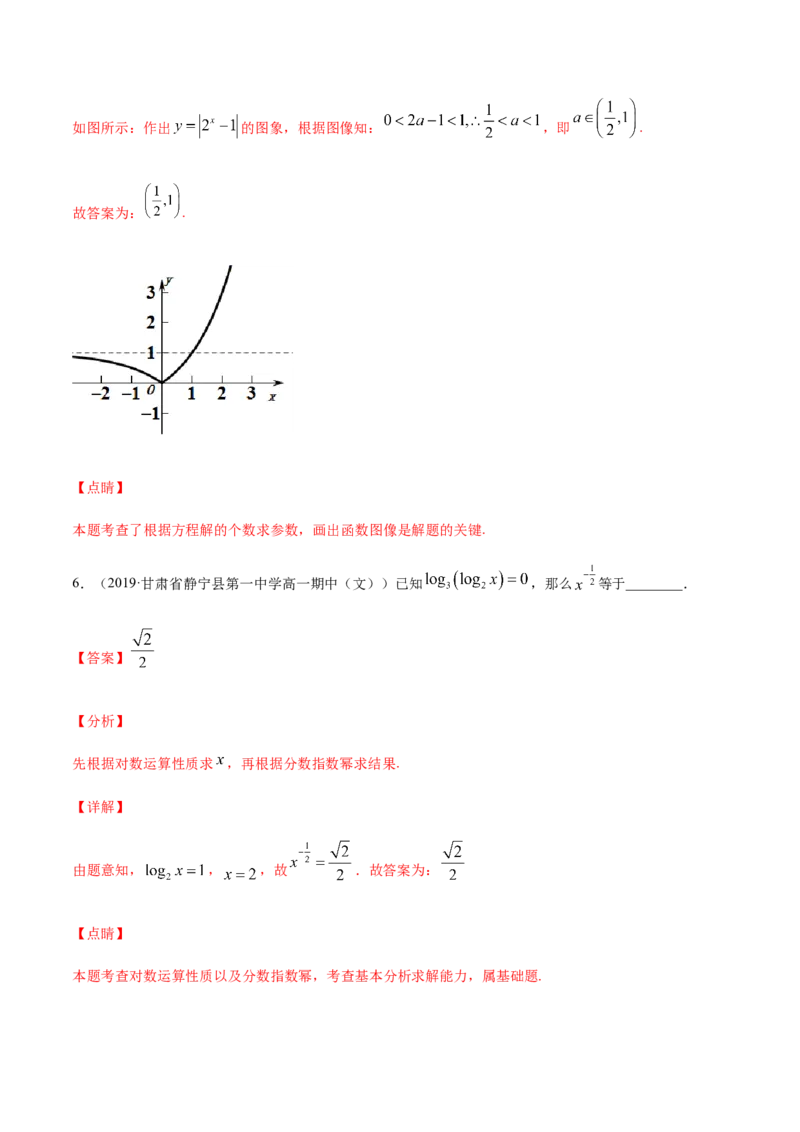
5.已知方程 有两个不等实根,则实数 的取值范围为____________.
【答案】
【分析】
画出函数 的图像,根据图像得到答案.
【详解】如图所示:作出 的图象,根据图像知: ,即 .
故答案为: .
【点睛】
本题考查了根据方程解的个数求参数,画出函数图像是解题的关键.
6.(2019·甘肃省静宁县第一中学高一期中(文))已知 ,那么 等于________.
【答案】
【分析】
先根据对数运算性质求 ,再根据分数指数幂求结果.
【详解】
由题意知, , ,故 .故答案为:
【点睛】
本题考查对数运算性质以及分数指数幂,考查基本分析求解能力,属基础题.7.已知 ,则 _________.
【答案】
【分析】
利用同角的三角函数的基本关系式可把 化为 ,从而可
求前者的值.
【详解】
因为 ,故 ,
故答案为: .
【点睛】
本题考查同角的三角函数的基本关系式,一般地,对于给值求值的问题,需结合给定的代数式的特征进行
合理变形,如二次式可以利用平方关系转化为齐次式,再利用商数关系转化为关于 的代数式.
8.(2020·安徽六安一中高一月考)函数 的最大值为________.
【答案】
【分析】将解析式化为 ,再利用基本不等式,即可得答案;
【详解】
,等号成立当且仅当 ,
故答案为: .
9.(2020·浙江诸暨中学高一月考)已知函数 为奇函数, 为偶函数,且 ,
则 _____________.
【答案】
【分析】
利用函数的奇偶性求出 和 的解析式,即可求 .
【详解】
因为函数 为奇函数, 为偶函数, ①,
所以 ,即 ②,
①+②得: ,所以 ,所以 ,
故答案为:
【点睛】
本题主要考查了利用函数的奇偶性求函数的解析式和函数值,属于基础题.
10.若函数 是定义在 上的奇函数, ,当 时, ,则实数
_______.
【答案】1
【分析】
由函数是奇函数,求得 ,代入 的解析式,即求得 .
【详解】
是定义在 上的奇函数, ,
又 时, , , .
故答案为:1.
【点睛】
本题注意考查函数的奇偶性,利用点对称求得 的值.
11.(2016·上海格致中学高一期中)已知集合 满足,集合 ,,则 ________.
【答案】
【分析】
化简集合 ,求出两集合的交集即可.
【详解】
由集合A中的函数 ,得到集合
由集合B中的函数 ,集合 ,
则
故答案为: .
【点睛】
本题主要考查了交集及其运算,属于基础题.
12.已知关于 的不等式 的解集是 ,则 _____.
【答案】
【分析】
先由题意得到不等式 等价于 ,不等式的解集得到 和 是关于 的方程
的两个根,进而可求出结果.【详解】
因为不等式 等价于 ,又其解集是 ,
所以 和 是关于 的方程 的两个根,因此 ,解得 ,
故答案为
【点睛】
本题主要考查由不等式的解集求参数的问题,熟记三个二次之间关系即可,属于常考题型.
13. 为第四象限角,化简: ________.
【答案】
【分析】
由 为第四象限角,得出 , ,再利用同角三角函数的基本关系式化简,进而得解.
【详解】
为第四象限角, , ,
故答案为: .
【点睛】
本题主要考查的是同角三角函数的基本关系式,其中涉及到由角的范围确定三角函数值的符号,属于基础
题.14.已知 ,则 的最小值为______.
【答案】 .
【分析】
用“1”的代换法配凑出定值,然后用基本不等式得最小值.
【详解】
,当且仅当 ,解得
,又因为 ,所以 时等号成立.
故答案为: .
【点睛】
本题考查用基本不等式求最值,解题关键是要配凑出定值,“1”的代换是常用方法.用基本不等式求最值
时一定要注意等号成立的条件是否能满足.
15.(2020·安徽省临泉第二中学高三月考(理))设函数 ,则 ______.
【答案】1
【分析】
根据题中分段函数的对应关系,先计算 ,再计算 即得解.
【详解】由题意,
故答案为:1
【点睛】
本题考查了求分段函数的函数值,考查了学生概念理解,数学运算的能力属于基础题.
16.已知函数 ,若 ,则实数 的取值范围是__________.
【答案】{ 且 }
【分析】
利用指数函数与对数函数的单调性判断 在定义域内为增函数,利用函数的单调性可得 ,
解不等式组即可.
【详解】
因为 在定义域 内单调递增,
所以 即{ 且 }
故答案为:{ 且 }
【点睛】
本题考查了指数函数、对数函数的单调性、利用函数的单调性解不等式,属于基础题.
17.(2019·安徽芜湖一中高一期中)已知集合 , , ,则_______.
【答案】
【分析】
因为集合 , ,根据 ,可得 和 ,此时集合 ,集合
,此时必有 ,解得 或 ,结合已知,即可求得答案.
【详解】
,可得 ,即
此时集合 ,集合 , 此时必有 ,解得 或
当 时,集合 不成立,舍去;
当 时,集合 成立. ,
故答案为: .
【点睛】
本题考查了根据集合相等求参数,解题关键是掌握集合相等的定义,考查了分析能力和计算能力,属于基础题.
18.(2020·沭阳县修远中学高一月考)已知 是 上的增函数,则实数 的取值
范围是__________.【答案】
【分析】
由 解得结果即可得解.
【详解】
因为 是 上的增函数,所以 ,解得 .
故答案为: .
【点睛】
本题考查了根据分段函数的单调性求参数的取值范围,属于基础题.
19.(2020·江西高一期中)若 ,则 __________.
【答案】
【分析】
利用换元法运算即可得解.
【详解】
由题意, ,设 ,则 ,所以 .故答案为: .
20.已知函数 , ,若 ,则 的
值域是______.
【答案】 .
【分析】
由题意求出 ,注意 的范围,问题得以解决.
【详解】
解: 函数 ,
, ,
在 上单调递增,
的值域是 .
故答案为:
【点睛】
本题主要考查了函数的值域,幂函数的性质,关键是注意自变量的取值范围,属于基础题.