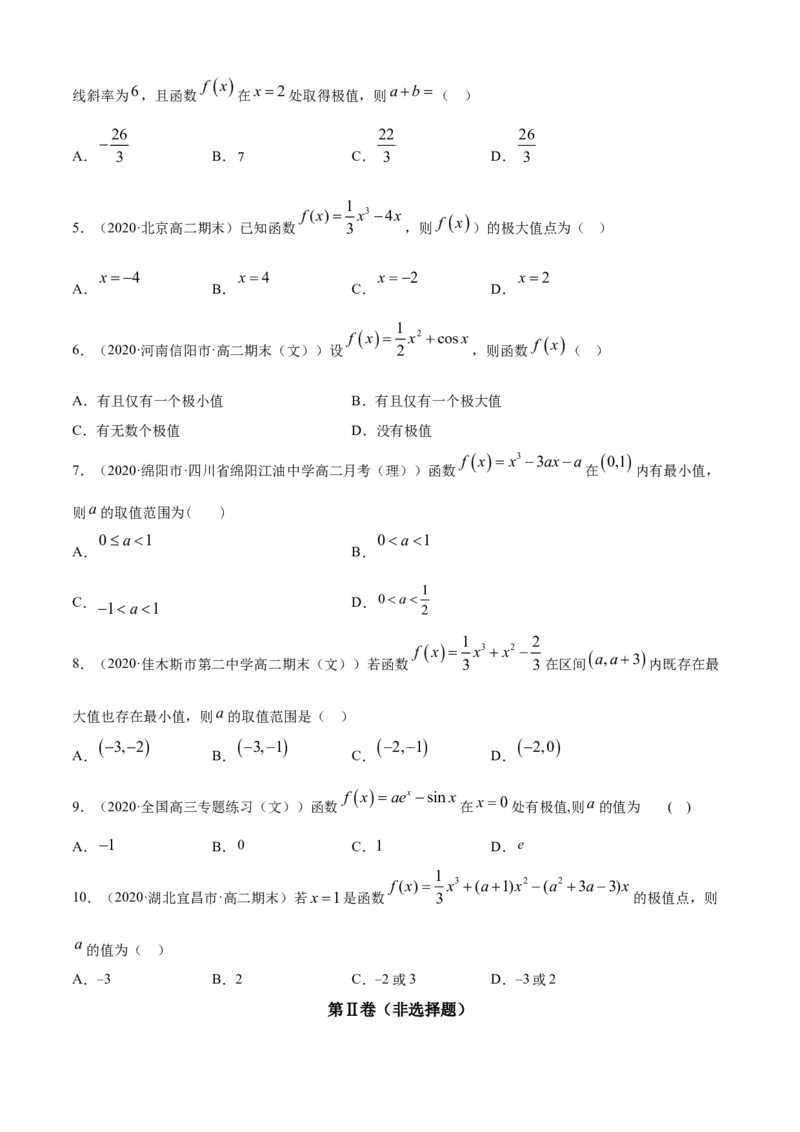专题5.3导数在研究函数中的应用（2）（A卷基础篇）原卷版_E015高中全科试卷_数学试题_选修2_01.同步练习_同步练习（第四套）_专题5.3导数在研究函数中的应用（2）（A卷基础篇）

专题5. 3导数在研究函数中的应用（2）（A卷基础篇） （新教材人教A版,浙江专用） 参考答案与试题解析 第Ⅰ卷（选择题） 一．选择题（共10小题，满分50分，每小题5分） f(x) [a,b] (a,b) 1．（2020·全国高二课时练习）设 是区间 上的连续函数，且在 内可导，则下列结论中正 确的是（ ） f(x) A． 的极值点一定是最值点 f(x) B． 的最值点一定是极值点 f(x) [a,b] C． 在区间 上可能没有极值点 f(x) [a,b] D． 在区间 上可能没有最值点 2．（2020·全国高二单元测试）如图是函数y＝f（x）的导数y＝f'（x）的图象，则下面判断正确的是（ ） A．在（﹣3，1）内f（x）是增函数 B．在x＝1时，f（x）取得极大值 C．在（4，5）内f（x）是增函数 D．在x＝2时，f（x）取得极小值 f(x)lnxax x2 a 3．（2020·横峰中学高三月考（文））已知函数 在 处取得极值，则 （ ） 1 A．1 B．2 C． D．-2 2 f xax3bx1 1,ab1 4．（2020·霍邱县第二中学高二月考（文））已知函数 的图象在点 处的切f x 6 x2 ab 线斜率为 ，且函数 在 处取得极值，则 （ ） 26 22 26  A． 3 B．7 C． 3 D． 3 1 f(x) x34x f x 5．（2020·北京高二期末）已知函数 3 ，则 ）的极大值点为（ ） x4 x4 x2 x2 A． B． C． D． 1 f x x2 cosx f x 6．（2020·河南信阳市·高二期末（文））设 2 ，则函数 （ ） A．有且仅有一个极小值 B．有且仅有一个极大值 C．有无数个极值 D．没有极值 f x x3 3axa 0,1 7．（2020·绵阳市·四川省绵阳江油中学高二月考（理））函数 在 内有最小值， 则a的取值范围为( ) 0a1 0a1 A． B． 1 C． D．0a 1a1 2 1 2 f x x3 x2  a,a3 8．（2020·佳木斯市第二中学高二期末（文））若函数 3 3 在区间 内既存在最 大值也存在最小值，则a的取值范围是（ ） 3,2 3,1 2,1 2,0 A． B． C． D． f xaex sinx x0 a 9．（2020·全国高三专题练习（文））函数 在 处有极值,则 的值为 ( ) A．1 B．0 C．1 D．e 1 f(x) x3(a1)x2 (a2 3a3)x 10．（2020·湖北宜昌市·高二期末）若x1是函数 3 的极值点，则 a 的值为（ ） A．-3 B．2 C．-2或3 D．–3或2 第Ⅱ卷（非选择题）二．填空题（共7小题，单空每小题4分，两空每小题6分，共36分） 11．（2020·四川成都市·高三开学考试（文））已知函数 ，则 在 上的最小 值是_______________. 12．（2020·昆明呈贡新区中学（云南大学附属中学呈贡校区）高三月考（理））若x＝2是f(x)＝ax3-3x的 一个极值点，则a＝________. 13．（2019·浙江高三专题练习）若函数 在 ，则函数的最小值是 _______ ；最大值 是_________. 14．（2020·东台创新高级中学高二月考）已知函数 ，则 的极小值为______． 15．（2019·西藏拉萨市·拉萨那曲第二高级中学高二月考（文））函数 的极值是： ________和________. 16．（2019·浙江绍兴市·高二期末）函数 （其中 …是自然对数的底数）的 极值点是________；极大值 ________. 17．（2020·全国高三专题练习）设 是奇函数 的导函数， ，且对任意 都有 ，则 _________，使得 成立的x的取值范围是_________． 三．解答题（共5小题，满分64分，18--20每小题12分，21,22每小题14分） 18．（2020·全国高三（文））已知函数 . （1）求 的单调区间； （2）求函数的极值；(要列表). 19.（2020·海南省直辖县级行政单位·临高二中高二月考）若 ， ，求： （1） 的单调增区间； （2） 在 上的最小值和最大值.20.（2020·北京通州区·高二期末）已知函数 . （1）求曲线 在点 ， 处的切线方程； （2）求 在 ， 上的最大值和最小值. 21．（2020·江苏宿迁市·宿豫中学高二月考）已知函数 , （1）计算函数 的导数 的表达式; （2）求函数 的值域. 22．（2020·哈尔滨市第十二中学校高二期末（文））已知函数 ， 是 的一个极值点． （1）求 的单调递增区间； （2）若当 时， 恒成立，求实数 的取值范围．