文档内容
期中检测卷 05
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间120分钟,试题共22题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题
目要求的.
1.设S 为等差数列{a}的前n项和,且a﹣a+a=6,则S =( )
n n 3 5 8 11
A.55 B.66 C.110 D.132
【答案】B
【分析】由已知利用等差数列的性质可求a=6,根据等差数列求和公式即可计算得解.
6
【解答】解:由a﹣a+a=6,得:a=6,
3 5 8 6
则 = = =66.
故选:B.
【知识点】等差数列的前n项和
2.已知曲线 在x=0处的切线l过点(﹣3,﹣a),则实数a等于( )
A.2 B.﹣2 C.3 D.﹣3
【答案】B
【分析】先根据f(x)求出f(0)和f'(x),然后求出切线l的斜率,再得到切线l的方程,根据切线l过
点(﹣3,﹣a),求出a的值.
【解答】解:由 ,得f(0)=﹣1,f'(x)= ,
∴切线l的斜率k=f'(0)=﹣1,∴切线l的方程为y+1=﹣x,即x+y+1=0,
∵切线l过点(﹣3,﹣a),∴﹣3﹣a+1=0,∴a=﹣2.
故选:B.
【知识点】利用导数研究曲线上某点切线方程
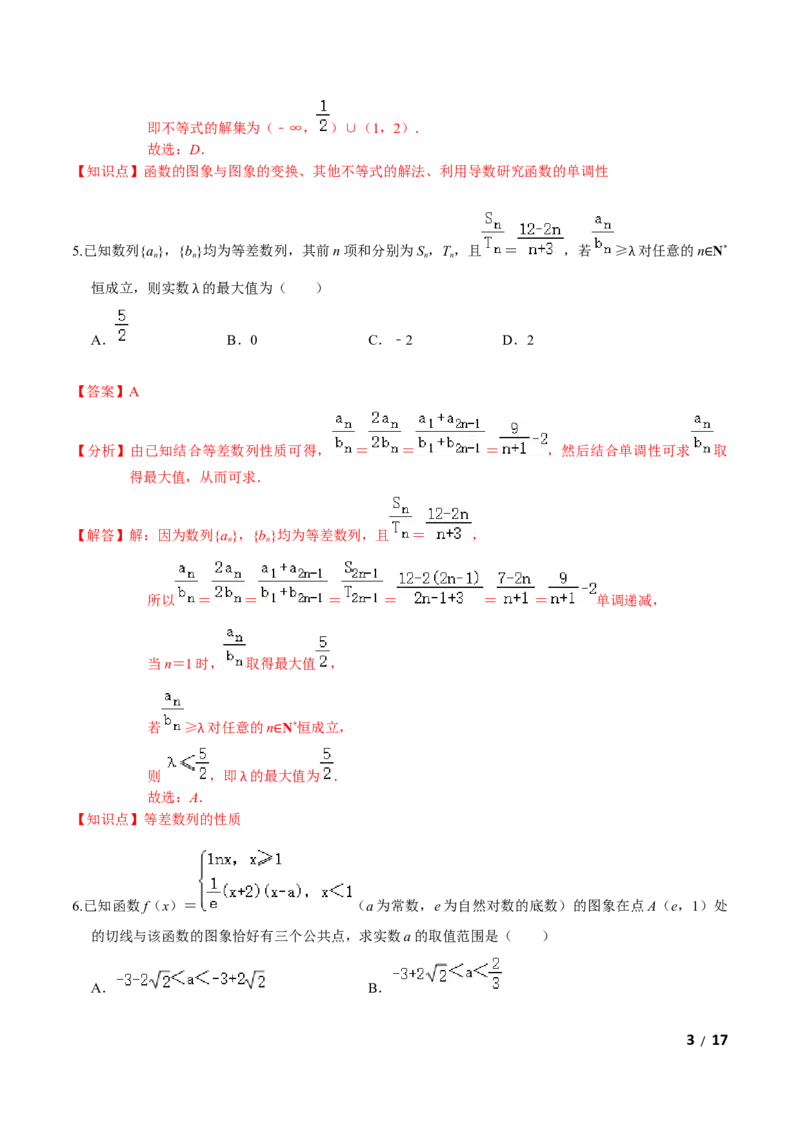
3.《算法统宗》是中国古代数学名著,由明代数学家程大位编著,它对我国民间普及珠算和数学知识起到
了很大的作用,是东方古代数学的名著,在这部著作中,许多数学问题都是以歌诀形式呈现的.“九儿
1 / 17问甲歌”就是其中一首:一个公公九个儿,若问生年总不知,自长排来差三岁,共年二百一十六,借问
大儿多少岁,各儿岁数要谁推.这位公公年龄最大的儿子年龄为( )
A.9岁 B.12岁 C.21岁 D.36岁
【答案】D
【分析】设第n个儿子的年龄为a ,则{a}是公差d=﹣3的等差数列,利用等差数列前n项和公式列出方
n n
程组,能求出结果.
【解答】解:设第n个儿子的年龄为a,则{a}是公差d=﹣3的等差数列,
n n
由题意得S=9a+ =216,
9 1
解得a=36.
1
故选:D.
【知识点】等差数列的前n项和
4.已知函数y=f(x)(x R)的图象如图所示,则不等式 <0的解集为( )
∈
A.(﹣∞,0)∪( ,2) B.(﹣1,1)∪(1,3)
C.(﹣∞, )∪( ,2) D.(﹣∞, )(1,2)
【答案】D
【分析】根据条件判断函数的单调性,利用数形结合即可解不等式.
【解答】解:∵ <0,即(x﹣1)•f′(x)<0,
∴不等式等价为x>1时,f′(x)<0,此时函数单调递减,由图象可知此时解集为:(1,
2).
当x<1时,f′(x)>0,此时函数单调递增,由图象可知x< ,
2 / 17即不等式的解集为(﹣∞, )∪(1,2).
故选:D.
【知识点】函数的图象与图象的变换、其他不等式的解法、利用导数研究函数的单调性
5.已知数列{a},{b}均为等差数列,其前n项和分别为S,T,且 = ,若 ≥ 对任意的n N*
n n n n
λ ∈
恒成立,则实数 的最大值为( )
λ
A. B.0 C.﹣2 D.2
【答案】A
【分析】由已知结合等差数列性质可得, = = = ,然后结合单调性可求 取
得最大值,从而可求.
【解答】解:因为数列{a},{b}均为等差数列,且 = ,
n n
所以 = = = = = = 单调递减,
当n=1时, 取得最大值 ,
若 ≥ 对任意的n N*恒成立,
λ ∈
则 ,即 的最大值为 .
故选:A.
λ
【知识点】等差数列的性质
6.已知函数f(x)= (a为常数,e为自然对数的底数)的图象在点A(e,1)处
的切线与该函数的图象恰好有三个公共点,求实数a的取值范围是( )
A. B.
3 / 17C. D.
【答案】C
【分析】求出原函数在点A(e,1)处的切线的方程,切线与该函数的图象恰好有三个公共点,只需求出
切线与当x<1时的函数联立方程组有两个交点,利用△>0求出a的范围,再讨论在x<1的这个
前提下成立,即在x<1时切线图象低于抛物线图象即可得答案;
【解答】解:函数f(x)在点A(e,1)处的切线的方程:由f(x)=lnx,x≥1,得f′(x)= ,则f′
(e)= ,
∴f(x)在点A(e,1)处的切线方程为y= x,①
函数y=f(x)= (x+2)(x﹣a),x<1 ②
∴由①②联立方程组可得: x<1
化简得:x2+(1﹣a)x﹣2a=0,③
∵切线与该函数的图象在A(e,1)点有一个交点,
∴只需要满足③在当x<1时有两个不相同的交点,利用△>0求出a的范围,
△>0即:a2+6a+1>0,
解得:a>﹣3+2 或 a<﹣3﹣2 ,④
在x<1时,切线图象应低于抛物线图象才能保证交于两不同的交点;
∴f(1)= (1+2)(1﹣a)> ×1
解得:a< ,⑤
∴④∩⑤得a的范围:
故选:C.
【知识点】利用导数研究曲线上某点切线方程
7.已知f(x)是定义在(﹣∞,0)∪(0,+∞)上的偶函数,当x (0,+∞)时,f(x)=| |.若a
∈
=f(﹣ ),b=f(﹣ ),c=f( ),则a,b,c的大小关系是( )
A.a>b>c B.c>b>a C.b>a>c D.c>a>b
【答案】D
4 / 17【分析】利用函数的奇偶性可得a=f( ),b=f( ),对函数f(x)求导,可得函数f(x)的单调性,
即可比较a,b,由对数的运算即可比较a,c,从而可得结论.
【解答】解:由题意,a=f(﹣ )=f( ),b=f(﹣ )=f( ),
当x (1,e)时,f(x)=| |= ,f′(x)= ,
∈
因为x (1,e),所以lnx<1,即f′(x)>0,
所以f(x)在(1,e)上单调递增,
∈
因为1< < <e,所以f( )<f( ),即b<a,
c=f( )=| |=﹣ ln = ln = ln ,a=f( )<f(2)=| |=
ln2,
因为 >2,所以c>a,即c>a>b.
故选:D.
【知识点】利用导数研究函数的单调性
8.已知等比数列{a}的前n项和为S ,若a+2a =0, ,且a≤S≤a+2,则实数a的取值范围是(
n n 1 2 n
)
A.[﹣1,0] B. C. D.[0,1]
【答案】B
【分析】设等比数列{a}的公比为q,由a+2a =0, ,可得a (1+2q)=0,a (1+q+q2)= ,联
n 1 2 1 1
立解出:a,q,利用求和公式及其单调性即可得出.
1
【解答】解:设等比数列{a}的公比为q,∵a+2a=0, ,
n 1 2
∴a(1+2q)=0,a(1+q+q2)= ,
1 1
解得:a=1,q=﹣ ,
1
∴S= = .
n
5 / 17当n=1时,S 取最大值1,当n=2时,S 取最小值 ,
n n
∴ ,﹣1≤a ,
故选:B.
【知识点】等比数列的前n项和
二、多选题(本大题共4小题,每小题5分,共20分)在每小题所给出的四个选项中,有多项是符合题目
要求的;错选或多选不得分。
9.已知函数f(x)的定义域为R且导函数为f'(x),如图是函数y=xf'(x)的图象,则下列说法正确的是
( )
A.函数f(x)的增区间是(﹣2,0),(2,+∞)
B.函数f(x)的增区间是(﹣∞,﹣2),(2,+∞)
C.x=﹣2是函数的极小值点
D.x=2是函数的极小值点
【答案】BD
【分析】根据题意,由函数y=xf′(x)的图象分析导函数的符号,进而可得f(x)的单调区间以及单调
性,据此分析可得答案.
【解答】解:根据题意,由函数y=xf′(x)的图象可知:
当x<﹣2时,xf′(x)<0,f′(x)>0,此时f(x)为增函数,
当﹣2<x<0时,xf′(x)>0,f′(x)<0,此时f(x)为减函数,
当0<x<2时,xf′(x)<0,f′(x)<0,此时f(x)为减函数,
当x>2时,xf′(x)>0,f′(x)>0,此时f(x)为增函数;
据此分析选项:函数f(x)的增区间是(﹣∞,﹣2),(2,+∞),则B正确,A错误;
x=﹣2是函数的极大值点,x=2是函数的极小值点,则D正确,C错误;
故选:BD.
【知识点】导数及其几何意义
6 / 1710.在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,如此
六日过其关.则下列说法正确的是( )
A.此人第二天走了九十六里路
B.此人第一天走的路程比后五天走的路程多六里
C.此人第三天走的路程占全程的
D.此人后三天共走了42里路
【答案】ABD
【分析】设此人第n天走a 里路,则{a}是首项为a ,公比为q= 的等比数列,由S =378求得首项,然
n n 1 6
后逐一分析四个选项得答案.
【解答】解:设此人第n天走a 里路,则{a}是首项为a,公比为q= 的等比数列,
n n 1
由等比数列前n项和公式得S= ,解得a=192,
6 1
在A中,a= =96,∴此人第二天走了九十六里路,故A正确;
2
在B中,378﹣192=186,192﹣186=6,∴此人第一天走的路程比后五天走的路程多六里,故
B正确;
在C中,a=192× =48, > ,故C错误;
3
在D中,a+a+a=192×( )=42,故D正确.
4 5 6
故选:ABD.
【知识点】等比数列的前n项和
11.等比数列{a}中,公比为q,其前n项积为T,并且满足a>1.a •a ﹣1>0, <0,下列选项
n n 1 99 100
中,正确的结论有( )
A.0<q<1
B.a •a ﹣1<0
99 101
C.T 的值是T 中最大的
100 n
D.使T>1成立的最大自然数n等于198
n
7 / 17【答案】ABD
【分析】由已知a a ﹣1>0,得q>0,再由 <0得到q<1说明A正确;再由等比数列的性质结
99 100
合a <1说明B正确;由T =T •a ,而0<a <1,求得 T <T ,说明C错误;分别求得
100 100 99 100 100 100 99
T >1,T <1说明D正确.
198 199
【解答】解:对于A,∵a a ﹣1>0,∴a2•q197>1,∴(a•q98)2•q>1.
99 100 1 1
∵a>1,∴q>0.
1
又∵ <0,∴a >1,且a <1.
99 100
∴0<q<1,故A正确;
对于B,∵ ,∴0<a •a <1,即 a •a ﹣1<0,故B正确;
99 101 99 101
对于C,由于T =T •a ,而0<a <1,故有 T <T ,故C错误;
100 99 100 100 100 99
对于D,T =a•a…a =(a•a )(a•a )…(a •a )=(a •a )×99>1,
198 1 2 198 1 198 2 197 99 100 99 100
T =a•a…a =(a•a )(a•a )…(a •a )•a <1,故D正确.
199 1 2 199 1 199 2 198 99 101 100
∴不正确的是C.
故选:ABD.
【知识点】等比数列的前n项和
12.已知函数f(x)=ex﹣alnx的定义域是D,有下列四个命题,其中正确的有( )
A.对于∀a (﹣∞,0),函数f(x)在D上是单调增函数
B.对于∀a∈(0,+∞),函数f(x)存在最小值
C.存在a (∈ ﹣∞,0),使得对于任意x D,都有f(x)>0成立
D.存在a∈(0,+∞),使得函数f(x)有∈两个零点
∈
【答案】ABD
【分析】先求导数,若为减函数则导数恒小于零;在开区间上,若有最小值则有唯一的极小值,若有零点
则对应方程有根.
【解答】解:由对数函数知:函数的定义域为:(0,+∞),f′(x)=ex﹣ ,
对于A:∵a (﹣∞,0)∴f′(x)=ex﹣ ≥0,是增函数.所以A正确,
∈
对于B:∵a (0,+∞),∴存在x有f′(x)=ex﹣ =0,可以判断函数有最小值,B正确.
对于C:画出函数y=ex,y=﹣alnx的图象,
∈
8 / 17如图:显然不正确.
对于D:令函数y=ex是增函数,y=alnx是增函数,
所以存在a (0,+∞),f(x)=ex﹣alnx=0有两个根,正确.
故选:ABD.
∈
【知识点】利用导数研究函数的单调性
三、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
13.记S 为等差数列{a}的前n项和.已知a=0,S=48,则公差d= .
n n 3 8
【答案】4
【分析】结合已知及等差数列的通项公式及求和公式及可求解公差d.
【解答】解:由已知可得, ,
解可得,d=4.
故答案为:4
【知识点】等差数列的前n项和
14.已知函数f(x)=ex(x+ ﹣a﹣1),其导函数为f'(x),若存在x [2,4]使得f(x)+xf′(x)>
0成立,则实数a的取值范围是 ﹣∞ . ∈
【答案】(-∞,6)
【分析】构造函数g(x)=xf(x),然后结合已知可判断其符号,结合二次不等式的性质即可求解.
【解答】解:令g(x)=xf(x)=ex[x2+(2a﹣1)﹣(a+1)x],
则存在x [2,4]使g′(x)=f(x)+xf′(x)>0,
即ex[x2﹣(a﹣1)x+a﹣2]>0在x [2,4]上有解,
∈
∈
9 / 17∴x2﹣(a﹣1)x+a﹣2=(x﹣1)[x﹣(a﹣2)]>0x [2,4]上有解,
结合二次不等式的性质可知,a﹣2≤1或1<a﹣2<4,
∈
解可得,a≤3或3<a<6,即a<6.
综上可得,a的范围(﹣∞,6).
故答案为:(﹣∞,6).
【知识点】利用导数研究函数的单调性
15.已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,
f(4)=1,则不等式f(x)<ex的解集为 .
【答案】(0,+∞)
【分析】令 ,利用导数和已知即可得出其单调性.再利用函数的奇偶性和已知可得g(0)=
1,即可得出.
【解答】解:令 ,
则 = ,
∵f′(x)<f(x),∴g′(x)<0.
∴g(x)在R上单调递减.
∵函数f(x+2)是偶函数,
∴函数f(﹣x+2)=f(x+2),
∴函数关于x=2对称,
∴f(0)=f(4)=1,
原不等式等价为g(x)<1,
∵g(0)= =1.
∴g(x)<1 g(x)<g(0),
∵g(x)在R上单调递减,
⇔
∴x>0.
∴不等式f(x)<ex的解集为(0,+∞).
故答案为:(0,+∞).
【知识点】导数的运算、函数单调性的性质与判断
16.设n N*,用A 表示所有形如 + +…+ 的正整数集合,其中0≤r <r <…<r≤n,且r N
n 1 2 n i
∈ ∈
(i N*),b 为集合A 中的所有元素之和.则{b}的通项公式为b= ﹣ .
n n n n
∈
10 / 17【答案】n•(2n+1-1)
【分析】把集合A 中每个数都表示为2的0到n的指数幂相加的形式,并确定20、21、22、…、2n每个数都
n
出现n次,于是利用等比数列求和公式计算 ,可求出数列{b}的通
n
项公式.
【解答】解:由题意可知,r、r、…、r 是0、1、2、…、n的一个排列,
1 2 n
且集合A 中共有n+1个数,若把集合A 中每个数表示为 + +…+ 的形式,
n n
则20、21、22、…、2n每个数都出现n次,
因此, = ,
故答案为:n•(2n+1﹣1).
【知识点】等比数列的前n项和
四、解答题(本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程
或演算步骤)
17.已知a为实数,函数f(x)=x3+ax3+x+a,若f'(﹣1)=0.
(1)求a的值.
(2)求函数y=f(x)在 上的极值.
【分析】(1)求导代入解方程;
(2)求出导函数后,采用表格法可求出极大极小值.
【解答】解:(1)f'(x)=3x2+2ax+1,∴f'(﹣1)=4﹣2a=0得a=2.
(2)由(1)知a=2∴f(x)=x3+2x2+x+2∴f'(x)=3x2+4x+1
=(3x+1)(x+1)令f'(x)=0得x=﹣1,
1
当x变化时f'(x),f(x)的变化情况如下表:
x ﹣1
(﹣ ,﹣1)
f'(x) + 0 ﹣ 0 +
f(x) ↑ 极大值 ↓ 极小值 ↑
由上表可知f (x)=f(﹣1)=2; .
极大值
故函数y=f(x)在[﹣ ,1]上的极大值为2,极小值为 .
11 / 17【知识点】导数的运算、利用导数研究函数的极值
18.已知函数f(x)= ,数列{a}满足a=f(1),a =f(a).
n 1 n+1 n
(1)求证:数列{ ﹣ }是等比数列;
(2)不等式 + +…+ ≥t+ ,n N*恒成立,求实数t的取值范围.
∈
【分析】(1)由题意可得可得a= ,a = ,取倒数减去 ,结合等比数列的定义,即可得证;
1 n+1
(2)求得 =2n﹣1+ ,运用等比数列的求和公式,化简可得 t≤2n﹣1恒成立,求得右边数
列的最小值,即可得到t的范围.
【解答】解:(1)证明:由函数f(x)= ,数列{a}满足a=f(1),a =f(a),
n 1 n+1 n
可得a= ,a = ,
1 n+1
﹣ = ﹣ = ( ﹣ ),
则数列{ ﹣ }是首项为 ,公比为 的等比数列;
(2)由(1)可得 ﹣ = •( )n﹣1=( )n+1,
即有 =2n﹣1+ ,
不等式 + +…+ ≥t+ ,即为
(1+2+…+2n﹣1)+( + +…+ )≥t+ ,
12 / 17即有 + ≥t+ ,
即为t≤2n﹣1恒成立,
由2n﹣1递增,可得2n﹣1的最小值为1,
则实数t的取值范围为(﹣∞,1].
【知识点】等比数列的性质、数列与不等式的综合
19.已知数列{a}的前n项和 ,且a,a,a 成等比数列.
n 2 4 8
(1)求数列{a}的通项公式;
n
(2)设 ,求数列{b}的前n项和T.
n n
【分析】(1)利用数列的前n项和推出数列的通项公式.
(2)利用裂项相消法求解数列的和即可.
【解答】解:(1)当n=1时,a=S=1+p,
1 1
当n≥2时, ,
经检验,n=1时也满足上式,所以a=2n﹣1+p.
n
因为a,a,a 成等比数列,
2 4 8
所以 ,
即(3+p)(15+p)=(7+p)2,解得p=1.
所以a=2n.
n
(2)由(1)及题设得, ,
所以T=b+b+…+b=
n 1 2 n
= = .
【知识点】等比数列的前n项和、数列的求和
20.已知函数f(x)=lnx﹣ax2+(2﹣a)x.
(1)若f′(1)=﹣6,求函数f(x)在(1,f(1))处的切线;
(2)设a>0,证明:当0<x< 时,f( +x)>f( ﹣x);
(3)若函数f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x,证明:f′(x)<0.
0 0
13 / 17【分析】(1)求出函数的导数,求得切线的斜率和切点,由点斜式方程可得切线的方程;
(2)设函数g(x)=f( +x)﹣f( ﹣x),则g(x)=ln(1+ax)﹣ln(1﹣ax)﹣2ax,求
出导数,判断单调性,即可得证;
(3)设出函数y=f(x)的图象与x轴交于A,B两点的横坐标,根据(2)的结论,和函数f
(x)的单调性,即可证明结论.
【解答】解:(1)函数f(x)的定义域为(0,+∞),
∵f(x)=lnx﹣ax2+(2﹣a)x,
∴f'(x)= ﹣2ax+2﹣a= =﹣ .
f′(﹣1)=a+1=﹣6,解得a=﹣7,
则函数f(x)在(1,f(1))处的切线斜率为k=﹣6,
切点为(1,16),
则所求切线的方程为y﹣16=﹣6(x﹣1),
即为6x+y﹣22=0;
(2)证明:设函数g(x)=f( +x)﹣f( ﹣x),
则g(x)=ln(1+ax)﹣ln(1﹣ax)﹣2ax,
g′(x)= + ﹣2a= ,
当x (0, )时,g′(x)>0,g(x)递增,
而g(0)=0,即有g(x)>0,
∈
故当0<x< 时,f( +x)>f( ﹣x).
(3)证明:当a≤0时,f′(x)>0恒 成立,因此f(x)在(0,+∞)单调递增,
即有函数y=f(x)的图象与x轴至多有一个交点,
故a>0,从而f(x)的最大值为f( ),且f( )>0,
不妨设A(x,0),B(x,0),0<x<x,
1 2 1 2
则0<x< <x,
1 2
由(2)得,f( ﹣x)=f( + ﹣x)>f(x)=f(x)=0,
1 1 1 2
又f(x)在( ,+∞)单调递减,
∴ ﹣x<x,于是x= ,
1 2 0
14 / 17当x ( ,+∞)(a>0)时,f′(x)<0,
则f′( x)<0成立.
∈ 0
【知识点】利用导数研究曲线上某点切线方程、利用导数研究函数的单调性
21.已知函数f(x)=axex(a R,a≠0),g(x)=x+lnx+1.
(I)讨论f(x)的单调性;∈
(II)若对任意的x>0,f(x)≥g(x)恒成立,求实数a的取值范围.
【分析】(I)先对函数求导,然后结合导数与单调性关系对a进行分类讨论可求;
(II)由已知不等式分离参数后转化为求解函数的值域,结合导数及函数性质可求;
(法二:)结合重要不等式ex≥x+1,及已知不等式特点进行合理辅值可证明.
【解答】解:(I)f′(x)=a(x+1)ex,a≠0,
当a>0时,易得x (﹣∞,﹣1)时,f′(x)<0,函数单调递减,当x (﹣1,+∞)时,
f′(x)>0,函数单调递增,
∈ ∈
当a<0时,易得x (﹣∞,﹣1)时,f′(x)>0,函数单调递增,当x (﹣1,+∞)时,
f′(x)<0,函数单调递减,
∈ ∈
(II)由f(x)≥g(x)代入可得,a ,x>0,
令 F(x)= ,x>0,
则 ,
令t(x)=x+lnx,x>0,则t′(x)=1+ >0,
即t(x)在(0,+∞)上单调递增,且t( )= ,t(1)=1>0,
故存在 使得t(x)=x+lnx =0,
0 0 0
从而有F(x)在(0,x)单调递增,在(x,+∞)上单调递减,
0 0
故F(x) =F(x)= =1,
max 0
故a≥1.
法二:令h(x)=ex﹣x﹣1,则h′(x)=ex﹣1,
易得,当x>0时,h′(x)>0,函数单调递增,当x<0时,h′(x)<0,函数单调递减,
故当x=0时,h(x)取得最小值h(0)=0,即ex≥x+1,x=0时取等号,
故xex=ex+lnx≥x+lnx+1,当x+lnx=0时取等号,
所以当a≥1时,axex≥xex≥x+lnx+1恒成立.
15 / 17综上a≥1.
【知识点】利用导数研究函数的最值、利用导数研究函数的单调性
22.已知数列{a}满足a+a=12,a=6, 为 与 的等差中项.
n 1 3 2
(1)求数列{a}的通项公式;
n
(2)若数列{a}的前n项和为S ,数列{b}满足b =2S﹣a﹣1,b +b = a (a+2),求证:
n n n 2n﹣1 n n 2n 2n﹣1 n n
+…+ (n≥2).
【分析】(1)根据等差中项的概念得到数列{a}的奇数项和偶数项分别成公差为8的等差数列,再分奇偶
n
分别求出数列{a}的通项公式,即可得到结果;
n
(2)先根据等差数列的求和公式求出 S ,并根据题意求出数列{b}的通项公式,再利用数学
n n
归纳法证明不等式即可.
【解答】(1)解:∵ 为 与 的等差中项,∴ = + ,整理得:a ﹣a =
n+2 n
8,
∴a﹣a=8,又a+a=12,可解得:a=2,
3 1 1 3 1
∴数列{a}中所有的奇数项是以a=2为首项,公差为8的等差数列,
n 1
∴a =2+8(n﹣1)=8n﹣6=4(2n﹣1)﹣2,
2n﹣1
又∵a=6,∴数列{a}中所有的偶数项是以a=6为首项,公差为8的等差数列,
2 n 2
∴a =6+8(n﹣1)=8n﹣2=4×2n﹣2,
2n
综上,a=4n﹣2;
n
(2)证明:由(1)可得:S= =2n2,
n
∴b =2S﹣a﹣1=4n2﹣4n+1=(2n﹣1)2,
2n﹣1 n n
∴当n为奇数时,b=n2,
n
又∵b +b = a(a+2),
2n 2n﹣1 n n
∴b =4n(2n﹣1)﹣b =4n(2n﹣1)﹣(2n﹣1)2=(2n)2﹣1,
2n 2n﹣1
∴当n为偶数时,b=n2﹣1,
n
∴b= ,
n
①当n=2时,左边=1+ = ,右边= ,不等式成立;
16 / 17②假设当n=k(k≥2)时,不等式成立,即 + +…+ ≥ ﹣ ,
∵ ≥ ,
∴当n=k+1时, + +…+ + ≥ ﹣ + ,
要证当n=k+1时不等式成立,只需证 ﹣ ≥﹣ 即可,
只需证 ≥ ﹣ ,
只需证 ≥ ,
只需证k+1≤k+2,这显然成立,
故当n=k+1时不等式也成立,
综上, +…+ (n≥2).
【知识点】等差数列的性质、数列递推式
17 / 17