2001年福建高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_福建

2001 年福建高考理科数学真题及答案 本试卷分第I卷（选择题）和第II卷（非选择题）两部分。第I卷1至2页。第II 卷3至9页。共150分。考试时间120分钟。 第I卷（选择题 60分） 注意事项： 1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写 在答题卡上。 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需 改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。 3．考试结束，监考人将本试卷和答题卡一并收回。 参考公式： 三角函数的积化和差公式 1 sincos  sinsin 2 1 cossin  sinsin 2 1 coscos  cos   cos   2 1 sinsin   coscos 2 正棱台、圆台的侧面积公式 1 S  ccl 台侧 2 其中c、c分别表示上、下底面周长，l 表示斜高或母线长 台体的体积公式 1  V  S SS S h 台体 3 其中S、S 分别表示上、下底面积，h表示高 一、 选择题：本大题共12小题；第每小题5分，共60分。在每小题给出的 四个选项中，只有一项是符合题目要求的。 （1） 若sincos0，则在 （A）第一、二象限 （B）第一、三象限 （C）第一、四象限 （D）第二、四象限 （2）过点A  1,1 、B  1,1  且圆心在直线x y20上的圆的方程是 （A）  x3 2   y1 2  4 （B）  x3 2   y1 2  4 （C）  x1 2   y1 2  4 （D）  x1 2   y1 2  4   （3）设 a 是递增等差数列，前三项的和为12，前三项的积为48，则它的首项是 n （A）1 （B）2 （C）4 （D）6 第1页 | 共11页（4）若定义在区间  1，0  内的函数 f  x  log  x1  满足 f(x) 0，则a的取值范围是 2a 1 1 1 （A）（0， ） （B）（0， ] （C）（ ，+） （D）（0，+） 2 2 2  (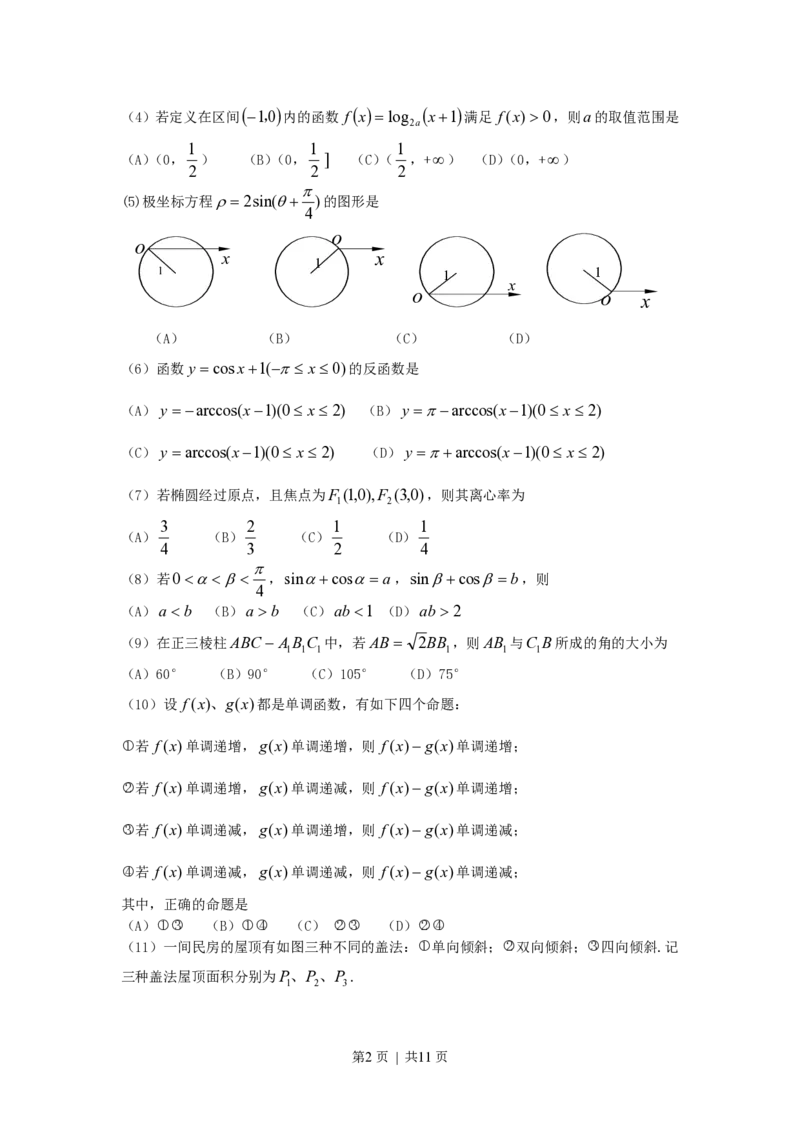5)极坐标方程 2sin( )的图形是 4 o o x x 1 1 1 1 x o o x （A） （B） （C） （D） （6）函数y cosx1( x 0)的反函数是 （A）y  arccos(x1)(0 x  2) （B）y arccos(x1)(0 x  2) （C）y arccos(x1)(0 x  2) （D）y arccos(x1)(0 x  2) （7）若椭圆经过原点，且焦点为F (1,0),F (3,0)，则其离心率为 1 2 3 2 1 1 （A） （B） （C） （D） 4 3 2 4  （8）若0 ，sincos a，sincosb，则 4 （A）a b （B）a b （C）ab1 （D）ab  2 （9）在正三棱柱ABC  A BC 中，若AB  2BB ，则AB 与C B所成的角的大小为 1 1 1 1 1 1 （A）60° （B）90° （C）105° （D）75° （10）设 f(x)、g(x)都是单调函数，有如下四个命题： ○1若 f(x)单调递增，g(x)单调递增，则 f(x)g(x)单调递增； ○2若 f(x)单调递增，g(x)单调递减，则 f(x)g(x)单调递增； ○3若 f(x)单调递减，g(x)单调递增，则 f(x)g(x)单调递减； ○4若 f(x)单调递减，g(x)单调递减，则 f(x)g(x)单调递减； 其中，正确的命题是 （A）○1○3 （B）○1○4 （C） ○2○3 （D）○2○4 （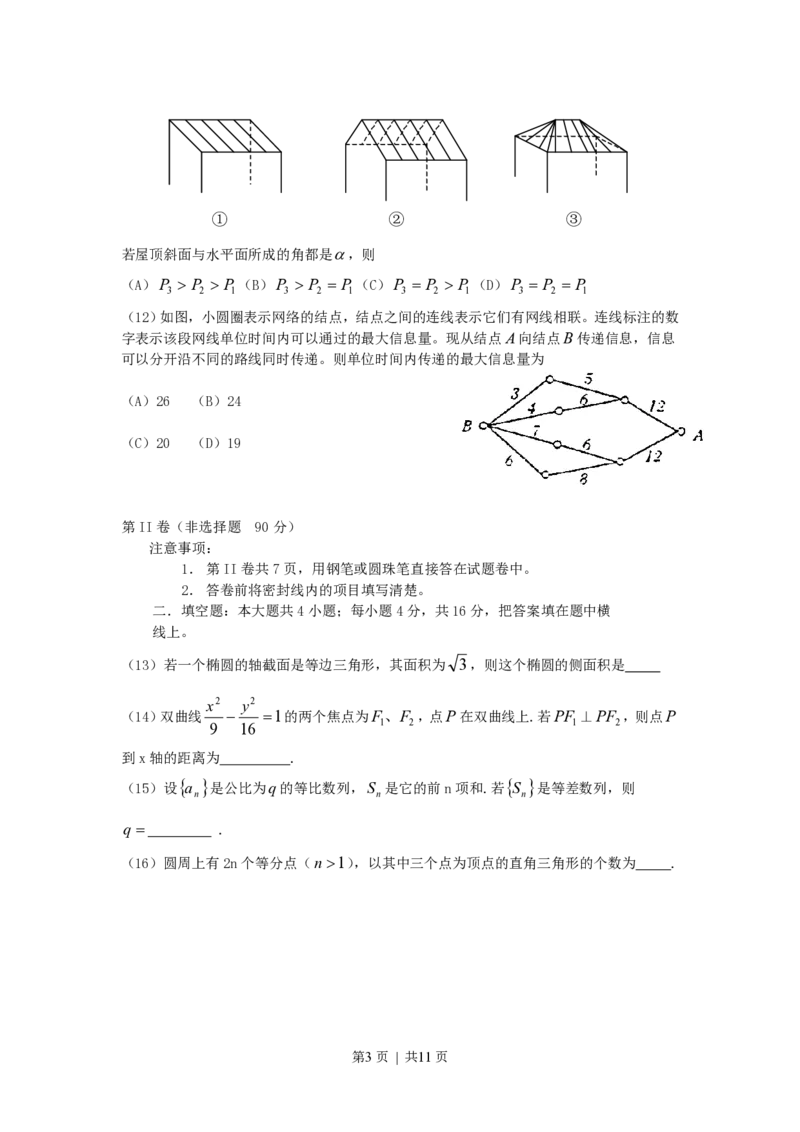11）一间民房的屋顶有如图三种不同的盖法：○1单向倾斜；○2双向倾斜；○3四向倾斜.记 三种盖法屋顶面积分别为P、P、P . 1 2 3 第2页 | 共11页① ② ③ 若屋顶斜面与水平面所成的角都是，则 （A）P  P  P （B）P  P  P （C）P  P  P （D）P  P  P 3 2 1 3 2 1 3 2 1 3 2 1 （12）如图，小圆圈表示网络的结点，结点之间的连线表示它们有网线相联。连线标注的数 字表示该段网线单位时间内可以通过的最大信息量。现从结点A向结点B传递信息，信息 可以分开沿不同的路线同时传递。则单位时间内传递的最大信息量为 （A）26 （B）24 （C）20 （D）19 第II卷（非选择题 90分） 注意事项： 1．第II卷共7页，用钢笔或圆珠笔直接答在试题卷中。 2．答卷前将密封线内的项目填写清楚。 二．填空题：本大题共4小题；每小题4分，共16分，把答案填在题中横 线上。 （13）若一个椭圆的轴截面是等边三角形，其面积为 3，则这个椭圆的侧面积是 x2 y2 （14）双曲线  1的两个焦点为F、F ，点P在双曲线上.若PF ⊥PF ，则点P 9 16 1 2 1 2 到x轴的距离为 .     （15）设 a 是公比为q的等比数列，S 是它的前n项和.若 S 是等差数列，则 n n n q  . （16）圆周上有2n个等分点（n 1），以其中三个点为顶点的直角三角形的个数为 . 第3页 | 共11页三、解答题：本大题共6小题；共74分，解答应写出文字说明、证明过程或 演算步骤。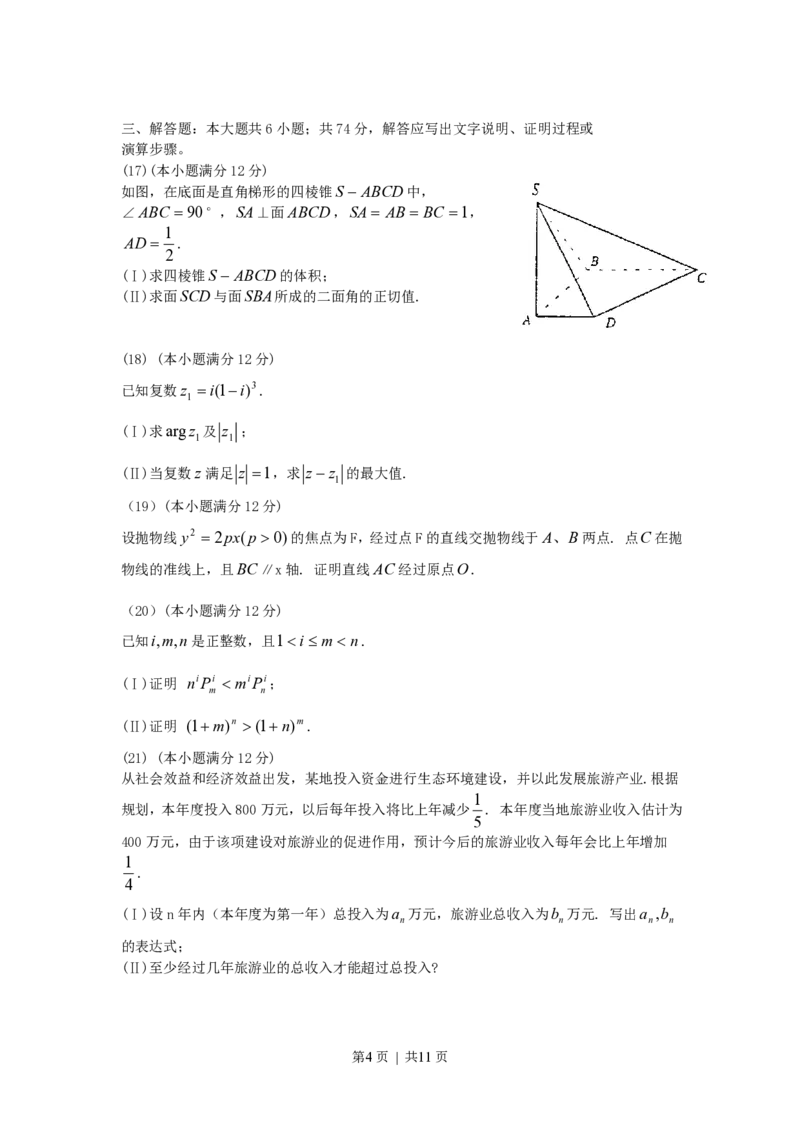 (17)(本小题满分12分) 如图，在底面是直角梯形的四棱锥S  ABCD中， ∠ABC 90°，SA⊥面ABCD，SA AB  BC 1， 1 AD  . 2 (Ⅰ)求四棱锥S  ABCD的体积； (Ⅱ)求面SCD与面SBA所成的二面角的正切值. (18) (本小题满分12分) 已知复数z i(1i)3. 1 (Ⅰ)求argz 及 z ； 1 1 (Ⅱ)当复数z满足 z 1，求 zz 的最大值. 1 （19）(本小题满分12分) 设抛物线y2  2px(p 0)的焦点为F，经过点F的直线交抛物线于A、B两点. 点C在抛 物线的准线上，且BC∥x轴. 证明直线AC经过原点O. （20）(本小题满分12分) 已知i,m,n是正整数，且1i  m n. (Ⅰ)证明 niPi  miPi； m n (Ⅱ)证明 (1m)n (1n)m. (21) (本小题满分12分) 从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业.根据 1 规划，本年度投入800万元，以后每年投入将比上年减少 . 本年度当地旅游业收入估计为 5 400万元，由于该项建设对旅游业的促进作用，预计今后的旅游业收入每年会比上年增加 1 . 4 (Ⅰ)设n年内（本年度为第一年）总投入为a 万元，旅游业总收入为b 万元. 写出a ,b n n n n 的表达式； (Ⅱ)至少经过几年旅游业的总收入才能超过总投入? 第4页 | 共11页(22) (本小题满分14分) 1 设 f(x)是定义在R上的偶函数，其图象关于直线x 1对称，对任意x ,x [0, ]，都有 1 2 2 f(x  x )  f(x ) f(x )，且 f(1)  a 0. 1 2 1 2 1 1 (Ⅰ)求 f( )及 f( ); 2 4 (Ⅱ)证明 f(x)是周期函数； 1 (Ⅲ)记a  f(2n )，求lim(lna ). n 2n n n 参考解答及评分标准 说明： 一. 本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如 果考生物解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则． 二. 对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的 内容和难度，可视影响的程度决定部分的给分，但不得超过该部分正确解答得分数的一半； 如果后继部分的解答有较严重的错误，就不再给分． 三. 解答右端所注分数，表示考生正确做到这一步应得的累加分数． 四. 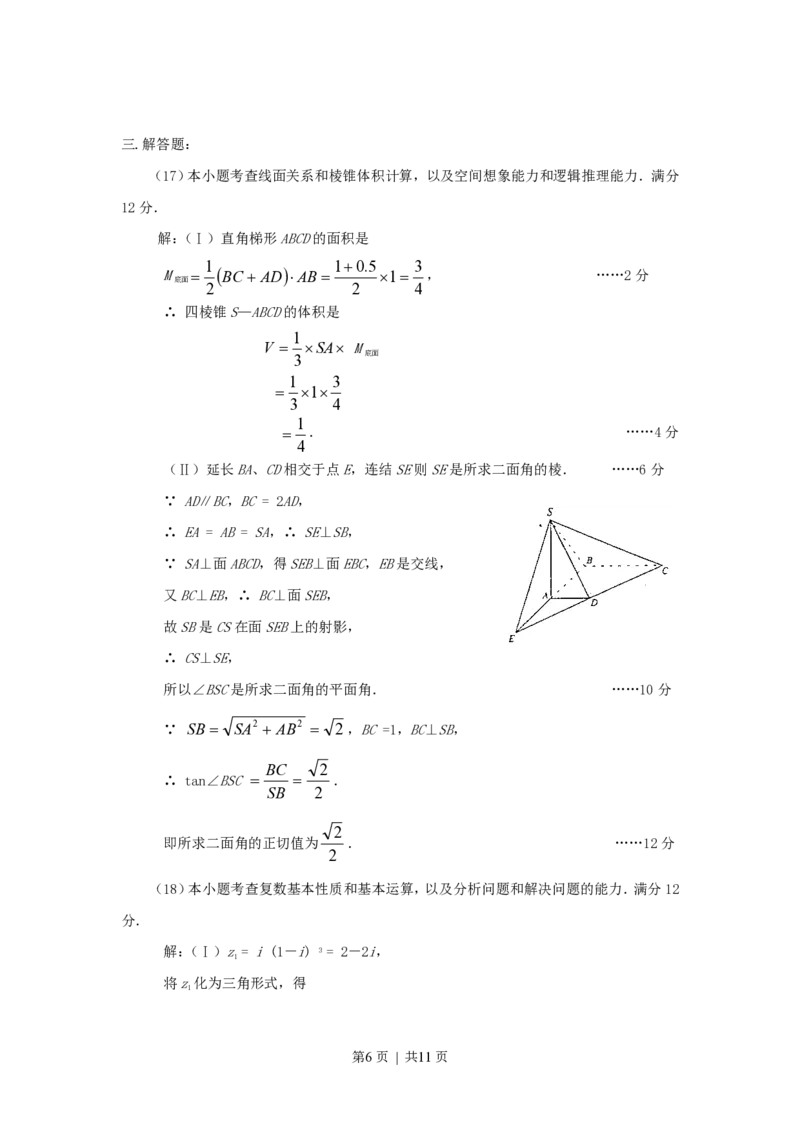只给整数分数．选择题和填空题不给中间分． 一.选择题：本题考查基本知识和基本运算．每小题5分，满分60分． （1）B （2）C （3）B （4）A （5）C （6）A （7）C （8）A （9）B （10）C （11）D （12）D 二.填空题：本题考查基本知识和基本运算．每小题4分，满分16分． 16 （13）2π （14） （15）1 （16）2n (n－1) 5 第5页 | 共11页三.解答题： （17）本小题考查线面关系和棱锥体积计算，以及空间想象能力和逻辑推理能力．满分 12分． 解：（Ⅰ）直角梯形ABCD的面积是 1 10.5 3 M   BC  AD  AB  1 ， ……2分 底面 2 2 4 ∴ 四棱锥S—ABCD的体积是 1 V  SA M 底面 3 1 3  1 3 4 1  ． ……4分 4 （Ⅱ）延长BA、CD相交于点E，连结SE则SE是所求二面角的棱． ……6分 ∵ AD∥BC，BC = 2AD， ∴ EA = AB = SA，∴ SE⊥SB， ∵ SA⊥面ABCD，得SEB⊥面EBC，EB是交线， 又BC⊥EB，∴ BC⊥面SEB， 故SB是CS在面SEB上的射影， ∴ CS⊥SE， 所以∠BSC是所求二面角的平面角． ……10分 ∵ SB  SA2  AB2  2 ，BC =1，BC⊥SB， BC 2 ∴ tan∠BSC   ． SB 2 2 即所求二面角的正切值为 ． ……12分 2 （18）本小题考查复数基本性质和基本运算，以及分析问题和解决问题的能力．满分12 分． 解：（Ⅰ）z= i (1－i) 3 = 2－2i， 1 将z化为三角形式，得 1 第6页 | 共11页 7 7 z  2 2cos isin ， 1  4 4  7 ∴ argz  ， z  2 2． ……6分 1 4 1 （Ⅱ）设z= cos α＋i sin α，则 z－z= ( cos α－2)＋(sin α＋2) i， 1 zz 2   cos2 2   sin2 2 1  94 2sin( )， ……9分 4  2 当sin( ) = 1时， zz 取得最大值94 2． 4 1 从而得到 zz 的最大值为2 2 1． ……12分 1 （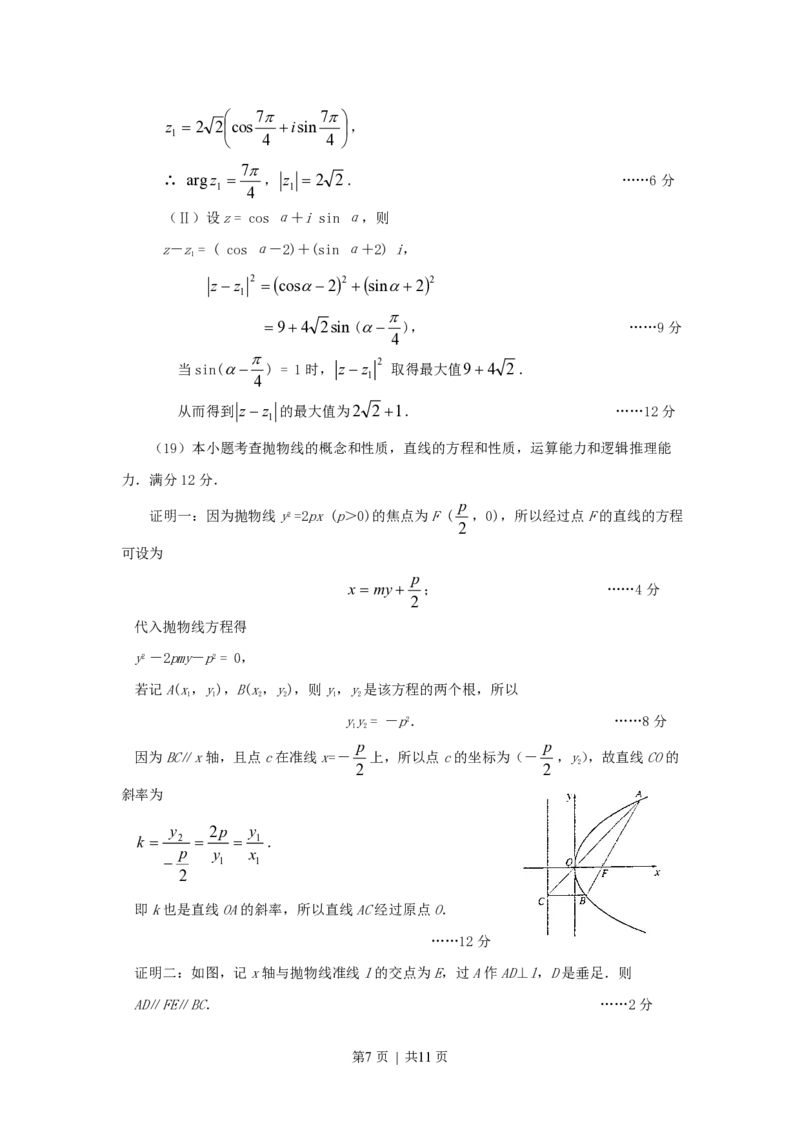19）本小题考查抛物线的概念和性质，直线的方程和性质，运算能力和逻辑推理能 力．满分12分． p 证明一：因为抛物线y2 =2px (p＞0)的焦点为F ( ，0)，所以经过点F的直线的方程 2 可设为 p x  my ； ……4分 2 代入抛物线方程得 y2 －2pmy－p2 = 0， 若记A(x，y)，B(x，y)，则y，y是该方程的两个根，所以 1 1 2 2 1 2 yy= －p2． ……8分 1 2 p p 因为BC∥x轴，且点c在准线x= － 上，所以点c的坐标为（－ ，y），故直线CO的 2 2 2 斜率为 y 2p y k  2   1 ． p y x  1 1 2 即k也是直线OA的斜率，所以直线AC经过原点O． ……12分 证明二：如图，记x轴与抛物线准线l的交点为E，过A作AD⊥l，D是垂足．则 AD∥FE∥BC． ……2分 第7页 | 共11页连结AC，与EF相交于点N，则 EN CN BF   ， AD AC AB NF AF  ， ……6分 BC AB 根据抛物线的几何性质， AF  AD ， BF  BC ， ……8分 AD  BF AF  BC ∴ EN    NF ， AB AB 即点N是EF的中点，与抛物线的顶点O重合，所以直线AC经过原点O． ……12分 （20）本小题考查排列、组合、二项式定理、不等式的基本知识和逻辑推理能力．满分 12分． （Ⅰ）证明： 对于1＜i≤m有 pi = m·…·(m－i＋1)， m pi m m1 mi1 m   … ， mi m m m pi n n1 ni1 同理 n   … ， ……4分 ni n n n nk mk 由于 m＜n，对整数k = 1，2…，i－1，有  ， n m pi pi 所以 n  m ，即mipi  nipi ． ……6分 ni mi n m （Ⅱ）证明由二项式定理有 n  1m n  miCi ， n i0 m  1n m  niCi ， ……8分 m i0 由 (Ⅰ)知mipi ＞nipi (1＜i≤m＜n＝， n m 第8页 | 共11页pi pi 而 Ci  m ，Ci  n ， ……10分 m i! n i! 所以， miCi  niCi (1＜i≤m＜n＝． n m m m 因此，miCi  niCi ． n m i2 i2 又 m0C0  n0C0 1，mC1  nC1  mn，miCi 0  mi  n  ． n m n m n n m ∴ miCi  niCi ． n m i0 i0 即 (1＋m)n＞(1＋n)m． ……12分 （21）本小题主要考查建立函数关系式、数列求和、不等式等基础知识；考查综合运用 数学知识解决实际问题的能力．满分12分． 1 解：（Ⅰ）第1年投入为800万元，第2年投入为800×（1－ ）万元，……，第n年 5 1 投入为800×（1－ ）n－1万元． 5 所以，n年内的总投入为 1 1 a= 800＋800×（1－ ）＋…＋800×（1－ ）n－1 n 5 5 n 1  800(1 )k1 5 k1 4 = 4000×[1－( )n]； ……3分 5 1 第1年旅游业收入为400万元，第2年旅游业收入为400×（1＋ ）万元，……，第 4 1 n年旅游业收入为400×（1＋ ）n－1万元． 4 所以，n年内的旅游业总收入为 1 1 b= 400＋400×（1＋ ）＋…＋400×（1＋ ）n－1 n 4 4 n 5  400( )k1 4 k1 4 = 1600×[ ( )n－1]． ……6分 5 （Ⅱ）设至少经过n年旅游业的总收入才能超过总投入，由此 第9页 | 共11页b－a＞0， n n 5 4 即 1600×[（ ）n －1]－4000×[1－（ ）n]＞0． 4 5 4 4 化简得 5×（ ）n＋2×（ ）n －7＞0， ……9分 5 5 4 设x （ ）n，代入上式得 5 5x2－7x＋2＞0， 解此不等式，得 2 x  ，x＞1(舍去)． 5 4 2 即 （ ）n＜ ， 5 5 由此得 n≥5． 答：至少经过5年旅游业的总收入才能超过总投入． ……12分 （22）本小题主要考查函数的概念、图像，函数的奇偶性和周期性以及数列极限等基础 知识；考查运算能力和逻辑思维能力．满分14分． 1 （Ⅰ）解：因为对x，x∈[0， ]，都有f (x＋x) = f (x) · f (x)，所以 1 2 1 2 1 2 2 x x f(x) f ( ) · f ( )≥0，x∈[0，1]． 2 2 1 1 1 1 1 ∵ f(1) f (  ) = f ( ) · f ( ) = [f ( )]2， 2 2 2 2 2 1 1 1 1 1 f ( )f (  ) = f ( ) · f ( ) = [f 2 4 4 4 4 1 ( )]2． ……3分 4 f(1)  a 0， 1 1 1 1 ∴ f ( ) a2 ，f ( ) a4 ． ……6分 2 4 （Ⅱ）证明：依题设y = f (x)关于直线x = 1对称， 故 f (x) = f (1＋1－x)， 即f (x) = f (2－x)，x∈R． ……8分 又由f (x)是偶函数知f (－x) = f (x) ，x∈R， ∴ f (－x) = f (2－x) ，x∈R， 将上式中－x以x代换，得 第10页 | 共11页f (x) = f (x＋2)，x∈R． 这表明f (x)是R上的周期函数，且2是它的一个周期． ……10分 （Ⅲ）解：由（Ⅰ）知f (x)≥0，x∈[0，1]． 1 1 1 1 ∵ f ( )= f (n · ) = f ( ＋（n－1）· ) 2 2n 2n 2n 1 1 = f ( ) · f (（n－1）· ) 2n 2n 1 1 1 = f ( ) · f ( ) · … ·f ( ) 2n 2n 2n 1 = [ f ( )]n， 2n 1 1 f ( ) = a2， 2 1 1 ∴ f ( ) = a2n． 2n ∵ f (x)的一个周期是2， 1 1 1 ∴ f (2n＋ ) = f ( )，因此a= a2n， …… n 2n 2n 12分 1   ∴ lim lna  lim( lna) = 0． ……14分 n n n 2n 第11页 | 共11页