文档内容
更多全科试卷,请关注公众号:高中试卷君
2024 届高三二轮复习“8+3+3”小题强化训练(18)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.有8位同学一次数学测试的分数分别是:111,118,125,130,130,132,136,140,则这组数据
的75百分位数是( )
A.130 B.132 C.134 D.136
【答案】C
【解析】 , ,
故选:C
2.已知复数 ( 为虚数单位),则z的共轭复数 ( )
A. B. C. D.
【答案】A
【解析】
故
故选:A.
3.若向量 ,则“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】C
【解析】由题意 ,则“ ”是“ ”的充要条件.
故选:C.
4.若 ,则 ( )
A. B. C. D.
【答案】D
【解析】因为 ,
则 .
故选:D.
5.口袋里有红黄蓝绿的小球各四个,这些球除了颜色之外完全相同,现在从口袋里任意取出四个小
球,则不同的方法有( )种.
A. 48 B. 77 C. 35 D. 39
【答案】C
【解析】根据条件,取出的四个球可以分为一种,两种,三种,四种颜色,
当取出的球只有一种颜色时:有 种;
当取出的球只有二种颜色时:有 种;更多全科试卷,请关注公众号:高中试卷君
当取出的球只有三种颜色时:有 种;
当取出的球只有四种颜色时:有 种;
共有: 种.故C项正确.
故选:C.
6.科技是一个国家强盛之根,创新是一个民族进步之魂,科技创新铸就国之重器,极目一号(如图
1)是中国科学院空天信息研究院自主研发的系留浮空器.2022年5月,“极目一号”III型浮空艇成
功完成10次升空大气科学观测,最高升空至9050米,超过珠穆朗玛峰,创造了浮空艇大气科学观测
海拔最高的世界纪录,彰显了中国的实力.“极目一号”III型浮空艇长55米,高19米,若将它近似
看作一个半球、一个圆柱和一个圆台的组合体,正视图如图2所示,则“极目一号”III型浮空艇的体
积约为( )
(参考数据: , , , )
A. B. C. D.
【答案】A
【解析】由图2得半球、圆柱底面和圆台一个底面的半径为 (m),而圆台一个底面的半
径为 (m),
则 (m3),
(m3),
(m3),
所以 (m3).
故选:A.
7.已知点 为直线 上的动点,平面内的动点 到两定点 , 的距离
分别为 和 ,且 ,则点 和点 距离的最小值为( )
A. B. C. D.
【答案】
【解析】设 ,由 得 ,
即 ,即 ,更多全科试卷,请关注公众号:高中试卷君
也即 ,所以 点 轨迹是以 为圆心,半径为 的圆,
的
所以点 和点 距离的最小值为 .
故选:B
8.已知 , , ,则 , , 的大小关系是( )
A. B. C. D.
【答案】C
【解析】因为 , ,
构造函数 ,
因为 ,
所以当 时, ,函数 在 上单调递减,
当 时, ,函数 在 上单调递增,
又 ,所以 ,
故 ,即 ,更多全科试卷,请关注公众号:高中试卷君
因为 , ,
因为 , ,
所以 , ,
所以 ,即 ,
所以 ,
故选:C.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.关于函数 ,则下列命题正确的是( )
A. 的图象关于点 对称
B. 函数 的最小正周期为
C. 在区间 上单调递增
D. 将 图象上所有点的横坐标伸长为原来的2倍,再把图象向右平移 个单位长度得到的函数为
【答案】ACD
【解析】由于 ,所以 ,故 的图象
关于点 对称,A正确,
函数 的最小正周期为 ,故B错误,
当 时, ,故C正确,
将 图象上所有点的横坐标伸长为原来的2倍,得到 ,再把图象向右平移 个单
位长度得到的函数为 ,D正确,
故选:ACD
10.已知离散型随机变量 服从二项分布 ,其中 ,记 为奇数的概率为
, 为偶数的概率为 ,则下列说法中正确的有( )
A. B. 时,更多全科试卷,请关注公众号:高中试卷君
C. 时, 随着 的增大而增大 D. 时, 随着 的增大而减小
【答案】ABC
【解析】对于A选项,由概率的基本性质可知, ,
故A正确,
对于B选项,由 时,离散型随机变量 服从二项分布 ,
则 ,
所以 ,
,
所以 ,故B正确,
对于C,D选项, ,
当 时, 为正项且单调递增的数列,
故 随着 的增大而增大故选项C正确,
当 时, 为正负交替的摆动数列,
故选项D不正确.
故选:ABC.
11.在直四棱柱 中,所有棱长均2, ,P为 的中点,点Q在四边
形 内(包括边界)运动,下列结论中正确的是( )
A. 当点Q在线段 上运动时,四面体 的体积为定值
B. 若 平面 ,则AQ的最小值为更多全科试卷,请关注公众号:高中试卷君
C. 若 的外心为M,则 为定值2
D. 若 ,则点Q的轨迹长度为
【答案】ABD
【解析】对于A,因为 ,又因为 面 , 面 ,所以 面 ,
所以直线 到平面 的距离相等,又 的面积为定值,故A正确;
对于B,取 的中点分别为 ,连接 ,
则易证明: , 面 , 面 ,所以 面 ,
又因为 ,, 面 , 面 ,所以 面 ,
,所以平面 面 , 面 ,所以 平面
当 时,AQ有最小值,则易求出
,所以 重合,所以则
AQ的最小值为 ,故B正确;
对于C,若 的外心为M,,过 作 于点 ,
则 .故C错误;更多全科试卷,请关注公众号:高中试卷君
对于D,过 作 于点 ,易知 平面 ,
在 上取点 ,使得 ,则 ,
所以若 ,则 在以 为圆心,2为半径的圆弧 上运动,
又因为 所以 ,则圆弧 等于 ,故D正确.
故选:ABD.
三、填空题:本题共3小题,每小题5分,共15分.
12.已知集合 , ,若 ,则实数m的取值范围为
__________.
【答案】
【解析】由集合 中,当 时, ,当且仅当 ,即
时等号成立,
故 .因为 ,所以 ,所以 ,故实
数m的取值范围为 .
故答案为: .
13.已知函数 为奇函数, 为偶函数,且当 时, ,则
______.
【答案】1更多全科试卷,请关注公众号:高中试卷君
【解析】由函数 为奇函数, 为偶函数,
则 , 为偶函数,
所以 得图象关于 对称,且关于 对称,
即 , ,
则 ,
所以 ,即函数 的周期为4,
则 .
故答案为:1.
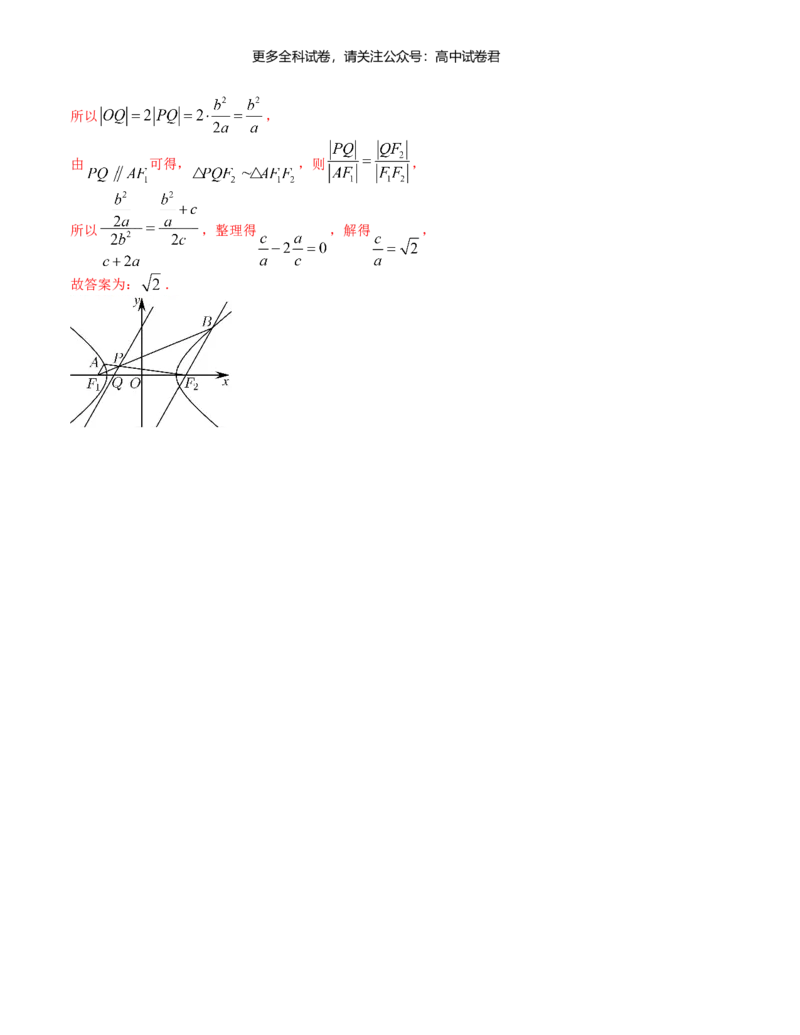
14.已知双曲线 : 的左右焦点分别为 , , 为坐标原点, , 为 上位于 轴
上方的两点,且 , .记 , 交点为 ,过点 作 ,交 轴于
点 .若 ,则双曲线 的离心率是______.
【答案】
【解析】做出图像,如图所示,则 ,
在 中,由 得, ,
设 ,则 ,
所以 ,解得 ,即 ,
在 中,由 得, ,
设 ,则 ,
所以 ,解得 ,即 ,
因为 ,
所以 ,
则 ,即 ,
所以 ,解得 ,更多全科试卷,请关注公众号:高中试卷君
所以 ,
由 可得, ,则 ,
所以 ,整理得 ,解得 ,
故答案为: .