文档内容
格致课堂
6.4.1 平面几何中的向量方法
一、选择题
1.在四边形ABCD中,若 ,且| |=| |,则这个四边形是( )
A.平行四边形 B.矩形
C.等腰梯形 D.菱形
【答案】C
【解析】
由 知DC∥AB,且|DC|= |AB|,因此四边形ABCD是梯形.又因为| |=| |,所以四边
形ABCD是等腰梯形.故选C
2.(2020·全国高一课时练习)已知 是 所在平面内一点,且满足
,则 为
A.等腰三角形 B.直角三角形 C.等边三角形 D.等腰直角三角形
【答案】B
【解析】
因为 , ,
因为 ,所以 ,
因为 ,所以 ,
由此可得以 为邻边的平行四边形为矩形,所以 ,得 的形状是直角三角
形.故选B。
3.(2020·全国高一课时练习)设点M是线段BC的中点,点A在直线BC外,格致课堂
,则 ( )
A.8 B.4 C.2 D.1
【答案】C
【解析】因为 ,所以 ,
又因为 ,
所以 ,又因为 是 的中点,
所以 ,
故选C.
4.(2020·全国高一课时练习) 为平面上的定点,A,B,C是平面上不共线的三点,若
,则 是( )
A.以AB为底面的等腰三角形
B.以BC为底面的等腰三角形
C.以AB为斜边的直角三角形
D.以BC为斜边的直角三角形
【答案】B
【解析】根据题意,涉及了向量的加减法运算,以及数量积运算.
因此可知
,所以 可知为
故有 ,因此可知b=c,说明了是一个以BC为底边的等腰三角形,故选B.
⃗a,⃗b,⃗c ⃗a与⃗b
5.(多选题)设 为同一平面内具有相同起点的三个任意的非零向量。且满足 不共线,
⃗a⊥⃗c |⃗a|=|⃗c|
, ,则 的值一定等于( )格致课堂
⃗a与⃗b
A.以 为邻边的平行四边形的面积
⃗b,⃗c
B.以 为邻边的平行四边形的面积
⃗a与⃗b
C.以 为两边的三角形的面积的2倍;
⃗b,⃗c
D.以 为两边的三角形面积。
【答案】AC
【解析】设
⃗b,⃗c
的夹角为α ,
⃗a与⃗b
的夹角为 θ ,则
| ⃗b⋅⃗c|=| ⃗b||⃗c||cosα|=| ⃗b||⃗a||cos(90° ±θ)|=| ⃗b||⃗a|sinθ
,故选AC。
ΔABC
6.(多选题)点O在 所在的平面内,则以下说法正确的有( )
O⃗A+O⃗B+O⃗C=0⃗ ΔABC
A.若 ,则点O是 的重心。
⃗AC ⃗AB ⃗BC ⃗BA
O⃗A⋅( − )=O⃗B⋅( − )=0
|
⃗AC|
|
⃗AB|
|
⃗BC|
|
⃗BA|
ΔABC
B.若 ,则点O是 的垂心。
(O⃗A+O⃗B)⋅ ⃗AB=(O⃗B+O⃗C)⋅ ⃗BC=0
ΔABC
C.若 ,则点O是 的外心。
O⃗A⋅O⃗B=O⃗B⋅O⃗C=O⃗C⋅O⃗A ΔABC
D.若 ,则点O是 的内心。
【答案】AC
O⃗A=−(O⃗B+O⃗C)=−2O⃗D
【解析】选项A,设D为BC的中点,由于 ,所以O为BC边上中线
⃗AC ⃗AB
,
ΔABC |
⃗AC|
|
⃗AB|
的三等分点(靠近点D),所以点O是 的重心。选项B,向量 分别表示在边
⃗AC ⃗AB
O⃗A⋅( − )=0
⃗ AC'和 ⃗ AB' ⃗ B'C' | ⃗AC| | ⃗AB|
AC和AB上去单位向量 ,记它们的差为向量 ,则当 ,即
⃗BC ⃗BA
O⃗B⋅( − )=0
OA⊥B'C'
时,点O在
∠BAC
的平分线上,同理由
|
⃗BC|
|
⃗BA|
,知O在
∠ABC
的平格致课堂
ΔABC O⃗A+O⃗B O⃗A,O⃗B
分线上,所以点O是 的内心。选项C, 是以 为邻边的平行四边形的一条对
|
⃗AB| (O⃗A+O⃗B)⋅ ⃗AB=0
角线,而 是该平行四边形的另一条对角线, 表示这个平行四边形是菱形,
|O⃗A|=|O⃗B| |O⃗C|=|O⃗B|
ΔABC
即 , 同 理 由 , 于 是 点 O 是 的 外 心 。 选 项 D , 由
O⃗A⋅O⃗B=O⃗B⋅O⃗C O⃗A⋅O⃗B−O⃗B⋅O⃗C=0 O⃗B⋅C⃗A=0 O⃗B⊥C⃗A
得 ,所以 ,所以 ,同理可证
O⃗A⊥C⃗B,O⃗C⊥ ⃗AB
,所以
OB⊥CA
,
OA⊥BC,OC⊥AB
,即点 O 是
ΔABC
的垂心。故选
AC。
二、填空题
7.(2019·全国高一课时练习)已知 是 内一点, ,记 的面积为
, 的面积为 ,则 __________.
【答案】
【解析】
设BC中点为M,则 ,所以P到BC的距离为点A到BC距离的 ,故
8.(2019·全国高一课时练习)若点 是 所在平面内的一点,且满足 ,
则 与 的面积比为__.
【答案】
【解析】格致课堂
是 所在平面内的一点,连接 ,
延长 至 使 ,延长 至 使 ,
如图示: ,
连接 ,则四边形 是平行四边形(向量 和向量 平行且模相等)
由于 ,所以 ,所以
在平行四边形中,三角形ABD面积=三角形ABE面积=平行四边形ABED面积一半
故 与 的面积比
故答案为
9.已知 为△ 的外心,若 + − =0,则 =_____.
【答案】
【解析】
∵ + − =0,∴ ,
∴ ,
∵ 在圆 上,∴ ,∴ ∙ =0.
所以 .格致课堂
10.在四边形ABCD中, =(1,2), =(-4,2),则 与 的夹角为 ,该四
边形的面积为___________.
90°
【答案】
【解析】
试题分析:假设对角线的交点为 , 的夹角为为 ,
则四边形面积为
,
, , ,所以,两向量夹角为
90°
,四边形面积 .
三.解答题
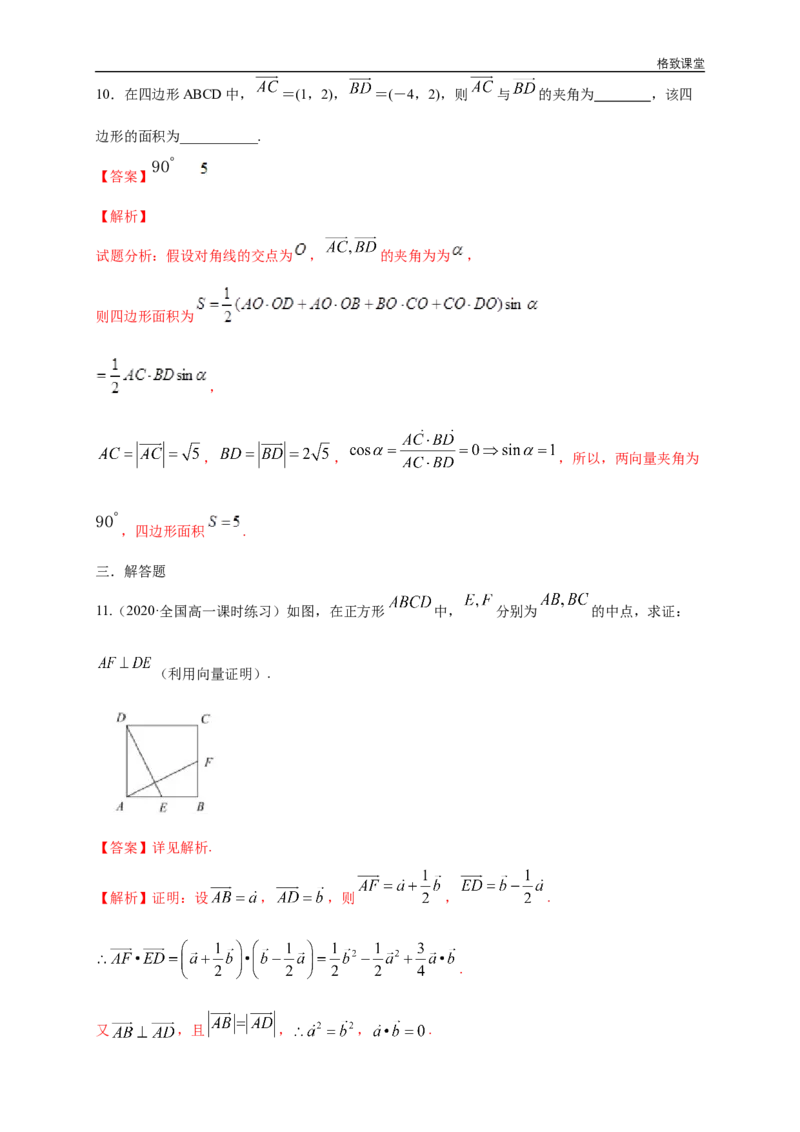
11.(2020·全国高一课时练习)如图,在正方形 中, 分别为 的中点,求证:
(利用向量证明).
【答案】详见解析.
【解析】证明:设 , ,则 , .
.
又 ,且 , , .格致课堂
, .
.
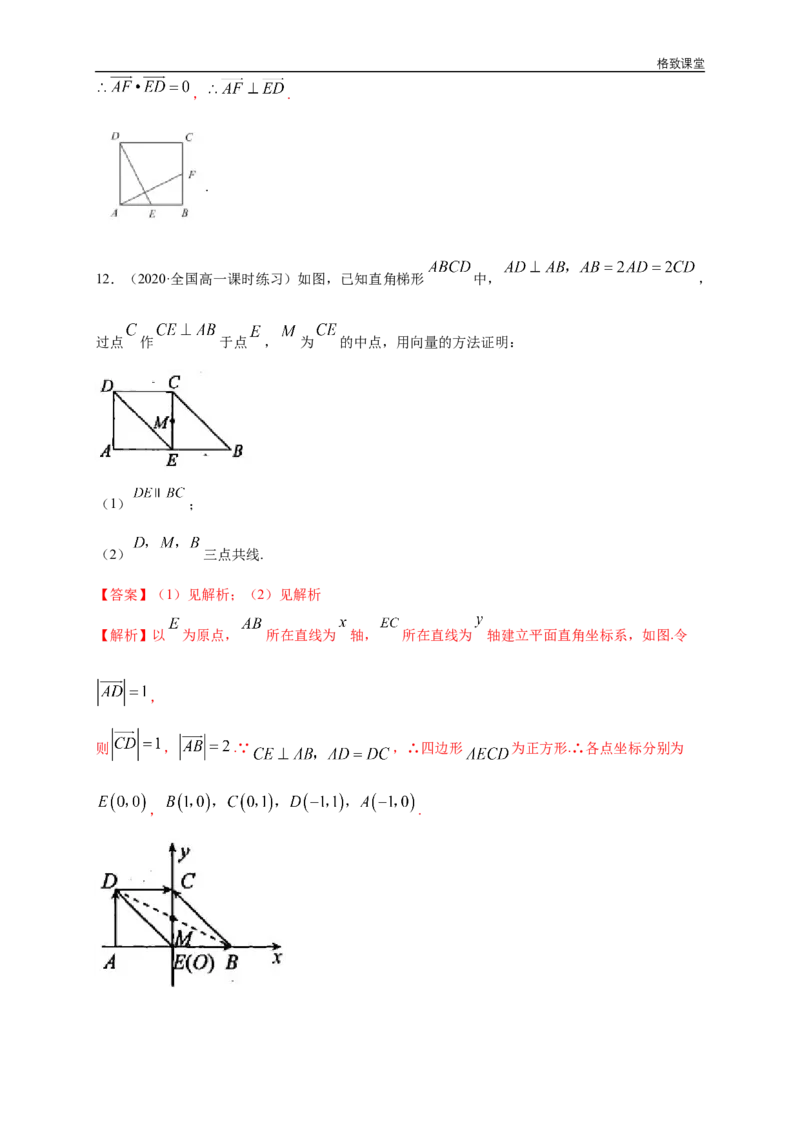
12.(2020·全国高一课时练习)如图,已知直角梯形 中, ,
过点 作 于点 , 为 的中点,用向量的方法证明:
(1) ;
(2) 三点共线.
【答案】(1)见解析;(2)见解析
【解析】以 为原点, 所在直线为 轴, 所在直线为 轴建立平面直角坐标系,如图.令
,
则 , .∵ ,∴四边形 为正方形.∴各点坐标分别为
, .格致课堂
(1)∵ , ,
∴ ,∴ ,即 .
(2)∵ 为 的中点,∴ ,∴ ,
.∵ ,
∴ .又∵ 与 有公共点,∴ 三点共线.