文档内容
格致课堂
6.4.3 余弦定理、正弦定理
第 3 课时 余弦定理、正弦定理应用举例
(用时45分钟)
【选题明细表】
知识点、方法 题号
余弦定理、正弦定理应用举例 1,2,3,4,5,6,7,8,9,10,11,12
基础巩固
1.若点 在点 的北偏东 方向上,则点 在点 的( )
A.东偏北 方向上 B.北偏东 方向上
C.南偏西 方向上 D.西偏南 方向上
【答案】C
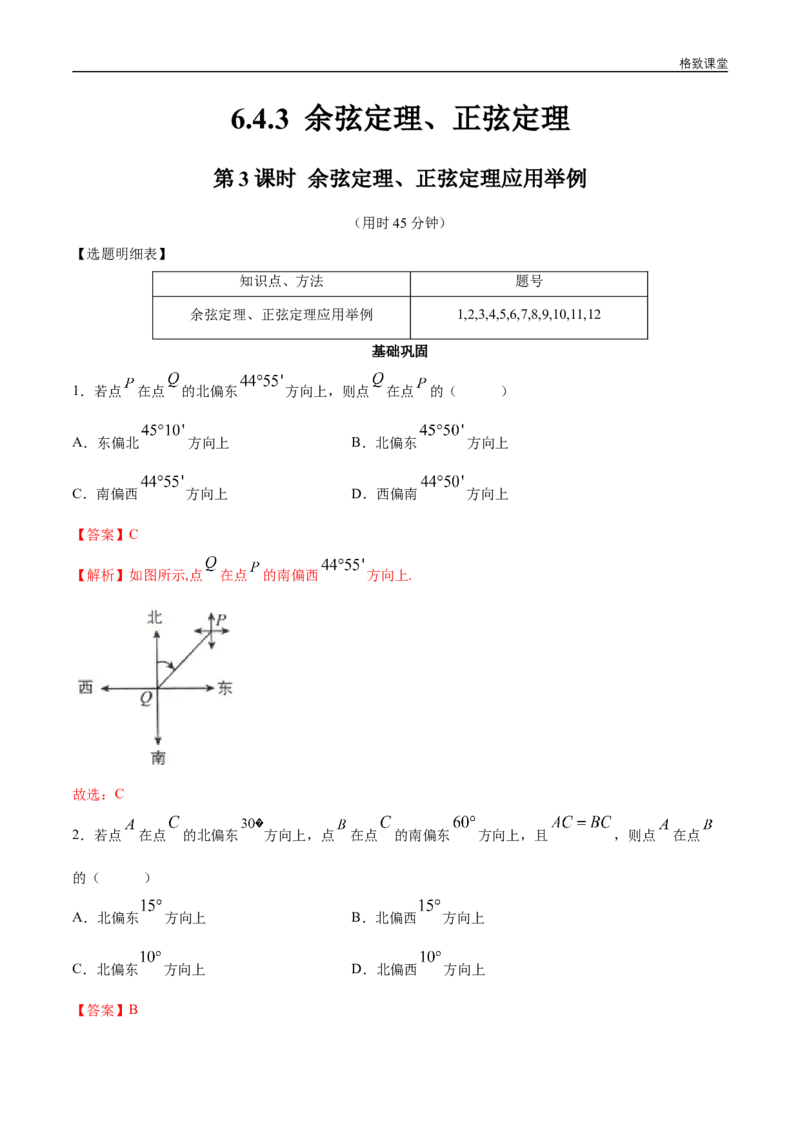
【解析】如图所示,点 在点 的南偏西 方向上.
故选:C
2.若点 在点 的北偏东 方向上,点 在点 的南偏东 方向上,且 ,则点 在点
的( )
A.北偏东 方向上 B.北偏西 方向上
C.北偏东 方向上 D.北偏西 方向上
【答案】B格致课堂
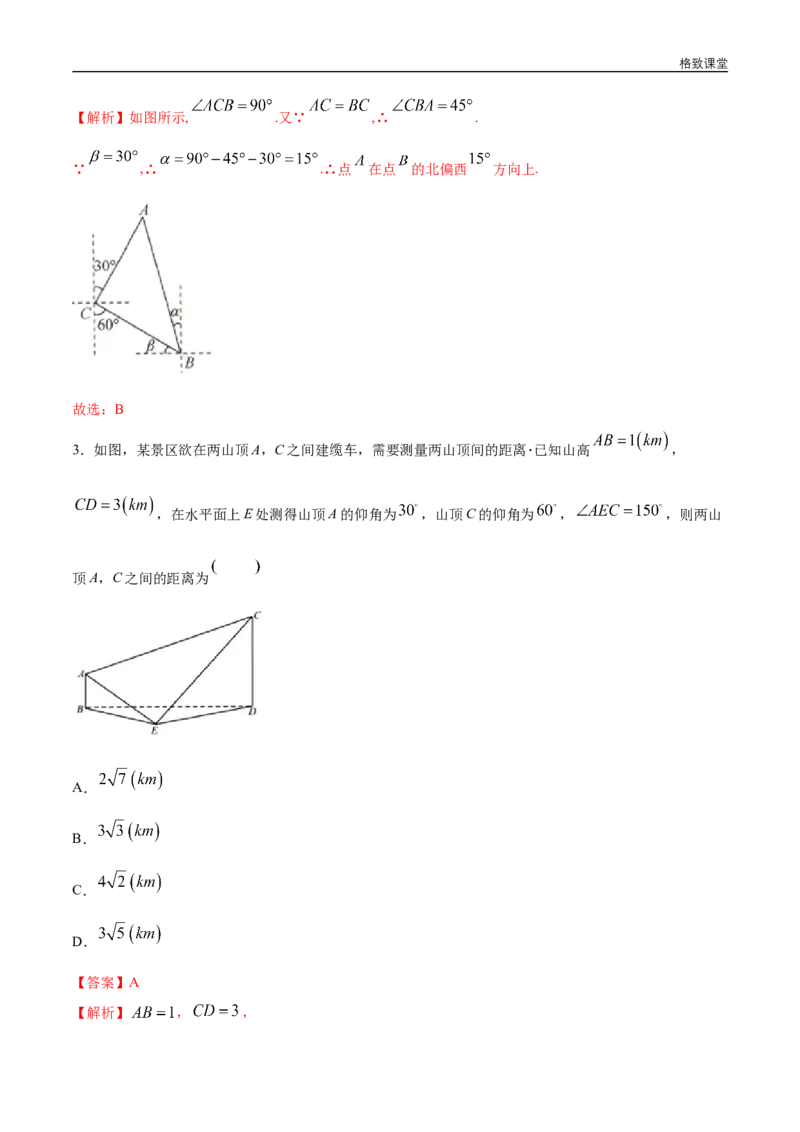
【解析】如图所示, .又∵ ,∴ .
∵ ,∴ .∴点 在点 的北偏西 方向上.
故选:B
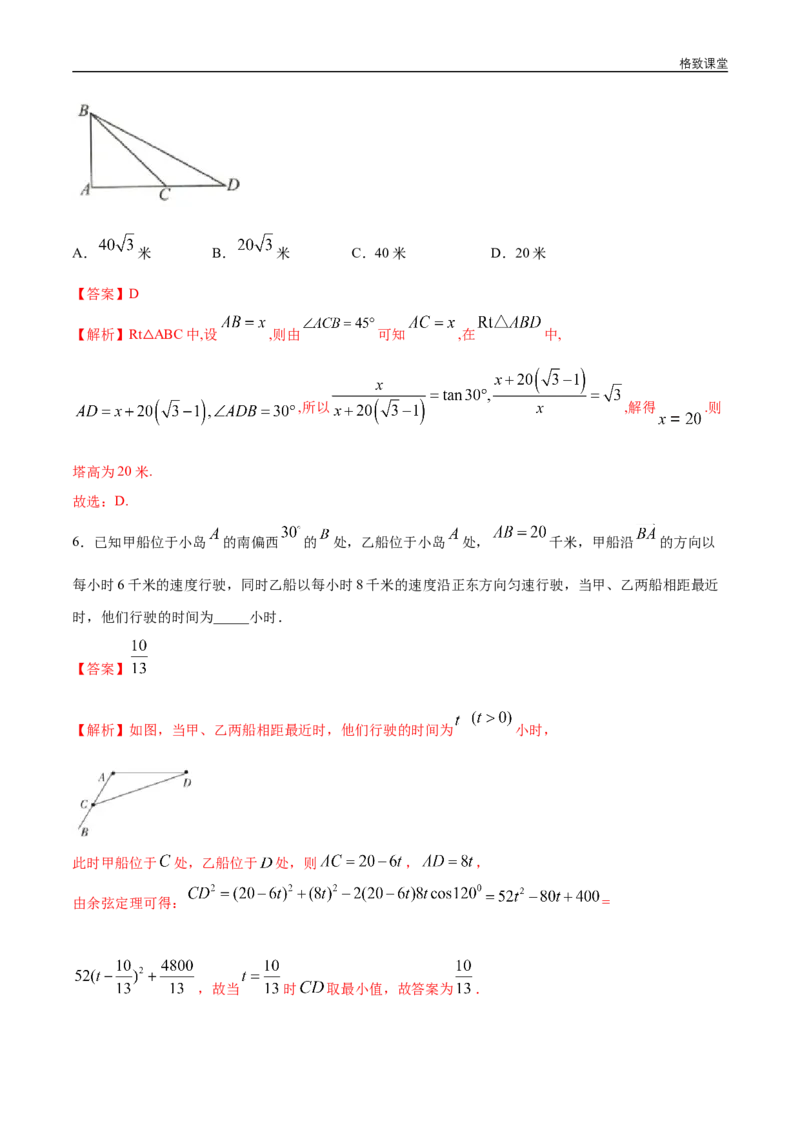
3.如图,某景区欲在两山顶A,C之间建缆车,需要测量两山顶间的距离 已知山高 ,
,在水平面上E处测得山顶A的仰角为 ,山顶C的仰角为 , ,则两山
顶A,C之间的距离为
A.
B.
C.
D.
【答案】A
【解析】 , ,格致课堂
, , ,
, ;
ACE中,由余弦定理得
△
,
;
即两山顶A,C之间的距离为 .
故选A.
4.一海轮从A处出发,以每小时40海里的速度沿南偏东40°的方向直线航行,30分钟后到达B处.在C
处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么
B,C两点间的距离是( )
A.10 海里 B.10 海里 C.20 海里 D.20 海里
【答案】B
【解析】根据已知条件可知△ABC中,AB=20,∠BAC=30°,∠ABC=105°,所以∠C=45°,
由正弦定理,有 ,所以 10 .
故选B.
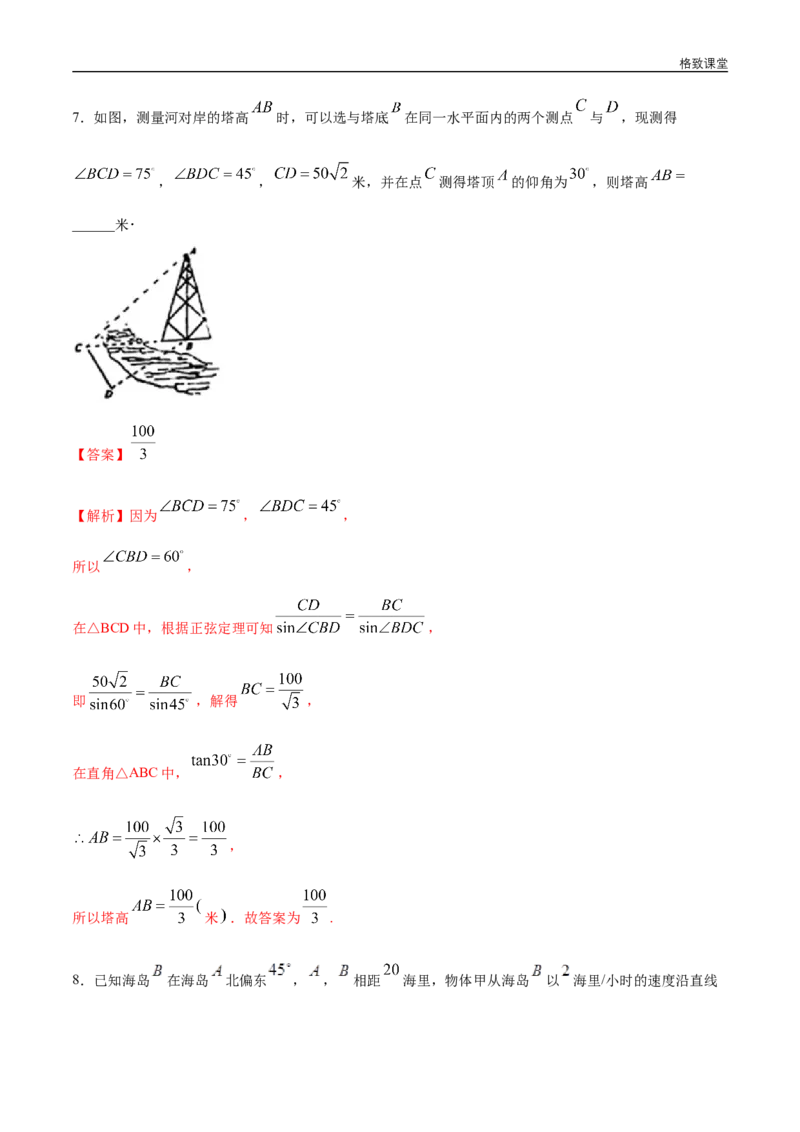
5.如图,为测塔 的高度,某人在与塔底 同一水平线上的 点测得 ,再沿 方向前行
米到达 点,测得 ,则塔高为( )格致课堂
A. 米 B. 米 C.40米 D.20米
【答案】D
【解析】Rt ABC中,设 ,则由 可知 ,在 中,
△
,所以 ,解得 .则
塔高为20米.
故选:D.
6.已知甲船位于小岛 的南偏西 的 处,乙船位于小岛 处, 千米,甲船沿 的方向以
每小时6千米的速度行驶,同时乙船以每小时8千米的速度沿正东方向匀速行驶,当甲、乙两船相距最近
时,他们行驶的时间为_____小时.
【答案】
【解析】如图,当甲、乙两船相距最近时,他们行驶的时间为 小时,
此时甲船位于 处,乙船位于 处,则 , ,
由余弦定理可得: =
,故当 时 取最小值,故答案为 .格致课堂
7.如图,测量河对岸的塔高 时,可以选与塔底 在同一水平面内的两个测点 与 ,现测得
, , 米,并在点 测得塔顶 的仰角为 ,则塔高
______米
【答案】
【解析】因为 , ,
所以 ,
在△BCD中,根据正弦定理可知 ,
即 ,解得 ,
在直角△ABC中, ,
,
所以塔高 米 .故答案为 .
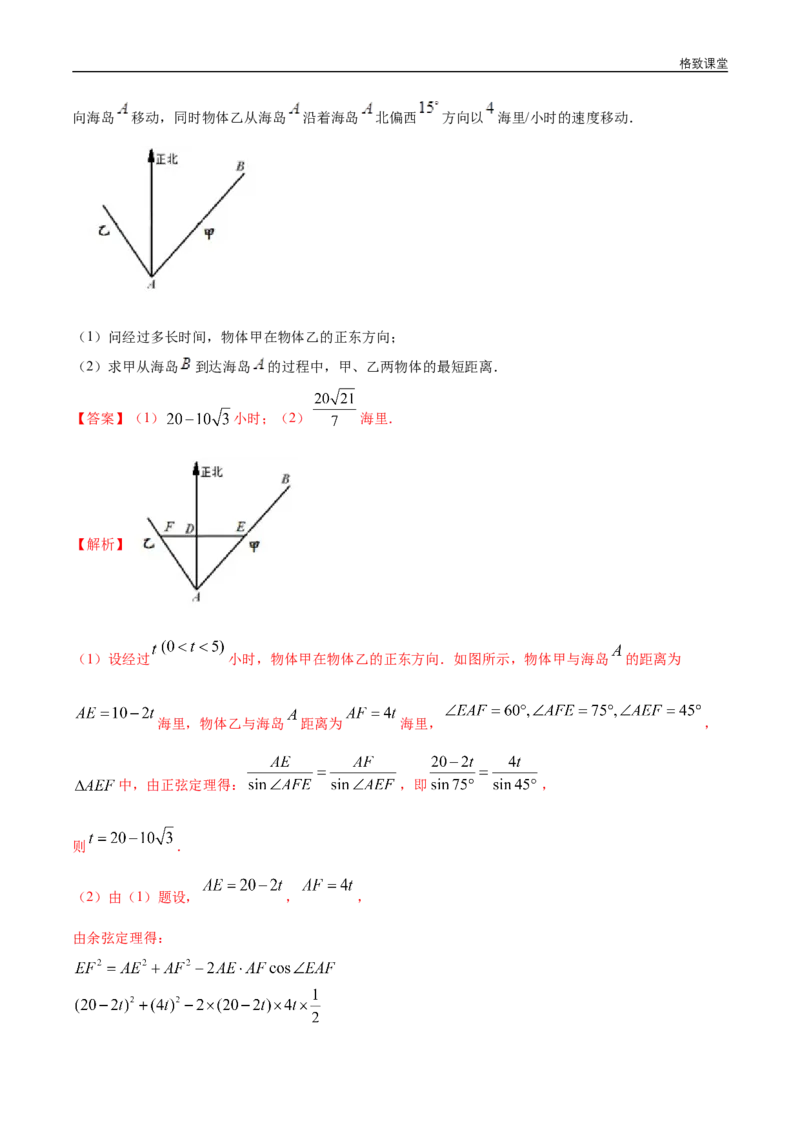
8.已知海岛 在海岛 北偏东 , , 相距 海里,物体甲从海岛 以 海里/小时的速度沿直线格致课堂
向海岛 移动,同时物体乙从海岛 沿着海岛 北偏西 方向以 海里/小时的速度移动.
(1)问经过多长时间,物体甲在物体乙的正东方向;
(2)求甲从海岛 到达海岛 的过程中,甲、乙两物体的最短距离.
【答案】(1) 小时;(2) 海里.
【解析】
(1)设经过 小时,物体甲在物体乙的正东方向.如图所示,物体甲与海岛 的距离为
海里,物体乙与海岛 距离为 海里, ,
中,由正弦定理得: ,即 ,
则 .
(2)由(1)题设, , ,
由余弦定理得:格致课堂
∵ ,
∴当 时, 海里.
能力提升
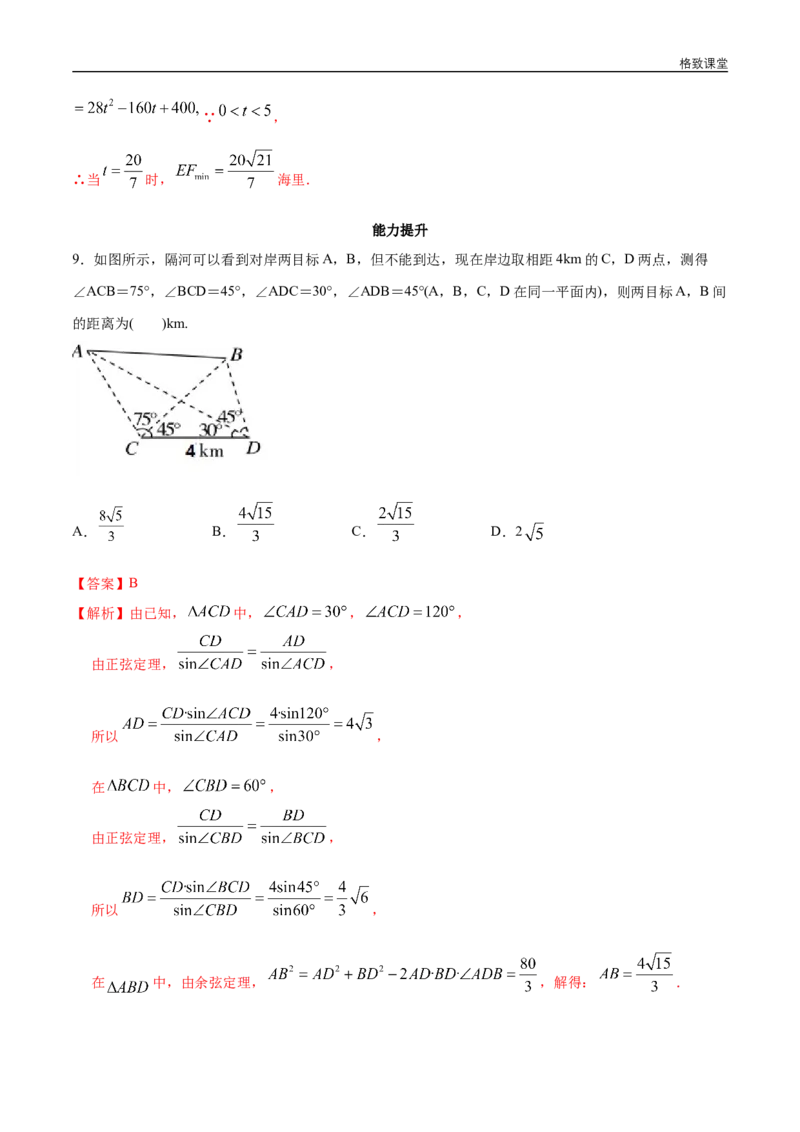
9.如图所示,隔河可以看到对岸两目标A,B,但不能到达,现在岸边取相距4km的C,D两点,测得
∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),则两目标A,B间
的距离为( )km.
A. B. C. D.2
【答案】B
【解析】由已知, 中, , ,
由正弦定理, ,
所以 ,
在 中, ,
由正弦定理, ,
所以 ,
在 中,由余弦定理, ,解得: .格致课堂
所以 与 的距离 .
故选B
10.如图,为了测量河对岸 、 两点之间的距离,观察者找到一个点 ,从点 可以观察到点 、 ;
找到一个点 ,从点可以观察到点 、 ;找到一个点 ,从点可以观察到点 、 ;并测量得到一些
数据: , , , , , ,
,则 、 两点之间的距离为__________.(其中 取近似值 )
【答案】
【解析】由题意知,在△ACD中, .
由正弦定理得 .
在△BCE中, ,由正弦定理得
在△ABC中,由余弦定理得 ,∴
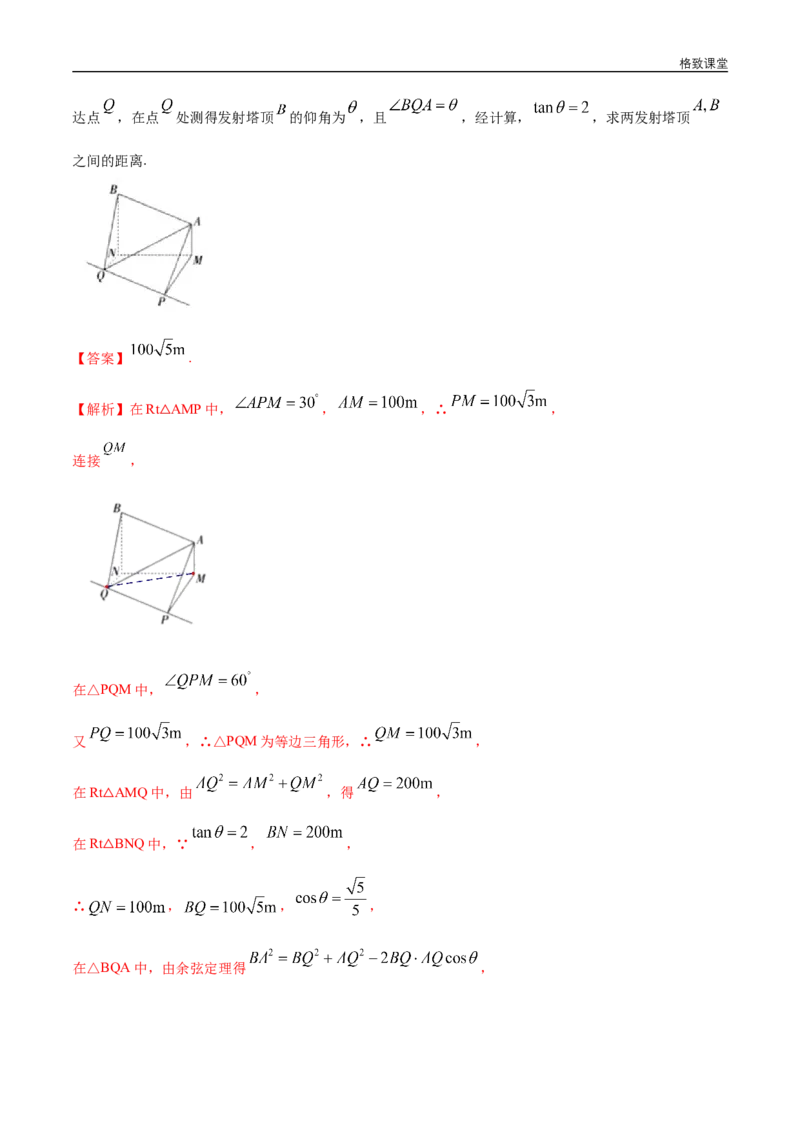
11.如图,已知在东西走向上有 两座发射塔,且 , ,一辆测量车在塔
底 的正南方向的点 处测得发射塔顶 的仰角为30°,该测量车向北偏西60°方向行驶了 后到格致课堂
达点 ,在点 处测得发射塔顶 的仰角为 ,且 ,经计算, ,求两发射塔顶
之间的距离.
【答案】 .
【解析】在Rt AMP中, , ,∴ ,
△
连接 ,
在△PQM中, ,
又 ,∴△PQM为等边三角形,∴ ,
在Rt AMQ中,由 ,得 ,
△
在Rt BNQ中,∵ , ,
△
∴ , , ,
在△BQA中,由余弦定理得 ,格致课堂
∴ ,
∴两发射塔顶 之间的距离是 .
素养达成
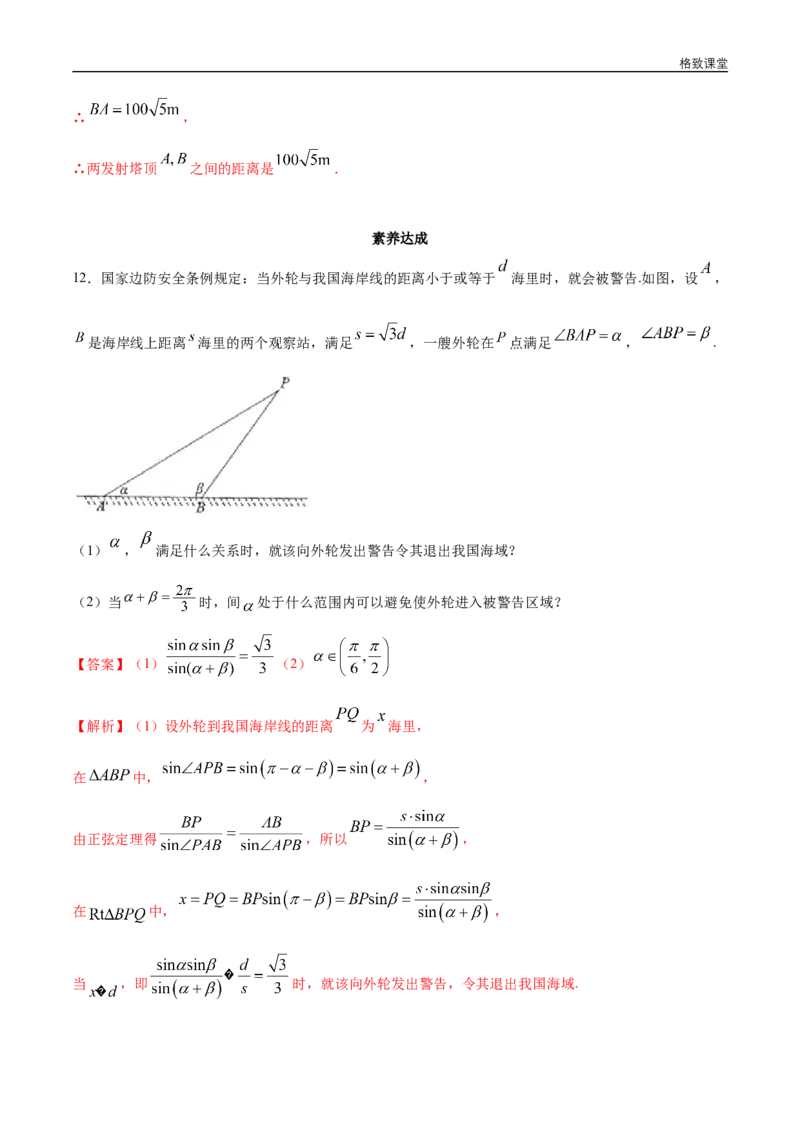
12.国家边防安全条例规定:当外轮与我国海岸线的距离小于或等于 海里时,就会被警告.如图,设 ,
是海岸线上距离 海里的两个观察站,满足 ,一艘外轮在 点满足 , .
(1) , 满足什么关系时,就该向外轮发出警告令其退出我国海域?
(2)当 时,间 处于什么范围内可以避免使外轮进入被警告区域?
【答案】(1) (2)
【解析】(1)设外轮到我国海岸线的距离 为 海里,
在 中, ,
由正弦定理得 ,所以 ,
在 中, ,
当 ,即 时,就该向外轮发出警告,令其退出我国海域.格致课堂
(2)当 时,
,
要使不被警告,则 ,即 ,
解得 ,所以 ,
即 ,又因为 ,所以 .
当 时可以避免使外轮进入被警告区域.