文档内容
格致课堂
6.4.2 向量在物理中的应用举例
(用时45分钟)
【选题明细表】
知识点、方法 题号
向量在物理中的应用 1,2,3,4,5,6,7,8,9,10,11,12
基础巩固
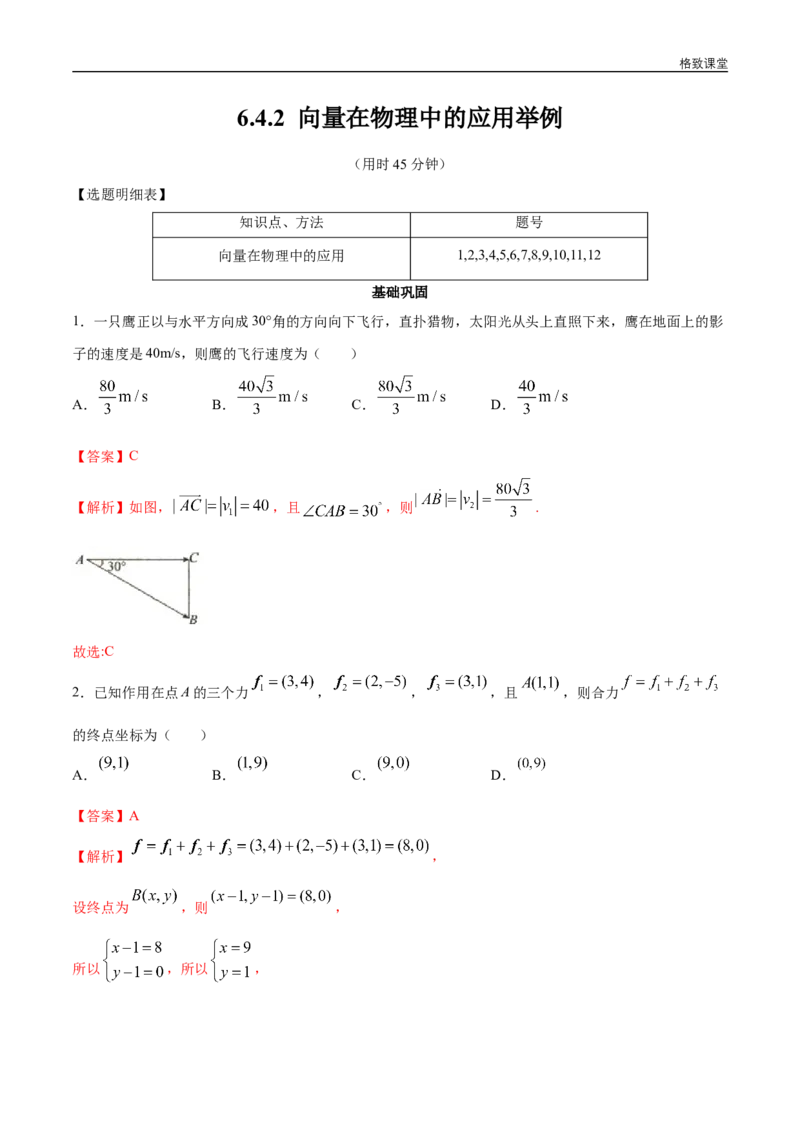
1.一只鹰正以与水平方向成30°角的方向向下飞行,直扑猎物,太阳光从头上直照下来,鹰在地面上的影
子的速度是40m/s,则鹰的飞行速度为( )
A. B. C. D.
【答案】C
【解析】如图, ,且 ,则 .
故选:C
2.已知作用在点A的三个力 , , ,且 ,则合力
的终点坐标为( )
A. B. C. D.
【答案】A
【解析】 ,
设终点为 ,则 ,
所以 ,所以 ,格致课堂
所以终点坐标为 .
3.两个大小相等的共点力 ,当它们夹角为 时,合力大小为 ,则当它们的夹角为 时,
合力大小为( )
A. B. C. D.
【答案】B
【解析】设合力为 ,
由平行四边形法则可知, ,
当 和 的夹角为 时,由平行四边形法则, ,
故选:B.
4.人骑自行车的速度是 ,风速为 ,则逆风行驶的速度为( )
A. B. C. D.
【答案】B
【解析】由题意,根据向量的加法法则,可得逆风行驶的速度为 ,注意速度是有方向和大小的,是
一个向量.
故选:B.
5.点P在平面上作匀速直线运动,速度v=(4,-3),设开始时点P的坐标为(-10,10),则5秒后点P的坐
标为(速度单位:m/s,长度单位:m) ( )
A.(-2,4) B.(-30,25)格致课堂
C.(10,-5) D.(5,-10)
【答案】C
【解析】5秒后点P的坐标为:(-10,10)+5(4,-3)=(10,-5).
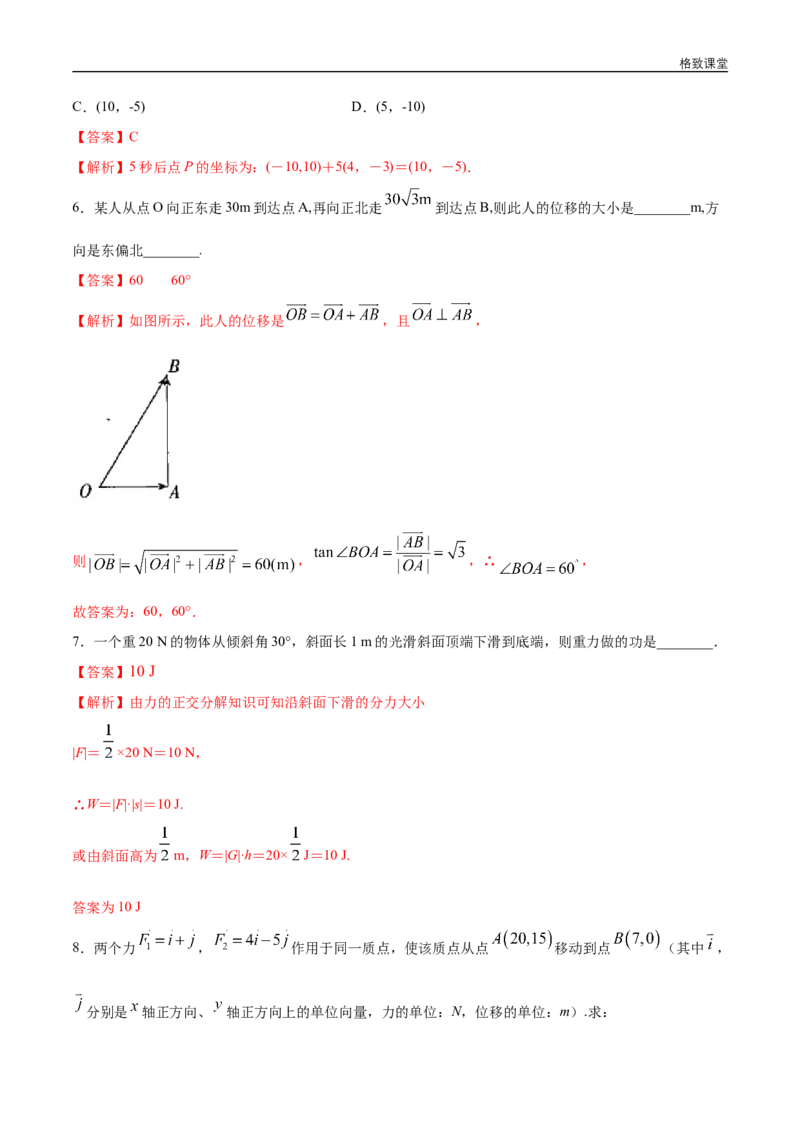
6.某人从点O向正东走30m到达点A,再向正北走 到达点B,则此人的位移的大小是________m,方
向是东偏北________.
【答案】60 60°
【解析】如图所示,此人的位移是 ,且 ,
则 , ,∴ ,
故答案为:60,60°.
7.一个重20 N的物体从倾斜角30°,斜面长1 m的光滑斜面顶端下滑到底端,则重力做的功是________.
【答案】10 J
【解析】由力的正交分解知识可知沿斜面下滑的分力大小
|F|= ×20 N=10 N,
∴W=|F|·|s|=10 J.
或由斜面高为 m,W=|G|·h=20× J=10 J.
答案为10 J
8.两个力 , 作用于同一质点,使该质点从点 移动到点 (其中 ,
分别是 轴正方向、 轴正方向上的单位向量,力的单位:N,位移的单位:m).求:格致课堂
(1) , 分别对该质点做的功;
(2) , 的合力 对该质点做的功.
【答案】(1) 做的功 , 做的功 .
(2)
【解析】(1) , , .
做的功 ,
做的功 .
(2) ,
所以 做的功 .
能力提升
9.一条河的宽度为 ,一只船从 处出发到河的正对岸 处,船速为 ,水速为 ,则船行到 处时,
行驶速度的大小为( )
A. B. C. D.
【答案】D
【解析】如图所示,由平行四边形法则和解直角三角形的知识,
可得船行驶的速度大小为 .
故选:D.格致课堂
10.如图,两根固定的光滑硬杆OA,OB成 角,在杆上分别套一小环P,Q(小环重力不计),并用轻
线相连.现用恒力F沿 方向拉小环Q,则当两环稳定时,轻线上的拉力的大小为__________.
【答案】 .
【解析】以小环 为研究对象,由于受力平衡,故轻线与杆 垂直,
即轻线与杆 的夹角为 .
设小环 受轻线的拉力为 ,对其受力分析,
可得在水平方向上有 ,
故 .
故答案为: .
11.如图所示,一条河的两岸平行,河的宽度 ,一艘船从 点出发航行到河对岸,船航行速度
的大小为 ,水流速度的大小为 ,设 和 的夹角 .
(1)当 多大时,船能垂直到达对岸?
(2)当船垂直到达对岸时,航行所需时间是否最短?为什么?格致课堂
【答案】(1) ;(2)当 时,船的航行时间最短,而当船垂直到达对岸,所需时间并
不是最短.
【解析】(1)船垂直到达对岸,即 与 垂直,即 .
所以 ,即 .
所以 ,解得 .
(2)设船航行到对岸所需的时间为 ,
则 .
故当 时,船的航行时间最短,而当船垂直到达对岸,所需时间并不是最短.
素养达成
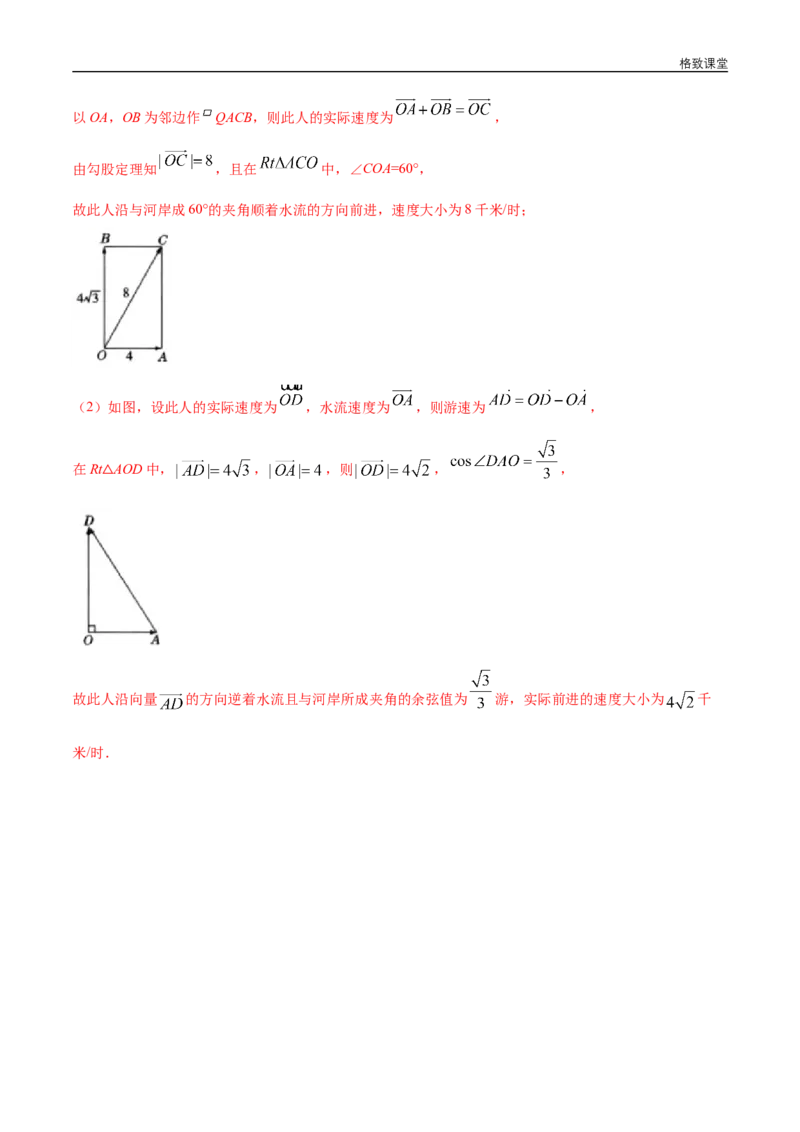
12.某人在静水中游泳,速度为 千米/时,现在他在水流速度为4千米/时的河中游泳.
(1)若他沿垂直于岸边的方向游向河对岸,则他实际沿什么方向前进?实际前进的速度大小为多少?
(2)他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度大小为多少?
【答案】(1)沿与河岸成60°的夹角顺着水流的方向前进,速度大小为8千米/时 (2)沿向量 的方
向逆着水流且与河岸所成夹角的余弦值为 游,实际前进的速度大小为 千米/时
【解析】(1)如图,设此人游泳的速度为 ,水流的速度为 ,格致课堂
以OA,OB为邻边作 QACB,则此人的实际速度为 ,
由勾股定理知 ,且在 中,∠COA=60°,
故此人沿与河岸成60°的夹角顺着水流的方向前进,速度大小为8千米/时;
(2)如图,设此人的实际速度为 ,水流速度为 ,则游速为 ,
在Rt AOD中, , ,则 , ,
△
故此人沿向量 的方向逆着水流且与河岸所成夹角的余弦值为 游,实际前进的速度大小为 千
米/时.