文档内容
格致课堂
6.4.3 余弦定理、正弦定理
第 2 课时 正弦定理
(用时45分钟)
【选题明细表】
知识点、方法 题号
解三角形 1,2,6,8
性质应用 3,4,5,9
面积公式应用 7,10,11,12
基础巩固
1.在 中, ,则∠ 等于( )
A.30°或150° B.60° C.60°或120° D.30°
【答案】C
【解析】根据正弦定理 ,
可得 ,解得 ,故可得 为60°或120°;
又 ,则 ,显然两个结果都满足题意.
故选:C.
2.在 中,内角 所对的边分别为 ,已知 , , ,则 ( )
A. B. C. D.
【答案】A
【解析】 在 中, , ,
,格致课堂
再由正弦定理 ,即
解得 .故选A.
3.在△ABC中,角A,B,C的对边分别是a,b,c,若A∶B∶C=1∶2∶3,则a∶b∶c等于( )
A.1∶2∶3 B.2∶3∶4 C.3∶4∶5 D.1∶ ∶2
【答案】D
【解析】由题可得:A=30°,B=60°,C=90°,由正弦定理: ,故选
D.
4.设在 中,角 所对的边分别为 , 若 , 则 的形状为
( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
【答案】B
【解析】因为 ,
所以由正弦定理可得 ,
,
所以 ,所以是直角三角形.
5.在 中,角 , , 的对边分别是 , , ,且 ,则角 的大小为
( )
A. B. C. D.
【答案】B
【解析】由正弦定理得 ,即 ,即格致课堂
,也即 ,故 ,所以选B.
6.在 中,若 ,则 边上的高是________.
【答案】 或
【解析】由 ,得 ,
或 .
当 时, , 边上的高为 ;
当 时, , 边上的高为 .
故答案为: 或
7.设 的内角A,B,C的对边分别为 , , 且 , , ,则
__________.
【答案】1
【解析】∵ ,
∴由正弦定理可得 .
又∵ ,
∴由余弦定理 ,可得 ,
解得 或 ,
因 ,故 .
故答案为: .
8.已知在 中,内角 所对的边分别为 . ,求角 和边 .格致课堂
【答案】当 时, , ;当 时, ,
【解析】由正弦定理 ,得 ,因为 ,所以 或 ,
当 时, ,此时 ;
当 时, ,此时 .
能力提升
9.在 中,内角 , , 所对的边分别为 , , ,若 , , ,则
的外接圆的面积为( )
A. B. C. D.
【答案】B
【解析】在 中, , ,
所以 .
设 的外接圆的半径为R,
则由正弦定理,可得 ,
解得
故 的外接圆的面积 ,
故选:B.
10.在 中,a,b,c分别是 , , 的对边 已知 , , 的面积为格致课堂
,则 ______.
【答案】
【解析】 三角形的面积 ,
,
即 ,
则 ,
即 ,
故答案为: .
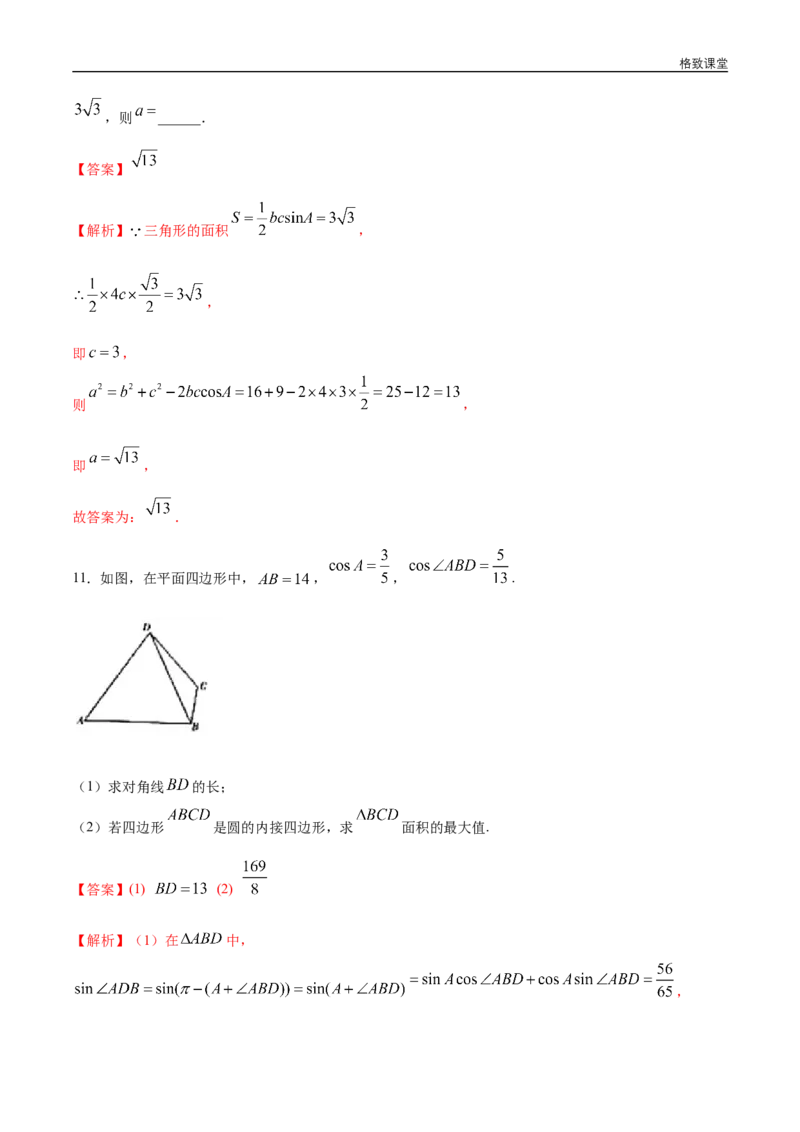
11.如图,在平面四边形中, , , .
(1)求对角线 的长;
(2)若四边形 是圆的内接四边形,求 面积的最大值.
【答案】(1) (2)
【解析】(1)在 中,
,格致课堂
由正弦定理得 ,
即 .
(2)由已知得, ,所以 ,
在 中,由余弦定理可得 ,
则 ,
即 ,
所以 ,
当且仅当 时取等号.
素养达成
12.设 的内角A,B,C所对的边分别为 ,且 .
(1)求角A的大小;
(2)若 ,求 的周长的取值范围
【答案】(1) ;(2) .
【解析】(1)由 及正弦定理,得 .
又∵ ,∴ ,格致课堂
∴ .
∵ ,∴ ,∴ .又∵ ,∴ .
(2)由正弦定理,得 ,
∴ .
∵ ,∴ ,
∴ ,
∴ 的周长的取值范围为