文档内容
格致课堂
6.4.3 余弦定理、正弦定理
第 1 课时 余弦定理
(用时45分钟)
【选题明细表】
知识点、方法 题号
解三角形 1,3,6,7,8,10
边角互化 2,4,5,9
综合应用 11,12
基础巩固
1.△ABC中,内角 的对边分别为 .若 ,则 ( )
A. B. C.2 D.3
【答案】B
【解析】由余弦定理可得 ,所以 ,
故选:B.
2.在△ABC中,角A、B、C的对边分别为a、b、c,若 ,则角B的值为(
)
A. B. C. 或 D. 或
【答案】D
【解析】∵ ,∴ .
∴cosB ,格致课堂
∴sinB ,B∈(0,π).
∴B 或 .
故选D.
3.边长分别为1, , 的三角形的最大角与最小角的和是( )
A. B. C. D.
【答案】C
【解析】由题意可得,边长为 的边对的角不是最大角、也不是最小角,
设此角为 ,则由余弦定理可得 ,∴ ,
故三角形的最大角与最小角的和是 ,故选C.
4. 的内角 所对的边分别是 ,已知 ,则 ( )
A. B. C. D.
【答案】C
【解析】根据题意,若 ,
则有: ,
整理得: ,
可得: ,
又在△ABC中, ,
.格致课堂
故选C.
5. 的三内角 所对边的长分别为 设向量 , ,若 ,则角 的大
小为( )
A. B. C. D.
【答案】B
【解析】因为两向量平行,所以等价于 ,整理为 ,所以
,所以角
6.已知 中, , , ,则 = .
【答案】1或2
【解析】由余弦定理得 ,即 ,解得
或 .
7.在不等边△ABC中, 为最大边,若 ,则 的取值范围为________.
【答案】
【解析】∵ ,∴ ,则 .
∴ .又∵ 为最大边,∴ .
故 的取值范围是 .
故答案为:
8.在 ABC中,已知 , , ,解三角形.格致课堂
【答案】 ,
【解析】∵
= cos
= =
∴
∵cos
∴
能力提升
9.△ABC中, 分别表示角 所对的边,若 ,则 的值等于( )
A. B. C. D.
【答案】A
【解析】由 得 ,
所以 ,
故选:A
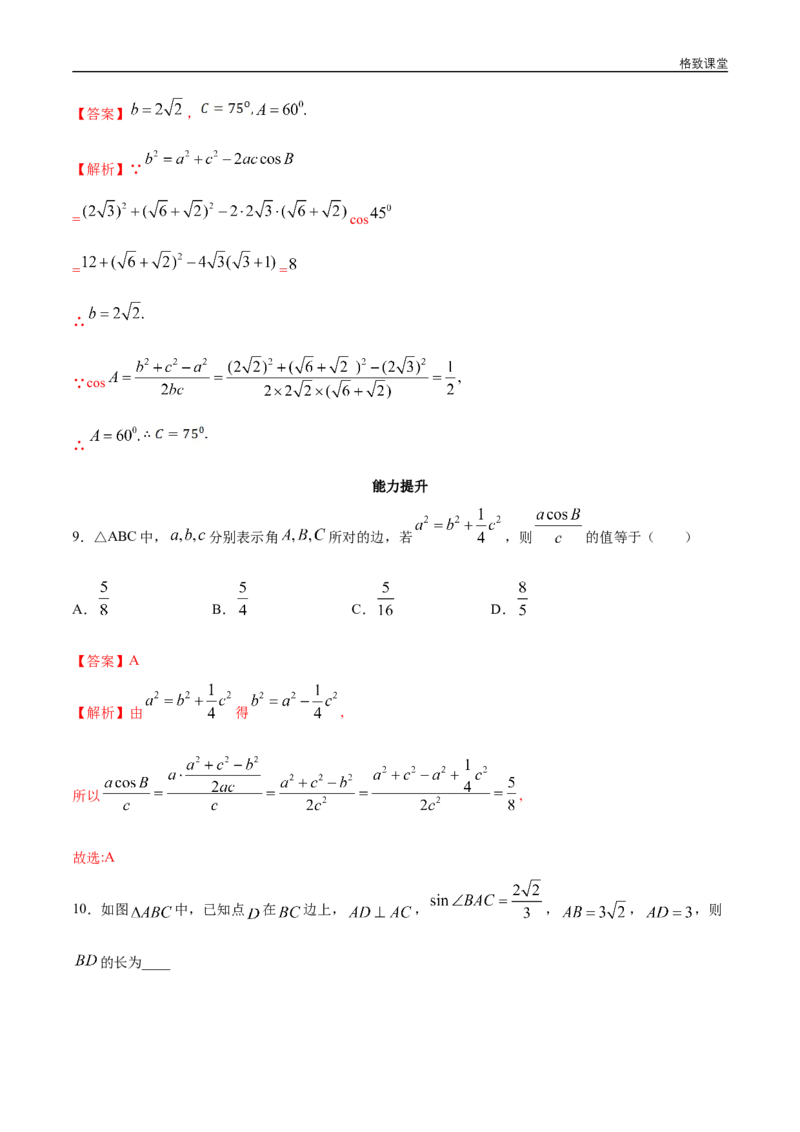
10.如图 中,已知点 在 边上, , , , ,则
的长为____格致课堂
【答案】
【解析】 , ,
,
又 , ,
,
,
故答案为: .
11.在△ABC中,内角 的对边分别为 ,且 .
(1)求 的大小;
(2)求 的值.
【答案】(1) (2)
【解析】(1)在△ABC中,∵ ,∴ ,
∴ ,∴ ,解得 或格致课堂
(舍去).又∵ ,∴ .
(2)∵ .∴在 中,由余弦定理,得 ,∴
.
素养达成
12.在 中,角 的对边分别为 ,且 .
(1)求 的值;
(2)求 的值.
【答案】(1) (2)
【解析】(1)由 ,得 ,
根据余弦定理得 ;
(2)由 ,得 ,
∴ , ,
∴ .