文档内容
格致课堂
6.4.3 余弦定理、正弦定理
第3课时 余弦定理、正弦定理的应用举例
一、选择题
1.某人向正东走了x km后向右转了150°,然后沿新方向走3 km,结果离出发点恰好 km,那么x的
值是( )
A. B. C.3 D. 或
【答案】D
【解析】
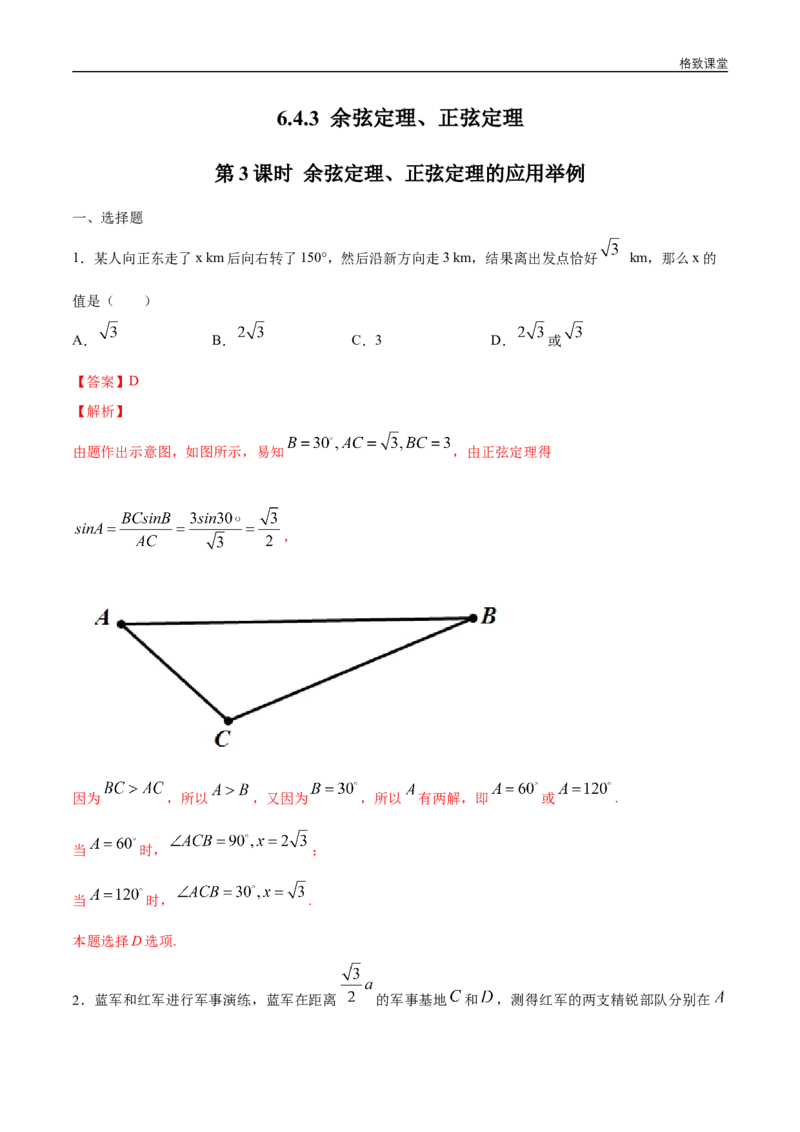
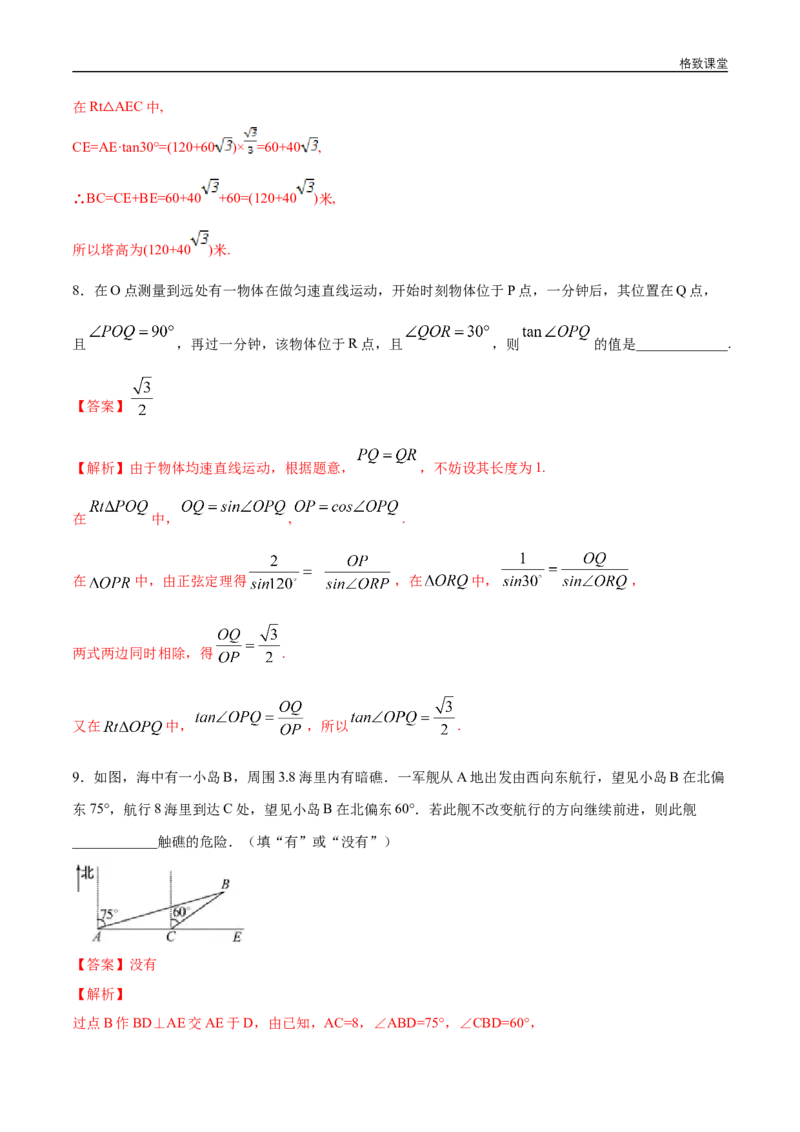
由题作出示意图,如图所示,易知 ,由正弦定理得
,
因为 ,所以 ,又因为 ,所以 有两解,即 或 .
当 时, ;
当 时, .
本题选择D选项.
2.蓝军和红军进行军事演练,蓝军在距离 的军事基地 和 ,测得红军的两支精锐部队分别在格致课堂
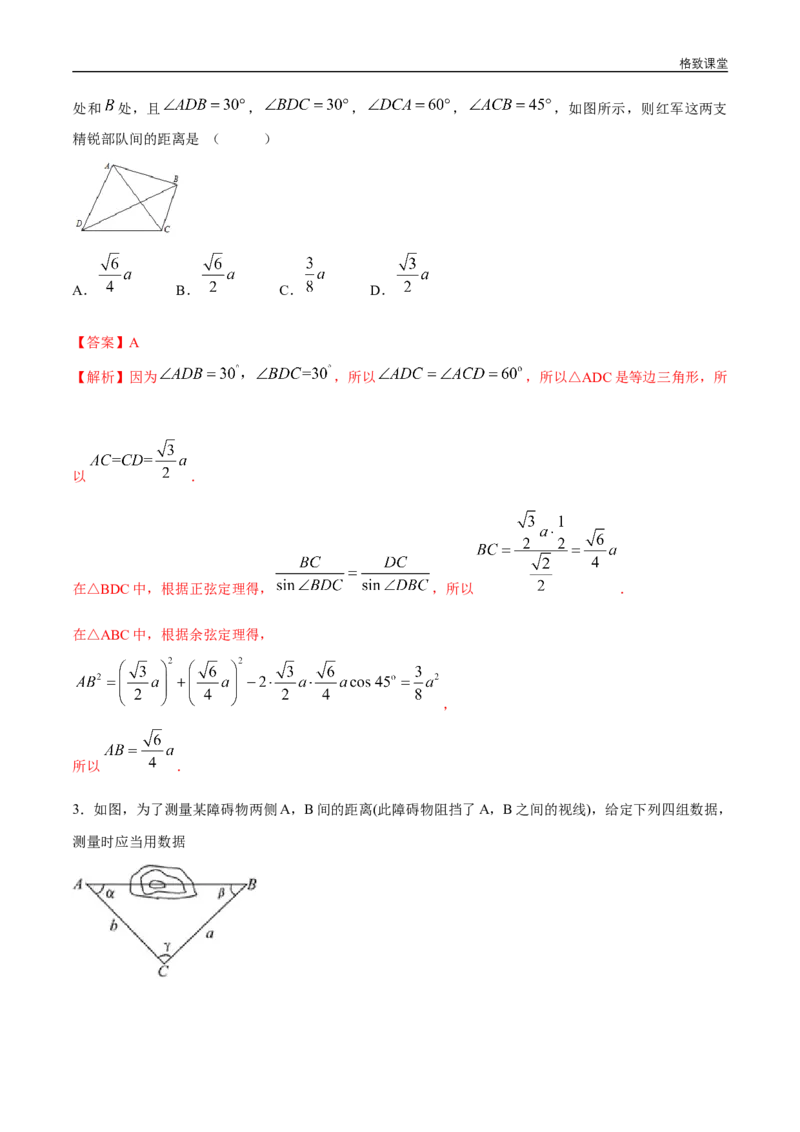
处和 处,且 , , , ,如图所示,则红军这两支
精锐部队间的距离是 ( )
A. B. C. D.
【答案】A
【解析】因为 ,所以 ,所以△ADC是等边三角形,所
以 .
在△BDC中,根据正弦定理得, ,所以 .
在△ABC中,根据余弦定理得,
,
所以 .
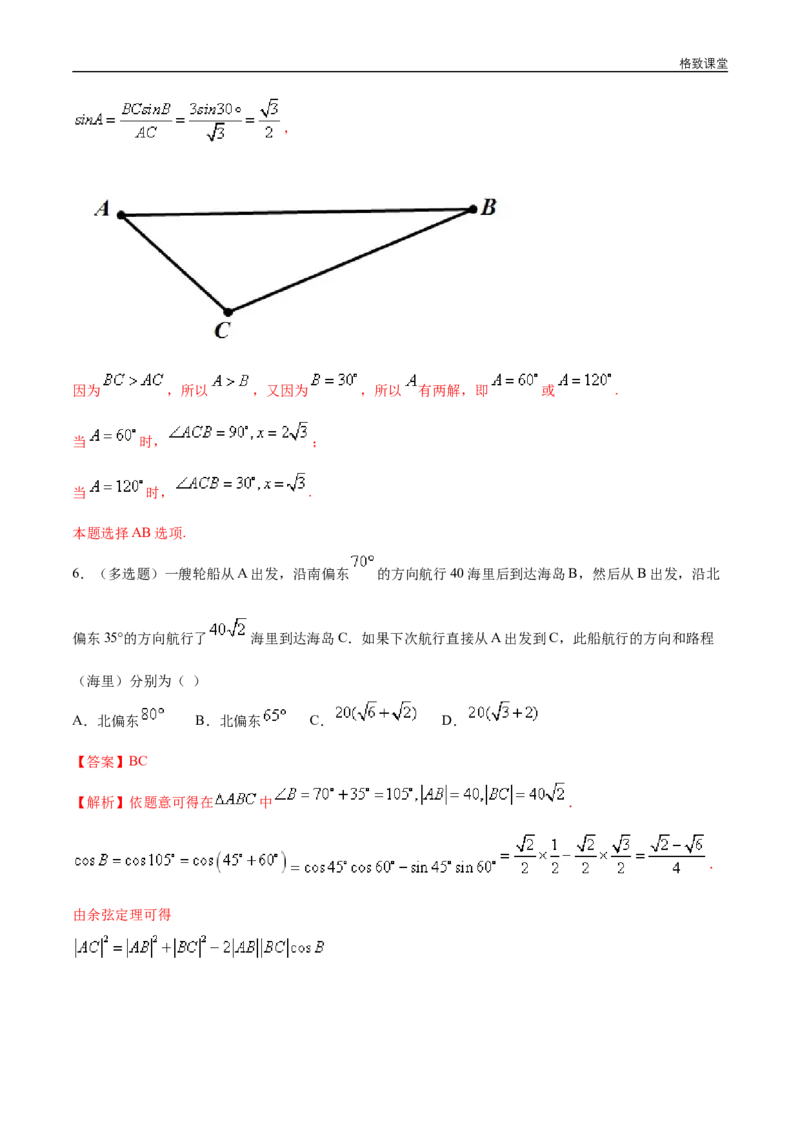
3.如图,为了测量某障碍物两侧A,B间的距离(此障碍物阻挡了A,B之间的视线),给定下列四组数据,
测量时应当用数据格致课堂
A. B. C. D.
【答案】C
【解析】
由余弦定理 知,需要测量数据 .故选C.
4.如图所示,长为 的木棒 斜靠在石堤旁,木棒的一端 在离堤足 处 的地面上,另一端
在离堤足 处 的石堤上,石堤的倾斜角为 ,则坡度值 等于 ( )
A. B. C. D.
【答案】C
【解析】由题意可得,在△ABC中,AB=4m,AC=2m,BC=3m,且 +∠ACB=π.
由余弦定理可得, ,即
,解得 ,所以 ,所以 .
5.(多选题)某人向正东走了x km后向右转了150°,然后沿新方向走3 km,结果离出发点恰好 km,
那么x的值是( )
A. B. C.3 D.6
【答案】AB
【解析】由题作出示意图,如图所示,易知 ,由正弦定理得格致课堂
,
因为 ,所以 ,又因为 ,所以 有两解,即 或 .
当 时, ;
当 时, .
本题选择AB选项.
6.(多选题)一艘轮船从A出发,沿南偏东 的方向航行40海里后到达海岛B,然后从B出发,沿北
偏东35°的方向航行了 海里到达海岛C.如果下次航行直接从A出发到C,此船航行的方向和路程
(海里)分别为( )
A.北偏东 B.北偏东 C. D.
【答案】BC
【解析】依题意可得在 中 .
.
由余弦定理可得格致课堂
.
,
由正弦定理可得 ,
由题意可知在 中 为锐角,所以 .
所以如果下次航行直接从A出发到C,此船航行的方向为北偏东 ,路程为
海里.故BC正确.
二、填空题
7.某人站在60米高的楼顶A处测量不可到达的电视塔高,测得塔顶C的仰角为300,塔底B的俯角为
150,已知楼底部D和电视塔的底部B在同一水平面上,则电视塔的高
为 米.
【答案】120+40
【解析】
如图,用AD表示楼高,AE与水平面平行,E在线段BC上,
因为∠CAE=30°,∠BAE=15°,AD=BE=60,
则AE= = =120+60 ,格致课堂
在Rt AEC中,
△
CE=AE·tan30°=(120+60 )× =60+40 ,
∴BC=CE+BE=60+40 +60=(120+40 )米,
所以塔高为(120+40 )米.
8.在O点测量到远处有一物体在做匀速直线运动,开始时刻物体位于P点,一分钟后,其位置在Q点,
且 ,再过一分钟,该物体位于R点,且 ,则 的值是_____________.
【答案】
【解析】由于物体均速直线运动,根据题意, ,不妨设其长度为1.
在 中, , .
在 中,由正弦定理得 ,在 中, ,
两式两边同时相除,得 .
又在 中, ,所以 .
9.如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏
东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变航行的方向继续前进,则此舰
____________触礁的危险.(填“有”或“没有”)
【答案】没有
【解析】
过点B作BD⊥AE交AE于D,由已知,AC=8,∠ABD=75°,∠CBD=60°,格致课堂
在Rt 中,AD=BD·tan∠ABD="BD·tan" 75°,
在Rt 中,CD=BD·tan∠CBD=BD·tan60°,
所以AD-CD=BD(tan75°-tan60°)=AC=8,
所以 ,所以该军舰没有触礁的危险.
10.甲船在岛B的正南A处,AB="10" km,甲船以每小时4 km的速度向正北航行,同时,乙船自B出发
以每小时6 km的速度向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间是
_______h,最近距离是 km.
15√21
【答案】 7
【解析】
根据题意画出示意图,如图,假设t h后甲船行驶到D处,乙船行驶到C处,此时两船相距最近,则
∠DBC=120°,BC=6t,BD=10-4t.在 中,由余弦定理,得CD2=BD2+BC2-
2BD·BCcos∠DBC=(10-4t)2+36t2-2(10-4t)6tcos120°=28t2-20t+100,所以当t= ,即航行时间为 h
√ 5 5 15√21
28×( ) 2 −20× +100=
时,CD2最小,即甲、乙两船相距最近,最近距离为 14 14 7格致课堂
三、解答题
11.如图,在平面直角坐标系 中,已知点A(-3,1),直线OB的倾斜角为45°,且|OB|=.
(1)求点B的坐标及线段AB的长度;
(2)在平面直角坐标系 中,取1厘米为单位长度.现有一质点P以1厘米/秒的速度从点B出发,沿
倾斜角为60°的射线BC运动,另一质点Q同时以厘米/秒的速度从点A出发作直线运动,如果要使得质点
Q与P会合于点C,那么需要经过多少时间?
【解析】:(1)设点B(x,y),
0 0
依题意x=cos 45°=1,y=sin 45°=1,
0 0
从而B(1,1),又A(-3,1),所以AB∥x轴,则|AB|=|1-(-3)|=4.
(2)设质点Q与P经过t秒会合于点C,则AC=t,BC=t.
由AB∥x轴及BC的倾斜角为60°,得∠ABC=120°.
在△ABC中,由余弦定理得AC2=AB2+BC2-2AB·BC·cos 120°,
所以2t2=16+t2+8t·,
化简得t2-4t-16=0,解得t=2-2(舍去)或t=2+2.
即若要使得质点Q与P会合于点C,则需要经过(2+2)秒.
12.如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P(观察站高度忽略不计),上午11时,
测得一轮船在岛北偏东30°方向,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°方向,俯角
为60°的C处.格致课堂
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
【解析】:(1)在Rt PAB中,∠APB=60°,AP=1,
所以AB=APtan 60°△=.
在Rt PAC中,∠APC=30°,
所以△AC=APtan 30°=.
在△ACB中,∠CAB=30°+60°=90°,
所以BC===.
则船的航行速度为÷=2(千米/时).
(2)在△ACD中,∠DAC=90°-60°=30°,sin∠DCA
=sin(180°-∠ACB)=sin∠ACB===,sin∠CDA=sin(∠ACB-30°)
=sin∠ACB·cos 30°-cos∠ACB·sin 30°
=×- =.
由正弦定理得=,
所以AD===.
故此时船距岛A有千米.