文档内容
题 1 2 3 4 5 6 7 8 9 1 1
号 0 1
答 A D A B A D A A A A A
案 C D C
D
12. 13. 14.
15.(1)因为 ,即 ,整理得 ,
解得 或 (舍去),故 . ...................................................4 分
所以 展开式的通项为 (
且 ), ...................................................7 分
则 ,故二项式系数的最大项为第 项,为 ....................7 分
(2)令 ,解得 ,....................9 分
所以 ,
所以二项展开式中含 项的系数为 ;....................13 分
16.(1) ....................5 分
(2)如果男生中的甲和女生中的乙至少要有 人在内,包含两种情况,
第一种甲和乙都在内的选法有 种,
第二种情况,甲乙选 人,有 种选法,
则如果男生中的甲和女生中的乙至少要有 1 人在内,共有 种选法;............10 分
(3)如果 人中必须既有男生又有女生,先从所有 人中选 人,
去掉只有男生和只有女生的情况,故有 种选法.............15 分
17.(1)设事件 为“甲、乙 2 位消费者均抽中三等奖且 2 人最终选择的奖品不
一样”,
答案第 1 页,共 2 页由三等奖有 4 种奖品供选择,故甲、乙 2 位消费者的选择情况共有 (种),
其中 2 人最终选择的奖品不一样的情况有 (种),............3 分
因为每位消费者抽中三等奖的概率均为 ,
所以, .............6 分
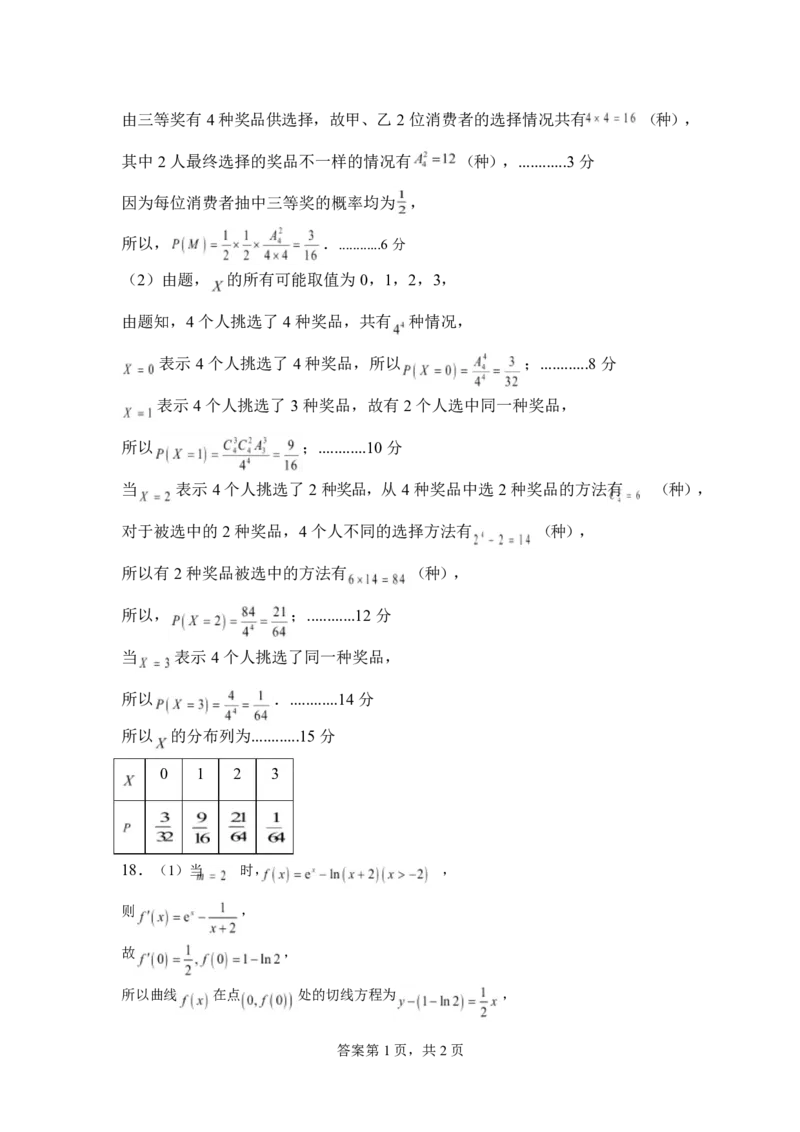
(2)由题, 的所有可能取值为 0,1,2,3,
由题知,4 个人挑选了 4 种奖品,共有 种情况,
表示 4 个人挑选了 4 种奖品,所以 ;............8 分
表示 4 个人挑选了 3 种奖品,故有 2 个人选中同一种奖品,
所以 ;............10 分
当 表示 4 个人挑选了 2 种奖品,从 4 种奖品中选 2 种奖品的方法有 (种),
对于被选中的 2 种奖品,4 个人不同的选择方法有 (种),
所以有 2 种奖品被选中的方法有 (种),
所以, ;............12 分
当 表示 4 个人挑选了同一种奖品,
所以 .............14 分
所以 的分布列为............15 分
0 1 2 3
18.(1)当 时, ,
则 ,
故 ,
所以曲线 在点 处的切线方程为 ,
答案第 1 页,共 2 页即 ;........................................5 分
(2) ,
因为函数 在 处有极值,
所以 ,即 ,解得 ,
此时 ,
因为函数 在 上都是增函数,
所以函数 在 上是增函数,
又 ,
所以 时, ,当 时, ,
所以函数 在 上单调递减,在 上单调递增.......................10 分
(3)法一:令 ,则 ,
当 时, ,当 时, ,
所以函数 在 上单调递减,在 上单调递增,
所以 ,
所以 ,当且仅当 时取等号,.......................13 分
故 ,
令 ,则 ,
当 时, ,当 时, ,
所以函数 在 上单调递减,在 上单调递增,
所以 ,当且仅当 时,等号成立,当 时,
,
所以 ........................17 分
法二:当 m≤2,x∈(-m,+∞)时,ln(x+m)≤ln(x+2),故只需证明当 m=2 时, f(x)>0.
答案第 1 页,共 2 页当 m=2 时,函数 在(-2,+∞)上单调递增........................13 分
又 f '(-1)<0, f '(0)>0,故 f '(x)=0 在(-2,+∞)上有唯一实根 ,且 .
当 时, f '(x)<0;当 时, f '(x)>0,从而当 时,f(x)取得最小
值.
由 f '(x )=0 得 = , ,
0
故 .
综上,当 m≤2 时, f(x)>0........................17 分
19.(1)由 ,求导可得 ,令 ,解得
且 m≠0.
由函数 为“ 函数”,则 ,
可得 ,解得 ........................5 分
(2)①由 ,则 ,求导可得 ,令
,
由题意可得函数 存在两个不同的变号零点,则 ,
令 ,解得 ,当 时, ,则 在 上单调递减;
当 时, ,则 在 上单调递增,所以 ,
由 ,令 ,.......................8 分
求导可得 ,令 ,解得 ,
当 时, ,则 在 上单调递减;
当 时, ,则 在 上单调递增,
所以 ,则 ,
答案第 1 页,共 2 页由 ,则当 时,函数 存在两个不同的变号零点,
可得 ,解得 ........................11 分
②由①可得 ,易知方程 存在两个不相等的实数根,
设为 ,由①不妨设 ,
令 ,
求导可得 ,由 ,当且仅当 时取等号,则 ,
所以函数 在 上单调递增,由 ,则当 时 ,可得
,
由 ,且函数 在 上单调递减,则 ,可得
;
由当 时, ,则函数 在 上单调递减,
由 ,则 ,所以 ,
要证 ,只需证 ,
由 ,则令 ,......................14 分
求导可得 ,令 ,则 ,
所以函数 在 上单调递增,则当 时, ,即 ,
所以函数 在 上单调递增,则当 时, ,
所以不等式 在 上恒成立,可得 ,
综上所述, ,所以函数 为“ 函数”......................17 分
答案第 1 页,共 2 页