文档内容
http://t.cn/Ri466E4
苏教版六年级(上)期中数学试卷(3)
一、想一想、填一填
1.食堂原有600千克面粉,吃掉a袋,每袋80千克,还剩 千克.
2.超市运来苹果X千克,是运来香蕉的3倍,运来香蕉 千克;运来的梨比苹
果的 少20千克,运来梨 千克.
3.一个长方体的长、宽、高分别是10厘米、5厘米、8厘米.这个长方体的表面积是
平方厘米.
4.用一根长96厘米的铁丝正好做成一个正方体,这个正方体的体积是 立方
厘米.
5.
1
4 1
4
5 .
5
0 2
0
d 升
克
m=
=
=
毫
千
m升
克
3
8
1
0
.
1 立
5
8 方
立
分厘
方
= 米
分
=
米
小
=
时立
方
升
分
米
6.0.125的倒数是 ,1的倒数是 .
7.1吨菜籽可以榨油 吨,140吨菜籽可以榨油 吨;要榨140吨油需大豆
吨.
8. × = ÷ = ﹣ = .
9.食堂中午准备午餐,买来萝卜x千克,鸭子重量比萝卜重量的2倍少10千克,买来鸭
子 千克,如果鸭子是290千克,那么萝卜有 千克.
10.甲数是720,乙数是甲数的 ,丙数是乙数的 倍,丙数是 .
11.把一根长3米的长方体木料,平均锯成三段,表面积增加了2.4平方米,这根木料的体
积是 立方米.
12.把45立方分米的水倒入长5分米,宽3分米,高4分米的鱼缸内,水面距缸边还有
分米.
教育 1http://t.cn/Ri466E4
二、慎思妙断
13.9x=0,这个方程没有解. .(判断对错)
14.把一个正方体橡皮泥捏成一个长方体,它的形状变了,体积不变. .
(判断对错)
15.一个非0数除以 ,相当于把这个数扩大3倍. .(判断对错)
16.体积相等的两个正方体,它们的表面积一定相等. .(判断对错)
17.如果A是B的 ,那么B是A的 倍. .(判断对错)
三、精挑细选
18.比80的 少8的数是( )
A.13 B.16 C.7 D.23
19.两根同样长的铁丝,一根用去了 ,另一根用去了 米,剩下的铁丝相比,( )
A.第一根长B.第二根长
C.同样长 D.无法比较哪根长
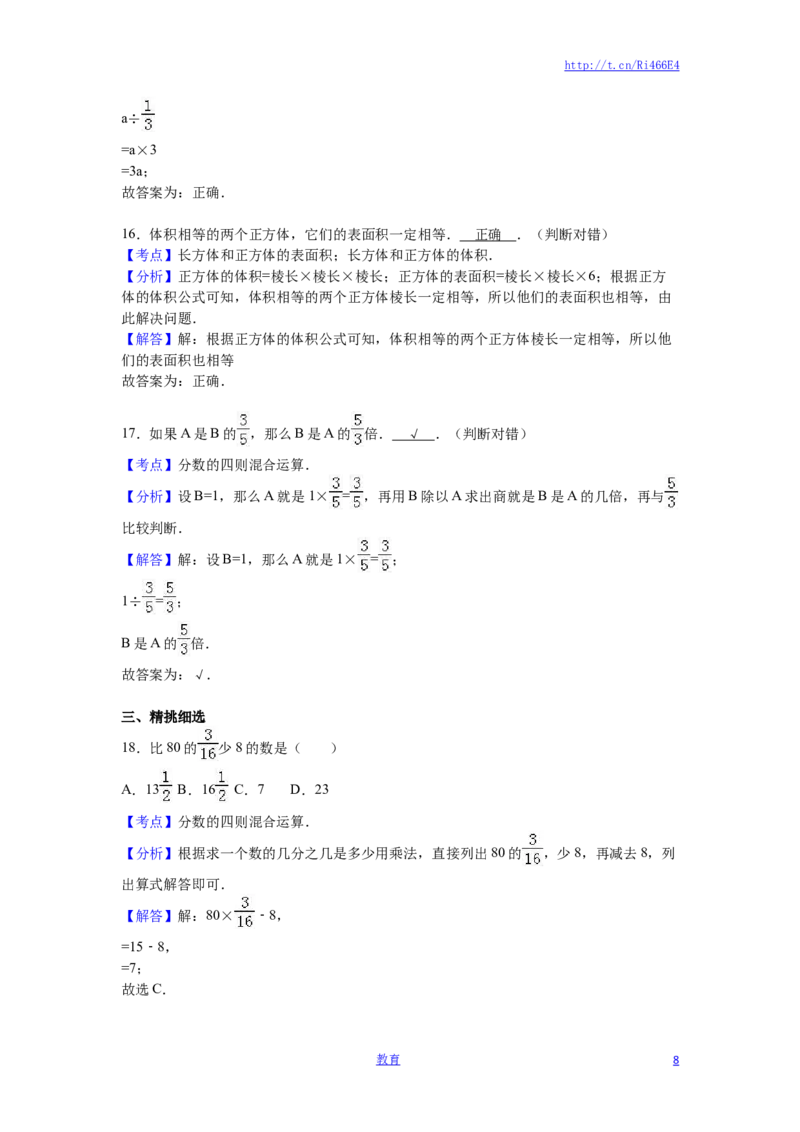
20.图是一个长3厘米、宽和高都是2厘米的长方体.将它挖掉一个棱长1厘米的小正方
形,它的表面积( )
A.比原来大B.比原来小 C.不变 D.无法确定
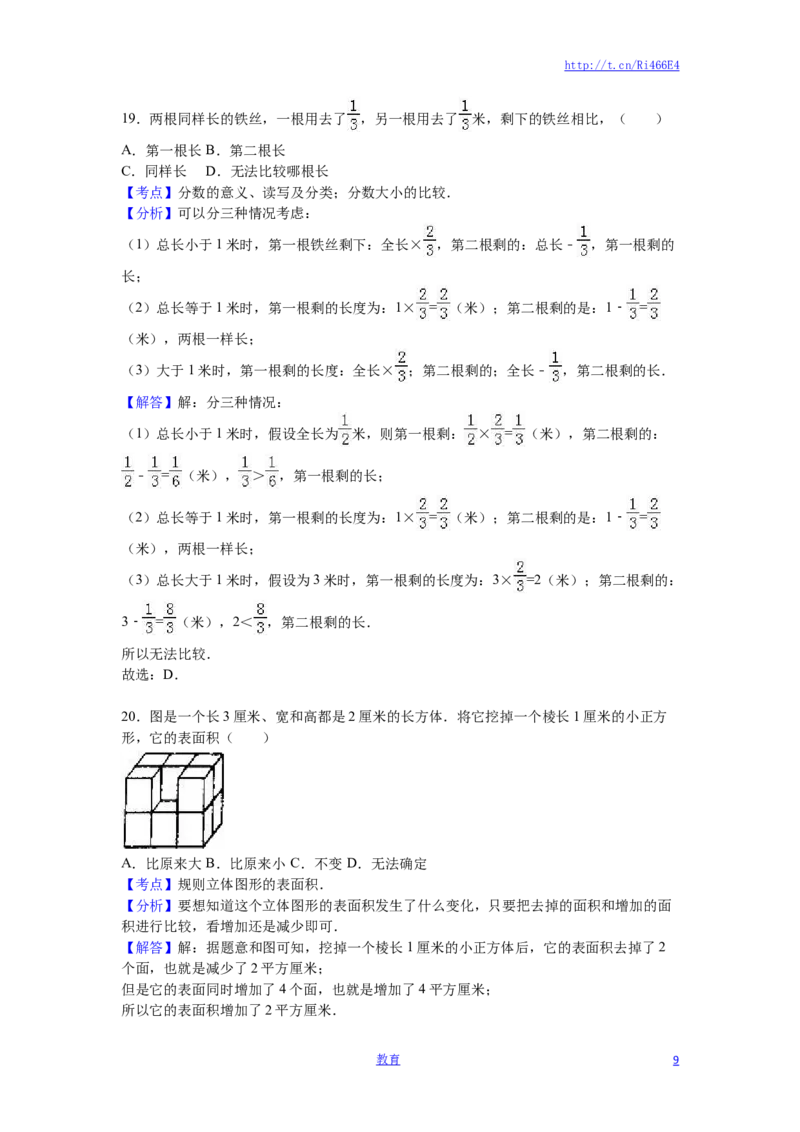
21.下面能折成正方体的是( )
A. B. C. D.
22.小明今年m岁,小刚今年(m+4)岁,5年后,他们相差( )岁.
A.4 B.5 C.m+5 D.9
23.一个长方体的长、宽、高都乘2,体积就乘( )
A.2 B.4 C.6 D.8
24.把棱长是5厘米的两个正方体拼成一个长方体,长方体的表面积比两个正方体表面积
之和减少了( )平方厘米.
A.50 B.25 C.10 D.5
四、计算园地.
25.
教育 2http://t.cn/Ri466E4
直接写得数.
1÷ ﹣
﹣ = ÷ =
× =
= =
8÷ = + = ×0= 2× = ÷8=
26.
计算
① + ﹣ ②25× × ③ × ×
④ ⑤ ⑥ .
27.解方程.
9.5x﹣5.3x=12.6 5x﹣4.2=8.8 18x÷(45﹣9)=4 6x+5×4.4=40.
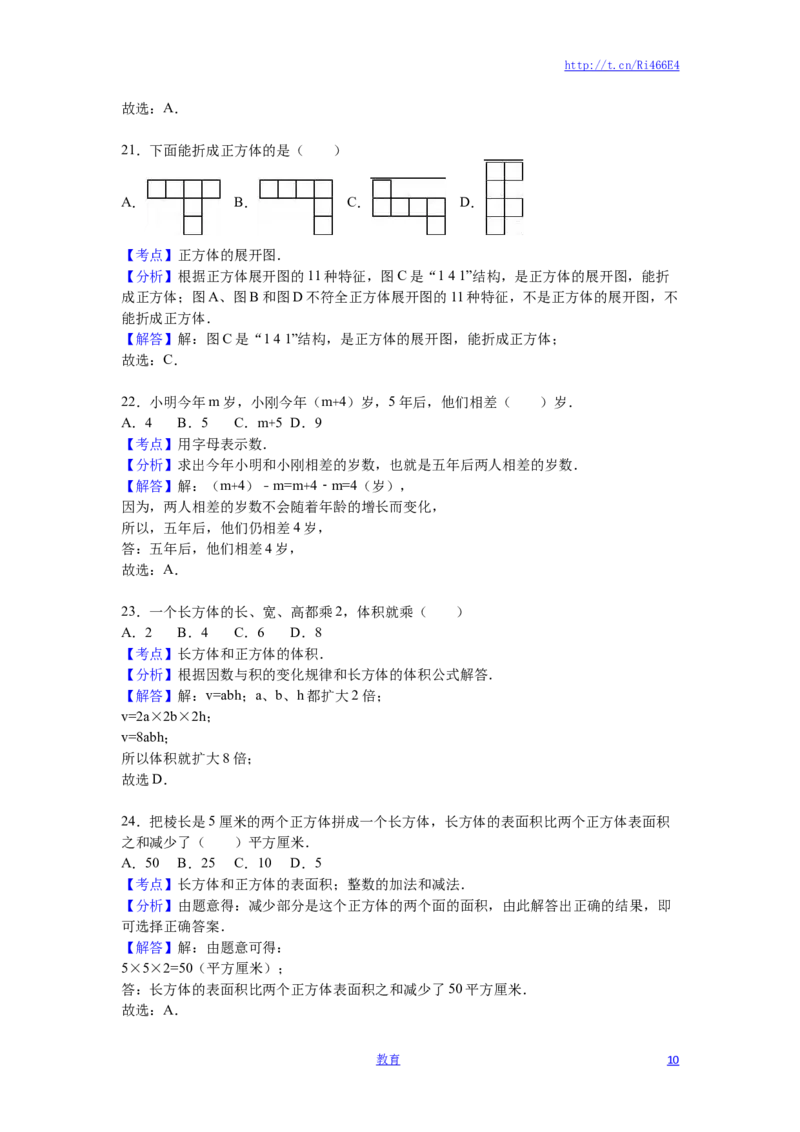
28.求下列各题中x的值.
五、解决问题.(26分,1--5每题4分,第6题每小题4分)
29.商店运来一批冰箱共150台,已经售出 .售出冰箱多少台?
30.六年级参加数学兴趣小组的有12人,占全班人数的 .六年级共有多少名学生?
31.小芳骑自行车每小时12千米,小芳骑自行车每小时行的比汽车每小时行的 少6千米.
汽车每小时行多少千米?[方程解].
32.一列火车 小时行90千米,照这样计算,从甲地到乙地要行 小时,甲、乙两地铁路
长多少千米?
33.一节长方体通风管(如图),长3分米,宽2分米,高1.5分米,做3节这样的通风管
需要多少平方分米铁皮?
34.建一个长50米、宽40米、深2米的游泳池.
(1)这个游泳池最多能装水多少立方米?
(2)如果在游泳池的四壁和底部抹水泥,抹水泥部分的面积是多少平方米?
教育 3http://t.cn/Ri466E4
苏教版六年级(上)期中数学试卷(3)
参考答案与试题解析
一、想一想、填一填
1.食堂原有600千克面粉,吃掉a袋,每袋80千克,还剩 600﹣80 a 千克.
【考点】用字母表示数.
【分析】用“80×a”求出吃掉多少千克,然后用原有的千克数﹣吃掉的千克数=剩下的千克
数,据此解答即可.
【解答】解:600﹣80×a=600﹣80a(千克)
答:还剩 600﹣80a千克.
故答案为:600﹣80a.
2.超市运来苹果X千克,是运来香蕉的3倍,运来香蕉 X÷ 3 或 千克;运来的梨比苹
果的 少20千克,运来梨 x﹣20 千克.
【考点】用字母表示数.
【分析】由所给条件可知:香蕉的3倍是苹果的X千克,求香蕉的质量,用除法计算;梨
比苹果的 少20千克,求梨的质量,就是求比x的 少20千克的数是多少.
【解答】解:香蕉:x÷3或 ;
梨:x× ﹣20= x﹣20.
故答案为:X÷3或 , x﹣20.
3.一个长方体的长、宽、高分别是10厘米、5厘米、8厘米.这个长方体的表面积是
340 平方厘米.
【考点】长方体和正方体的表面积;长方体的特征.
【分析】要求长方体的表面积,根据“长方体的表面积=(长×宽+长×高+宽×高)×2”,
代入数值,进行解答即可;
【解答】解:(10×5+10×8+5×8)×2,
=170×2,
=340(平方厘米);
故答案为:340.
4.用一根长96厘米的铁丝正好做成一个正方体,这个正方体的体积是 51 2 立方厘米.
【考点】长方体和正方体的体积;正方体的特征.
【分析】由于正方体的12条棱的长度都相等,已知棱长总和是96厘米,先求出正方体的
棱长,再利用正方体的体积公式解答.
【解答】解:96÷12=8(厘米);
教育 4http://t.cn/Ri466E4
8×8×8=512(立方厘米);
答:这个正方体的体积是512立方厘米.
故答案为:512.
5.
450dm= 4 5 m 1.2升= 120 0 毫升 1450克= 1.4 5 千克
18分= 0. 3 小时 380立方厘米= 0.3 8 立方分米 1.5立方分米= 1. 5 升
【考点】长度的单位换算;质量的单位换算;体积、容积进率及单位换算.
【分析】(1)低级单位分米化高级单位米除以进率10.
(2)高级单位升化低级单位毫升乘进率1000.
(3)低级单位克化高级单位千克除以进率1000.
(4)低级单位分化高级单位小时除以进率60.
(5)低级单位立方厘米化高级单位立方分米除以进率1000.
(6)立方分米与升是等量关系二者互化数值不变.
【解答】解:(1)450dm=45m;
(2)1.2升=1200毫升;
(3)1450克=1.45千克;
(4)18分=0.3小时;
(5)380立方厘米=0.38立方分米;
(6)1.5立方分米=1.5升.
故答案为:45,1200,1.45,0.3,0.38,1.5.
6.0.125的倒数是 8 ,1的倒数是 1 .
【考点】倒数的认识.
【分析】先把小数化为分数,再运用倒数的求法解答.
【解答】解:0.125= ,
的倒数为1÷ =8;
1的倒数是1.
故答案为:8,1.
7.1吨菜籽可以榨油 吨,140吨菜籽可以榨油 4 9 吨;要榨140吨油需大豆 40 0
吨.
【考点】分数乘法应用题;分数除法应用题.
【分析】根据:“1吨菜籽可以榨油 吨,”知道1吨菜籽可以榨油多少吨,或求出榨一
吨油需要多少吨菜籽,根据乘法的意义,即可列式求出答案.
【解答】解:(1)140× =49(吨)
(2)1÷ ×140=400(吨)
答:140吨菜籽可以榨油 49吨;要榨140吨油需大豆400吨.
故答案是:49,400.
教育 5http://t.cn/Ri466E4
8. × = ÷ = ﹣ = .
【考点】分数的加法和减法;分数乘法;分数除法.
【分析】取特殊值,令等式结果为1,即可求出结果.
【解答】解: × = ÷ = ﹣ = .
故答案为: , , , .
9.食堂中午准备午餐,买来萝卜x千克,鸭子重量比萝卜重量的2倍少10千克,买来鸭
子 2x﹣1 0 千克,如果鸭子是290千克,那么萝卜有 15 0 千克.
【考点】整数、小数复合应用题;用字母表示数;含字母式子的求值.
【分析】(1)先求出萝卜重量的2倍,然后减去10,即2x﹣10千克;
(2)由题意可得:2x﹣10=290,然后解答即可.
【解答】解:(1)x×2﹣10=2x﹣10;
(2)2x﹣10=290,
x=150;
答:买来鸭子2x﹣10千克,萝卜有150千克.
故答案为:2x﹣10,150.
10.甲数是720,乙数是甲数的 ,丙数是乙数的 倍,丙数是 16 0 .
【考点】分数乘法应用题.
【分析】根据“乙数是甲数的 ”,把甲数看做单位“1”,单位“1”的量是已知的,求乙
数,用乘法计算;再根据“丙数是乙数的 倍”,把乙数看做单位“1”,单位“1”的量是
已知的,求丙数,用乘法计算.
【解答】解:乙数:720× =120;
丙数:120× =160;
答:丙数是160.
故答案为:160.
11.把一根长3米的长方体木料,平均锯成三段,表面积增加了2.4平方米,这根木料的体
积是 1. 8 立方米.
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【分析】把一根长3米的长方体木料,平均锯成三段,需要锯3﹣1=2次,表面积增加了
2×2=4个横截面的面积,用增加的表面积除以4,求出横截面的面积;然后根据这根木料
的体积=横截面的面积×长,求出这根木料的体积是多少即可.
【解答】解:把长方体木料平均锯成三段,需要锯的次数是:
3﹣1=2(次)
教育 6http://t.cn/Ri466E4
[2.4÷(2×2)]×3
=[2.4÷4]×3
=0.6×3
=1.8(立方米)
答:这根木料的体积是1.8立方米.
故答案为:1.8.
12.把45立方分米的水倒入长5分米,宽3分米,高4分米的鱼缸内,水面距缸边还有
1 分米.
【考点】长方体和正方体的体积.
【分析】因为水的体积是不变的,用水的体积除以鱼缸的底面积求出水在鱼缸内的高度,
然后和鱼缸的高相减即可.
【解答】解:4﹣45÷(5×3),
=4﹣45÷15,
=4﹣3,
=1(分米).
答:水面距缸边还有1分米.
故答案为:1.
二、慎思妙断
13.9x=0,这个方程没有解. 错误 .(判断对错)
【考点】方程的解和解方程.
【分析】先确定9X=0是方程,根据等式的基本性质,求出方程的解即可..
【解答】解:9x=0,
x=0÷9,
x=0;
所以这个方程的解是0;
故答案为:错误.
14.把一个正方体橡皮泥捏成一个长方体,它的形状变了,体积不变. 正确 .(判断
对错)
【考点】体积、容积及其单位.
【分析】物体的体积是指:物体所占空间的大小.把一块橡皮泥无论捏成一个正方体还是
一个长方体,它的形状虽然变了,但是所占空间的大小没变,即体积不变.
【解答】解:把一个正方体橡皮泥捏成一个长方体,它的形状变了,体积不变.
故答案为:正确.
15.一个非0数除以 ,相当于把这个数扩大3倍. 正确 .(判断对错)
【考点】分数除法.
【分析】一个非0数除以 ,就等于乘以 的倒数3,相当于把这个数扩大3倍.
【解答】解:a为一个非0的数
教育 7http://t.cn/Ri466E4
a÷
=a×3
=3a;
故答案为:正确.
16.体积相等的两个正方体,它们的表面积一定相等. 正确 .(判断对错)
【考点】长方体和正方体的表面积;长方体和正方体的体积.
【分析】正方体的体积=棱长×棱长×棱长;正方体的表面积=棱长×棱长×6;根据正方
体的体积公式可知,体积相等的两个正方体棱长一定相等,所以他们的表面积也相等,由
此解决问题.
【解答】解:根据正方体的体积公式可知,体积相等的两个正方体棱长一定相等,所以他
们的表面积也相等
故答案为:正确.
17.如果A是B的 ,那么B是A的 倍. √ .(判断对错)
【考点】分数的四则混合运算.
【分析】设B=1,那么A就是1× = ,再用B除以A求出商就是B是A的几倍,再与
比较判断.
【解答】解:设B=1,那么A就是1× = ;
1÷ = ;
B是A的 倍.
故答案为:√.
三、精挑细选
18.比80的 少8的数是( )
A.13 B.16 C.7 D.23
【考点】分数的四则混合运算.
【分析】根据求一个数的几分之几是多少用乘法,直接列出80的 ,少8,再减去8,列
出算式解答即可.
【解答】解:80× ﹣8,
=15﹣8,
=7;
故选C.
教育 8http://t.cn/Ri466E4
19.两根同样长的铁丝,一根用去了 ,另一根用去了 米,剩下的铁丝相比,( )
A.第一根长B.第二根长
C.同样长 D.无法比较哪根长
【考点】分数的意义、读写及分类;分数大小的比较.
【分析】可以分三种情况考虑:
(1)总长小于1米时,第一根铁丝剩下:全长× ,第二根剩的:总长﹣ ,第一根剩的
长;
(2)总长等于1米时,第一根剩的长度为:1× = (米);第二根剩的是:1﹣ =
(米),两根一样长;
(3)大于1米时,第一根剩的长度:全长× ;第二根剩的;全长﹣ ,第二根剩的长.
【解答】解:分三种情况:
(1)总长小于1米时,假设全长为 米,则第一根剩: × = (米),第二根剩的:
﹣ = (米), > ,第一根剩的长;
(2)总长等于1米时,第一根剩的长度为:1× = (米);第二根剩的是:1﹣ =
(米),两根一样长;
(3)总长大于1米时,假设为3米时,第一根剩的长度为:3× =2(米);第二根剩的:
3﹣ = (米),2< ,第二根剩的长.
所以无法比较.
故选:D.
20.图是一个长3厘米、宽和高都是2厘米的长方体.将它挖掉一个棱长1厘米的小正方
形,它的表面积( )
A.比原来大B.比原来小 C.不变 D.无法确定
【考点】规则立体图形的表面积.
【分析】要想知道这个立体图形的表面积发生了什么变化,只要把去掉的面积和增加的面
积进行比较,看增加还是减少即可.
【解答】解:据题意和图可知,挖掉一个棱长1厘米的小正方体后,它的表面积去掉了2
个面,也就是减少了2平方厘米;
但是它的表面同时增加了4个面,也就是增加了4平方厘米;
所以它的表面积增加了2平方厘米.
教育 9http://t.cn/Ri466E4
故选:A.
21.下面能折成正方体的是( )
A. B. C. D.
【考点】正方体的展开图.
【分析】根据正方体展开图的11种特征,图C是“1 4 1”结构,是正方体的展开图,能折
成正方体;图A、图B和图D不符全正方体展开图的11种特征,不是正方体的展开图,不
能折成正方体.
【解答】解:图C是“1 4 1”结构,是正方体的展开图,能折成正方体;
故选:C.
22.小明今年m岁,小刚今年(m+4)岁,5年后,他们相差( )岁.
A.4 B.5 C.m+5 D.9
【考点】用字母表示数.
【分析】求出今年小明和小刚相差的岁数,也就是五年后两人相差的岁数.
【解答】解:(m+4)﹣m=m+4﹣m=4(岁),
因为,两人相差的岁数不会随着年龄的增长而变化,
所以,五年后,他们仍相差4岁,
答:五年后,他们相差4岁,
故选:A.
23.一个长方体的长、宽、高都乘2,体积就乘( )
A.2 B.4 C.6 D.8
【考点】长方体和正方体的体积.
【分析】根据因数与积的变化规律和长方体的体积公式解答.
【解答】解:v=abh;a、b、h都扩大2倍;
v=2a×2b×2h;
v=8abh;
所以体积就扩大8倍;
故选D.
24.把棱长是5厘米的两个正方体拼成一个长方体,长方体的表面积比两个正方体表面积
之和减少了( )平方厘米.
A.50 B.25 C.10 D.5
【考点】长方体和正方体的表面积;整数的加法和减法.
【分析】由题意得:减少部分是这个正方体的两个面的面积,由此解答出正确的结果,即
可选择正确答案.
【解答】解:由题意可得:
5×5×2=50(平方厘米);
答:长方体的表面积比两个正方体表面积之和减少了50平方厘米.
故选:A.
教育 10http://t.cn/Ri466E4
四、计算园地.
25.
直接写得数.
1÷ ÷ ﹣
﹣ =
× =
= = =
×0
8÷ = + = 2× = ÷8=
=
【考点】分数的加法和减法;分数乘法;分数除法.
【分析】分数乘法:分子相乘的积做分子,分母相乘的积做分母;
分数除法:除以一个不为零的数等于乘上这个数的倒数;
异分母分数相加减,先通分,化成同分母的分数,再计算.
【解答】解:
× = 1÷ = ﹣ = ÷ = ﹣ =
8÷ =12 + = ×0=0 2× = ÷8=
26.
计算
① + ﹣ ②25× × ③ × ×
④ ⑤ ⑥ .
【考点】分数的四则混合运算.
【分析】①通分计算;
②③约分计算;
④⑤⑥把除法改为乘法,约分计算.
【解答】解:① + ﹣ ,
= + ﹣ ,
= ;
②25× × = ;
③ × × = ;
④ ÷6÷
= × ×15,
教育 11http://t.cn/Ri466E4
= ;
⑤ × ÷ ,
= × × ,
= ;
⑥15÷ × ,
=15× × ,
= .
27.解方程.
9.5x﹣5.3x=12.6 5x﹣4.2=8.8 18x÷(45﹣9)=4 6x+5×4.4=40.
【考点】方程的解和解方程.
【分析】①9.5x﹣5.3x=12.6利用乘法的分配律变成x(9.5﹣5.3)=12.6,4.2x=12.6,利用
等式的性质方程的两边同时除以4.2即可;
②5x﹣4.2=8.8利用等式的性质方程的两边同时加上4.2,再除以5即可;
③18x÷(45﹣9)=4先算出45﹣9=36,利用等式的性质方程的两边同时乘36,再除以18
即可;
④6x+5×4.4=40先算出5×4.4=22,利用等式的性质方程的两边同时减去22,再除以6即可.
【解答】解:①9.5x﹣5.3x=12.6,
x(9.5﹣5.3)=12.6,
4.2x=12.6,
4.2x÷4.2=12.6÷4.2,
x=3;
②5x﹣4.2=8.8,
5x﹣4.2+4.2=8.8+4.2,
5x=13,
5x÷5=13÷5,
x=2.6;
③18x÷(45﹣9)=4,
18x÷36=4,
18x÷36×36=4×36,
18x=144,
18x÷18=144÷18,
x=8;
教育 12http://t.cn/Ri466E4
④6x+5×4.4=40,
6x+22=40,
6x+22﹣22=40﹣22,
6x=18,
6x÷6=18÷6,
x=3.
28.求下列各题中x的值.
【考点】方程的解和解方程.
【分析】(1)根据线段图,甲是x,乙是甲的3倍多19,那么乙是3x+19,正好等于82,
由此列出等式3x+19=82,解答即可;
(2)设长方体的高为x厘米,根据长方体体积公式列出方程5×4×x=50,解方程即可.
【解答】解:(1)设甲数为x,由题意得:
3x+19=82,
3x+19﹣19=82﹣19,
3x=63,
3x÷3=63÷3,
x=21;
(2)设长方体的高为x厘米,得:
5×4×x=50,
20x=50,
20x÷20=50÷20,
x=2.5.
五、解决问题.(26分,1--5每题4分,第6题每小题4分)
29.商店运来一批冰箱共150台,已经售出 .售出冰箱多少台?
【考点】分数乘法应用题.
【分析】要求售出冰箱多少台?要看售出了谁的 ,判断出单位“1”,把这批冰箱的总台
数看作单位“1”,售出了150的 ,根据一个数乘分数的意义,用乘法计算得出.
【解答】解:150× =125(台) 答:售出冰箱125台.
教育 13http://t.cn/Ri466E4
30.六年级参加数学兴趣小组的有12人,占全班人数的 .六年级共有多少名学生?
【考点】分数除法应用题.
【分析】根据“占全班人数的 .”知道单位“1”是全班的人数,即是所要求的结果,根
据已知一个数的几分之几是多少,求这个数,用除法解答即可.
【解答】解:12 =48(人)
答:六年级共有48名学生.
31.小芳骑自行车每小时12千米,小芳骑自行车每小时行的比汽车每小时行的 少6千米.
汽车每小时行多少千米?[方程解].
【考点】分数除法应用题.
【分析】设汽车每小时行驶的路程是x千米,并把它看成单位“1”,它的 就是 x千米,
再根据 x减去6千米就是12千米列出方程求解.
【解答】解:设汽车每小时行驶的路程是x千米,由题意得:
x﹣6=12,
x=18,
x=81;
答:汽车每小时行81千米.
32.一列火车 小时行90千米,照这样计算,从甲地到乙地要行 小时,甲、乙两地铁路
长多少千米?
【考点】简单的归一应用题.
【分析】照这样计算,说明速度不变,先根据 小时行驶的路程求出速度,再由速度和行
驶的时间求出路程.
【解答】解:90 × ,
=120× ,
=540(千米);
答:甲、乙两地铁路长540千米.
33.一节长方体通风管(如图),长3分米,宽2分米,高1.5分米,做3节这样的通风管
需要多少平方分米铁皮?
教育 14http://t.cn/Ri466E4
【考点】长方体、正方体表面积与体积计算的应用.
【分析】首先搞清这道题是求长方体的表面积,其次这个长方体的表面由四个长方形组成,
缺少左右两个面;只求它的前后、上下4个面的面积之和;再乘3由此列式解答.
【解答】解:(3×2+3×1.5)×2×3,
=(6+4.5)×2×3,
=10.5×2×3,
=21×3,
=63(平方分米);
答:做3节这样的通风管需要63平方分米铁皮.
34.建一个长50米、宽40米、深2米的游泳池.
(1)这个游泳池最多能装水多少立方米?
(2)如果在游泳池的四壁和底部抹水泥,抹水泥部分的面积是多少平方米?
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【分析】(1)利用V=sh求出体积即可;
(2)抹水泥部分共有5个面,利用表面积公式(无盖)列式解答即可.
【解答】解:(1)50×40×2=4000(立方米);
(2)50×2×2+40×2×2+50×40,
=200+160+2000,
=2360(平方米);
答:这个游泳池最多能装水4000立方米,抹水泥部分的面积是2360平方米.
教育 15http://t.cn/Ri466E4
2016年8月17日
教育 16