江西省泰和中学2024届高三暑期质量检测数学(1)_2023年7月_027月合集_2024届江西省泰和中学高三暑期质量检测

泰和中学 2024 届高三暑期质量检测数学试卷
一、单选题（共 40分）
1.已知集合A 1，2，3，4，5，6  ，B  2，3  ，C  2，4，6  ，则 ð B  C （ ）
A
A.  2，4，6  B.  1，3，4，5，6  C.  4，6  D.  2 
2.已知事件A，B满足P  A   0.7，P  B   0.6，P  AB   0.42，则P  B A  的值是（ ）
A.0.7 B.0.42 C.0.5 D.0.6
S
3.设等比数列 a 的前n项和为S ，且a 3a ，则 12 （ ）
n n 8 11 S
6
8 9 10 9
A. B. C. D.
9 10 9 8
4.已知定义在R上的函数 f  x 满足 f  x2  f  x ，且当x 0，2 时， f  x   log  x1 ，则
2
f  47  （ ）
A.2 B.0 C.1 D.-1
 
5.已知 f x 1  x3，则 f  x 的解析式为（ ）
A.x4  x  0  B.x2 3  x  0 
C.x2 2x4  x 1  D.x2 3  x 1 
x
b
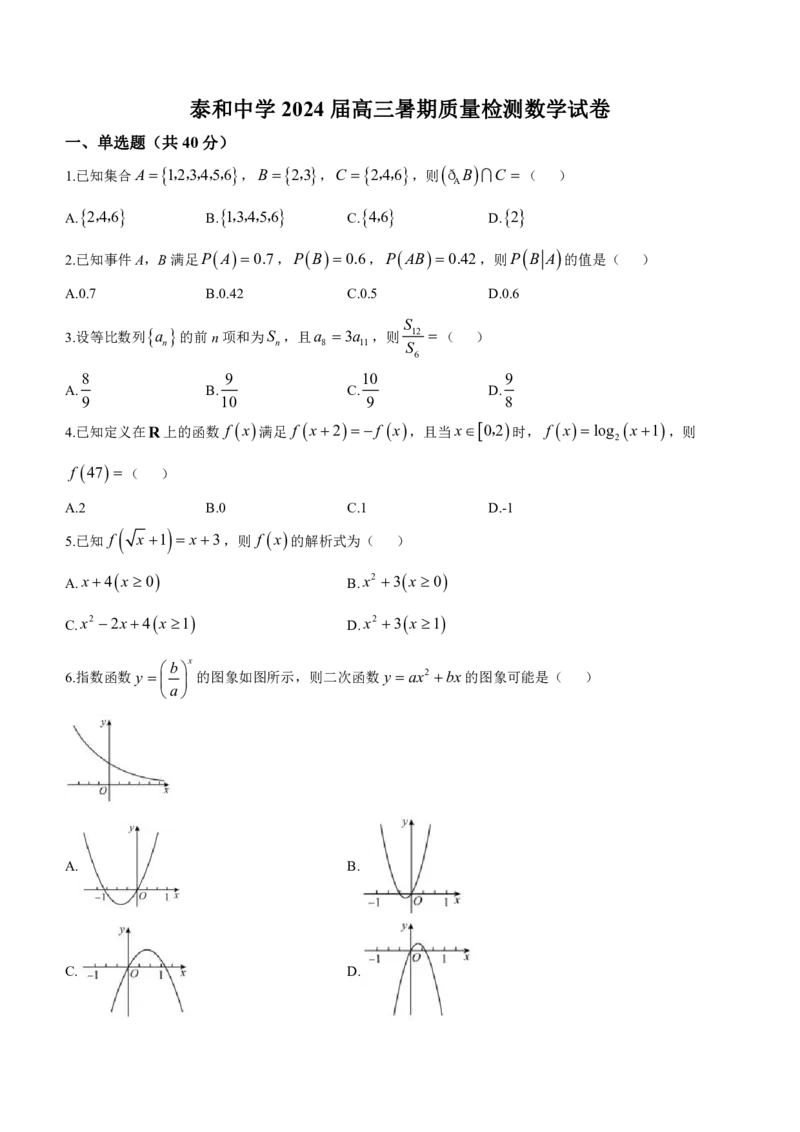
6.指数函数 y    的图象如图所示，则二次函数 y  ax2 bx的图象可能是（ ）
a
A. B.
C. D.
学科网（北京）股份有限公司1
7.若直线 y  kxn与曲线y  lnx 相切，则实数k的取值范围是（ ）
x
 1 1 
A.
，
 B.
 4，
C.
4，
D.
，

 4 4 
 xk  1a2  ，x  0

8.已知 f  x    ，aR ，对任意非零实数x ，存在唯一的非零实数x  x  x ，
x2 4x 3a 2，x  0 1 2 1 2

使得 f  x   f  x 成立，则实数k的取值范围是（ ）
1 2
A.k 0 B.k 8 C.0 k 8 D.k 0或k 8
二、多选题（共 20分）
9.下列求导运算正确的是（ ）

   3 1 3
A. ex ex B. lnx

 
 x x x2

C. 

sinx

 xcosx sinx D.  3xsin2x  3x  ln3sin2x2cos2x 
 x  x2
x2，2 x 1，
10.已知函数 f  x    关于函数 f  x 的结论正确的是( )
x2，x 1，
A. f  x 的定义域为R B. f  x 的值域为，4 
C.若 f  x   2，则x的值是 2 D. f  x 1的解集为1，1 
11.下列说法中，正确的有（ ）
A.已知a a 2，则数列 a 是递减数列
n1 n n
B.数列 a 的通项a  n2 kn 2，若 a 为单调递增数列，则k 3
n n n
C.已知正项等比数列 a ，则有a a  a a
n 1 8 4 5
D.已知等差数列 a 的前n项和为S ，S  4，S 10，则S 18
n n 2 4 6
12.已知a，b为正实数，且ab2ab 16，则（ ）
A.ab的最大值为8 B.2ab的最小值为8
1 1 2
C.ab的最小值为6 2 3 D.  的最小值为
a1 b2 2
三、填空题（共 20分）
13.已知随机变量X服从两点分布，且P  X  0  2a ，P  X 1 a，那么a  _______________.
学科网（北京）股份有限公司14.函数 y  x x1的最小值为_______________.
15.已知nN*，将数列 2n1 与数列  n2 1  的公共项从小到大排列得到新数列 a ，则
n
1 1 1
  
_______________.
a a a
1 2 10
 x1  ex，x  0

16.已知函数 f  x    lnx ，函数g  x    f  x 2    f  x a  ，若函数g  x 恰有三个零点，
 ，x  0
 x
则a的取值范围是_______________.
四、解答题（共 70分）
17.某骑行爱好者近段时间在专业人士指导下对骑行情况进行了统计，各次骑行期间的身体综合指标评分x与
对应用时y（单位：小时）如下表：
身体综合指标评分（x） 1 2 3 4 5
用时（y/小时） 9.5 8.6 7.8 7 6.1
（1）由上表数据看出，可用线性回归模型拟合y与x的关系，请用相关系数加以说明；
（2）建立y关于x的回归方程.
n  x x  y  y  n  x x  y  y 
参考数据和参考公式：相关系数r  i1 i i ，b   i1 i i ，
n  x x 2n  y  y 2 n  x x 2
i1 i i1 i i1 i
aˆ  y b ˆ x ， 7060 84
18.已知等差数列 a 的前n项和为S ，且a  11，S  S .
n n 5 3 17
（1）求
a
的通项公式；
n
（2）试求出所有的正整数m，使得对任意正整数n，均有S  S 1.
m n
1
19.已知函数 f  x   x2 ax2lnx  aR  .
2
（1）当a 1时，求函数 f  x 的极值；
（2）若函数 f  x 在区间  1，上单调递增，求实数a的取值范围.
a
20.记S 为数列 a 的前n项和，已知S  n n2 1，nN*.
n n n 2
（1）求a a ，并证明 a a 是等差数列；
1 2 n n1
（2）求S .
n
学科网（北京）股份有限公司21.2023年2月2日，第27个世界湿地日中国主场宣传活动在杭州西溪国家湿地公园举行，2023年世界湿地
日将主题定为“湿地修复”.某校为增强学生保护生态环境的意识，举行了以“要像保护眼睛一样保护自然和
生态环境”为主题的知识竞赛，比赛分为三轮，每轮先朗诵一段爱护环境知识，再答3道试题，每答错一道题，
3
用时额外加20秒，最终规定用时最少者获胜，已知甲、乙两人参加比赛，甲每道试题答对的概率均为 ，乙
5
2
每道试题答对的概率均为 ，甲每轮朗诵的时间均比乙少10秒，假设甲、乙两人答题用时相同，且每道试题
3
是谁答对互不影响.
（1）若甲、乙两人在第一轮和第二轮答对的试题的总数量相同，求乙最终获胜的概率；
（2）请用统计学的知识解释甲和乙谁获胜的可能性更大.
ex
22.已知函数 f  x   lnxxa.
x
（1）若 f

x

0，求a的取值范围；
（2）证明：若 f  x  有两个零点x ，x ，则x x 1.
1 2 1 2
学科网（北京）股份有限公司学科网（北京）股份有限公司