文档内容
高二物理参考答案
1.C 2.B 3.D 4.A 5.B 6.D 7.D 8.C 9.AC 10.AD 11.AD 12.BCD
13.(2)左 左 (3)A 断开开关
14. (1)A (2)C
(3)①变压器原副线圈的电压之比等于匝数之比 ②有漏磁、铁芯发热、导线发
热等(分析其中一个合理因素均给分)
15.(1)感应电动势的最大值 -----2 分
从线框转至中性面位置开始计时,线圈中感应电动势的表达式为
-----2 分
(2)感应电动势的有效值为 -----1 分
线圈内电压 U
内
=Ir=40V-----1 分
电压表的示数 U=E﹣U
内
=200V﹣40V=160V-----1 分
由于是理想变压器 P =P
入 出
电阻 R 上消耗的电功率 P=UI=640W-----1 分
根据变压比可知,电阻 R 两端的电压 U
R
= =80V-----1 分
电阻 R= =10Ω-----1 分
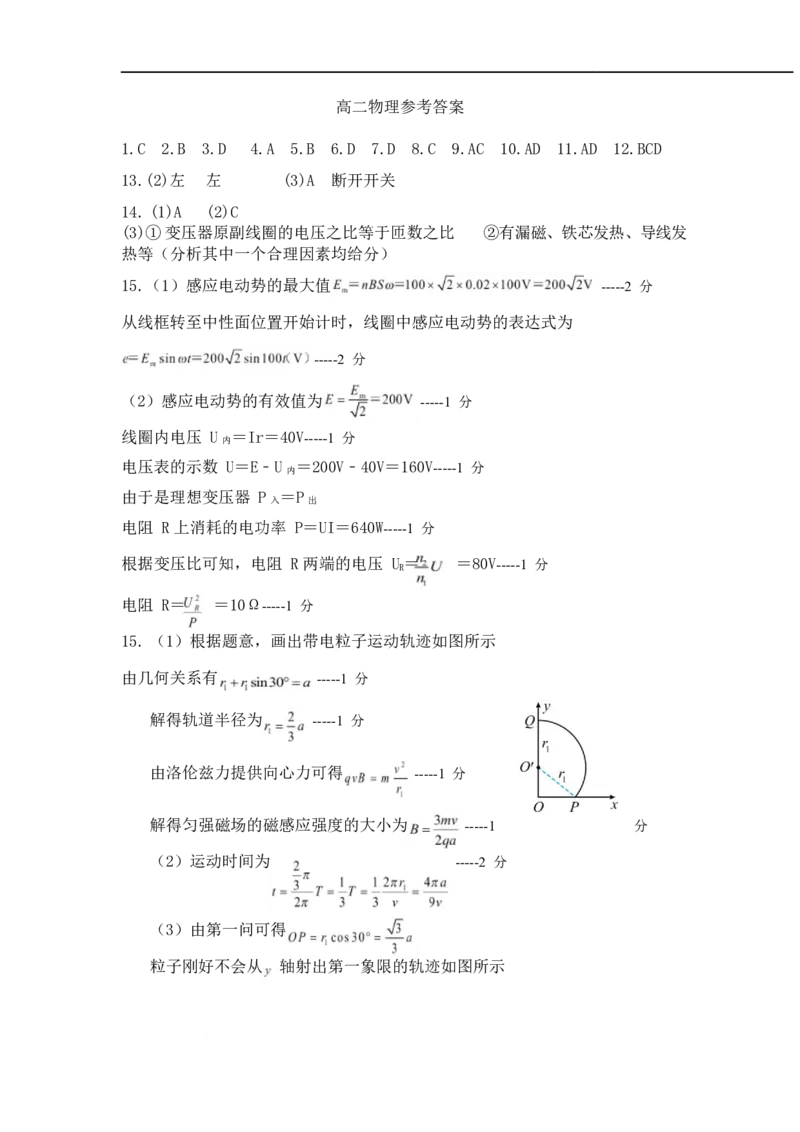
15. (1)根据题意,画出带电粒子运动轨迹如图所示
由几何关系有 -----1 分
解得轨道半径为 -----1 分
由洛伦兹力提供向心力可得 -----1 分
解得匀强磁场的磁感应强度的大小为 -----1 分
(2)运动时间为 -----2 分
(3)由第一问可得
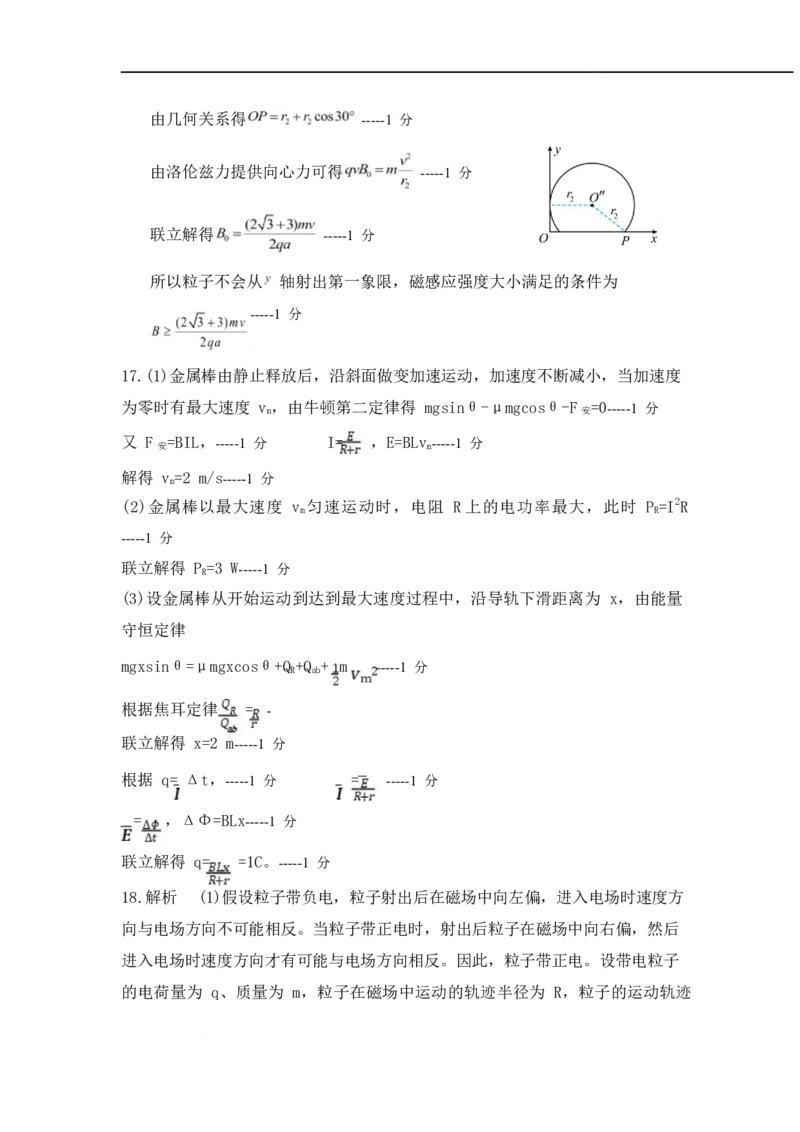
粒子刚好不会从 轴射出第一象限的轨迹如图所示由几何关系得 -----1 分
由洛伦兹力提供向心力可得 -----1 分
联立解得 -----1 分
所以粒子不会从 轴射出第一象限,磁感应强度大小满足的条件为
-----1 分
17.(1)金属棒由静止释放后,沿斜面做变加速运动,加速度不断减小,当加速度
为零时有最大速度 v
m
,由牛顿第二定律得 mgsinθ-μmgcosθ-F
安
=0-----1 分
又 F 安 =BIL,-----1 分 I= ,E=BLv m-----1 分
解得 v
m
=2 m/s-----1 分
(2)金属棒以最大速度 v 匀速运动时,电阻 R 上的电功率最大,此时 P =I2R
m R
-----1 分
联立解得 P
R
=3 W-----1 分
(3)设金属棒从开始运动到达到最大速度过程中,沿导轨下滑距离为 x,由能量
守恒定律
mgxsinθ=μmgxcosθ+Q R +Q ab + m -----1 分
根据焦耳定律 = -
联立解得 x=2 m-----1 分
根据 q= Δt,-----1 分 = -----1 分
= ,ΔΦ=BLx-----1 分
联立解得 q= =1C。-----1 分
18.解析 (1)假设粒子带负电,粒子射出后在磁场中向左偏,进入电场时速度方
向与电场方向不可能相反。当粒子带正电时,射出后粒子在磁场中向右偏,然后
进入电场时速度方向才有可能与电场方向相反。因此,粒子带正电。设带电粒子
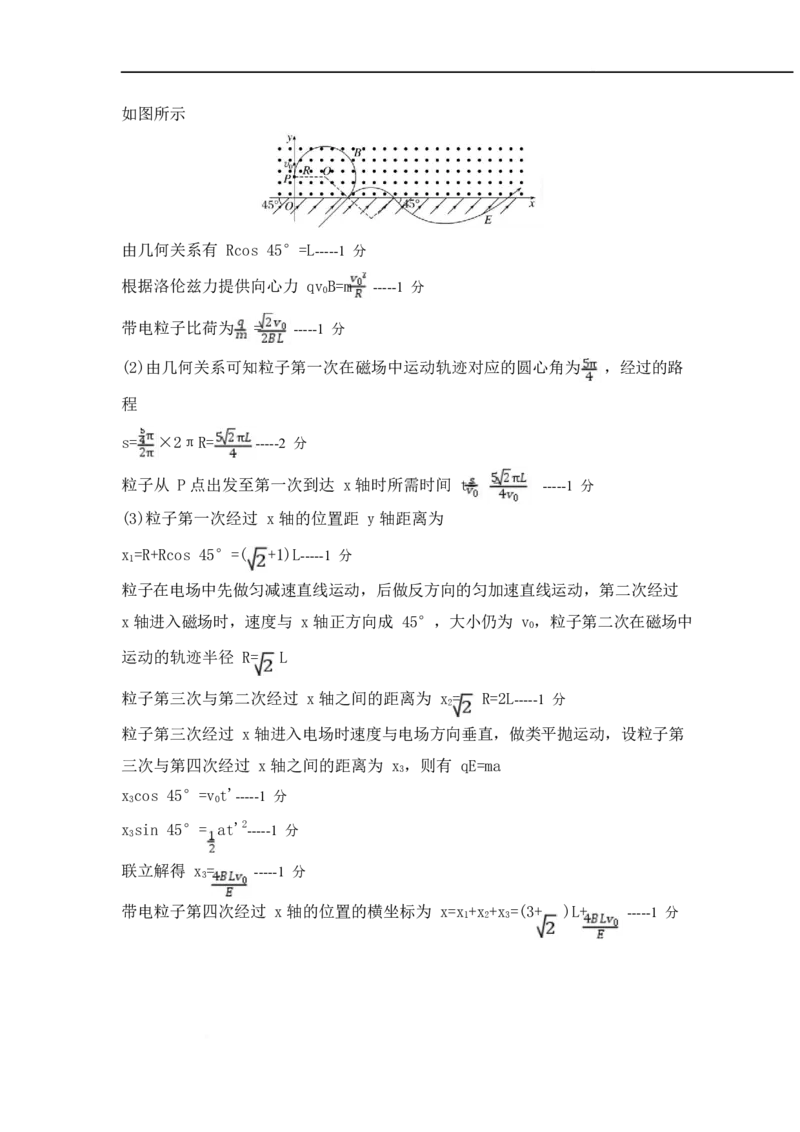
的电荷量为 q、质量为 m,粒子在磁场中运动的轨迹半径为 R,粒子的运动轨迹如图所示
由几何关系有 Rcos 45°=L-----1 分
根据洛伦兹力提供向心力 qv 0 B=m -----1 分
带电粒子比荷为 = -----1 分
(2)由几何关系可知粒子第一次在磁场中运动轨迹对应的圆心角为 ,经过的路
程
s= ×2πR= -----2 分
粒子从 P 点出发至第一次到达 x 轴时所需时间 t= = -----1 分
(3)粒子第一次经过 x 轴的位置距 y 轴距离为
x
1
=R+Rcos 45°=( +1)L-----1 分
粒子在电场中先做匀减速直线运动,后做反方向的匀加速直线运动,第二次经过
x 轴进入磁场时,速度与 x 轴正方向成 45°,大小仍为 v ,粒子第二次在磁场中
0
运动的轨迹半径 R= L
粒子第三次与第二次经过 x 轴之间的距离为 x
2
= R=2L-----1 分
粒子第三次经过 x 轴进入电场时速度与电场方向垂直,做类平抛运动,设粒子第
三次与第四次经过 x 轴之间的距离为 x ,则有 qE=ma
3
x
3
cos 45°=v
0
t'-----1 分
x 3 sin 45°= at'2 -----1 分
联立解得 x 3 = -----1 分
带电粒子第四次经过 x 轴的位置的横坐标为 x=x 1 +x 2 +x 3 =(3+ )L+ -----1 分